多头注意力，自注意力和位置编码
🔍 一、多头注意力的核心思想
多头注意力的目的是：
让模型从不同的表示子空间中学习到输入序列的不同行为，并将这些行为组合起来，从而捕获更丰富的依赖关系（如短距离、长距离依赖等）。
换句话说，就是 “从多个角度看问题”，然后把各个视角的结果融合起来，形成更全面的理解。
🧱 二、多头注意力的工作流程
- 线性变换：对原始查询（Query）、键（Key）、值（Value）分别进行 \(h\) 组不同的线性投影。
- 并行计算：每组变换后的 QKV 输入到一个独立的注意力头中，得到一个注意力输出。
- 拼接输出：将所有 \(h\) 个头的输出拼接在一起。
- 最终线性变换：通过一个新的线性层，将拼接后的结果映射成最终输出。
📐 三、数学形式化描述
给定：
- 查询 \(\mathbf{q} \in \mathbb{R}^{d_q}\)
- 键 \(\mathbf{k} \in \mathbb{R}^{d_k}\)
- 值 \(\mathbf{v} \in \mathbb{R}^{d_v}\)
每个注意力头 \(i = 1, ..., h\) 的计算为：
\[\mathbf{h}_i = f(\mathbf{W}_i^{(q)}\mathbf{q},\ \mathbf{W}_i^{(k)}\mathbf{k},\ \mathbf{W}_i^{(v)}\mathbf{v}) \in \mathbb{R}^{p_v}
\]
其中：
- \(\mathbf{W}_i^{(q)} \in \mathbb{R}^{p_q \times d_q}\)：查询的投影矩阵
- \(\mathbf{W}_i^{(k)} \in \mathbb{R}^{p_k \times d_k}\)：键的投影矩阵
- \(\mathbf{W}_i^{(v)} \in \mathbb{R}^{p_v \times d_v}\)：值的投影矩阵
- \(f\) 是注意力汇聚函数（如缩放点积注意力）
最后将所有头的输出拼接并通过一个线性变换：
\[\text{MultiHead}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \mathbf{W}_o
\begin{bmatrix}
\mathbf{h}_1 \\
\vdots \\
\mathbf{h}_h
\end{bmatrix}
\in \mathbb{R}^{p_o}
\]
其中：
- \(\mathbf{W}_o \in \mathbb{R}^{p_o \times h p_v}\)：最终的输出线性变换矩阵
🎯 四、关键优势
| 优点 | 说明 |
|---|---|
| 捕捉多种依赖关系 | 每个头可以关注序列中不同位置或不同粒度的信息，例如有的头关注局部信息，有的关注全局信息。 |
| 增强模型表达能力 | 多个头的组合比单一头具有更强的建模能力。 |
| 参数效率高 | 所有头共享相同的输入特征，但使用不同的投影权重，避免了重复提取特征。 |
| 并行性强 | 每个头之间是并行处理的，适合 GPU 加速。 |
🖼️ 五、图示理解
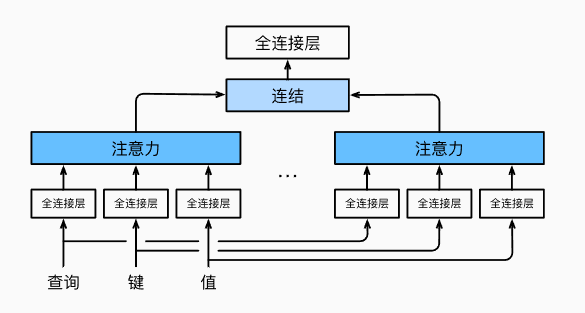
上图展示了：
- 输入的 Query、Key、Value 分别被 \(h\) 个不同的全连接层（线性变换）映射到不同的子空间。
- 每一组变换后的 QKV 被送入一个注意力头。
- 所有头的输出被拼接后，再经过一个线性层输出最终结果。
🧠 六、实际应用（Transformer）
在 Transformer 中，多头注意力模块广泛应用于：
- 编码器中的自注意力（Self-Attention）
- 解码器中的掩码自注意力和编码器-解码器注意力
- 每个头通常使用缩放点积注意力（Scaled Dot-Product Attention）
实现
在实现过程中通常选择缩放点积注意力作为每一个注意力头。
为了避免计算代价和参数代价的大幅增长，
我们设定\(p_q = p_k = p_v = p_o / h\)。
值得注意的是，如果将查询、键和值的线性变换的输出数量设置为
\(p_q h = p_k h = p_v h = p_o\)，
则可以并行计算\(h\)个头。
在下面的实现中，\(p_o\)是通过参数num_hiddens指定的。
import math
import torch
from torch import nn
from d2l import torch as d2l
class MultiHeadAttention(nn.Module):
"""多头注意力"""
def __init__(self, key_size, query_size, value_size, num_hiddens,
num_heads, dropout, bias=False, **kwargs):
super(MultiHeadAttention, self).__init__(**kwargs)
self.num_heads = num_heads
self.attention = d2l.DotProductAttention(dropout)
self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)
## 我们已经假定了q_featrues_all_heads = k_featrues_all_heads = v_featrues_all_heads = num_hiddens = out_featrues
## 同时我们还假定 q_featrues_each_head = k_featrues_each_head = v_featrues_each_head = num_hiddens/num_head = out_featrue/num_head(即out_featrue_each_head)
self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)
self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias) ## out_featrue应该等于v_featrues_all_head = num_head * v_featrues_each_head = num_hiddens,正是我们的假定
def forward(self, queries, keys, values, valid_lens):
# queries，keys，values的形状:
# (batch_size，查询或者“键－值”对的个数，num_hiddens)
# valid_lens 的形状:
# (batch_size，)或(batch_size，查询的个数)
queries = transpose_qkv(self.W_q(queries), self.num_heads)
keys = transpose_qkv(self.W_k(keys), self.num_heads)
values = transpose_qkv(self.W_v(values), self.num_heads)
# 经过变换后，输出的queries，keys，values 的形状:
# (batch_size*num_heads，查询或者“键－值”对的个数，num_hiddens/num_heads)
if valid_lens is not None:
# 在轴0，将第一项（标量或者矢量）复制num_heads次，
# 然后如此复制第二项，然后诸如此类。
valid_lens = torch.repeat_interleave(
valid_lens, repeats=self.num_heads, dim=0)
# output的形状:(batch_size*num_heads，查询的个数，num_hiddens/num_heads)
output = self.attention(queries, keys, values, valid_lens)
# output_concat的形状:(batch_size，查询的个数，num_hiddens)
output_concat = transpose_output(output, self.num_heads)
return self.W_o(output_concat)
def transpose_qkv(X, num_heads):
"""为了多注意力头的并行计算而变换形状"""
# 输入X的形状:(batch_size，查询或者“键－值”对的个数，num_hiddens)
X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)
# 输出X的形状:(batch_size，查询或者“键－值”对的个数，num_heads，num_hiddens/num_heads)
X = X.permute(0, 2, 1, 3)
# 输出X的形状:(batch_size，num_heads，查询或者“键－值”对的个数, num_hiddens/num_heads)
return X.reshape(-1, X.shape[2], X.shape[3])
# 最终输出的形状:(batch_size*num_heads,查询或者“键－值”对的个数, num_hiddens/num_heads)
def transpose_output(X, num_heads):
"""逆转transpose_qkv函数的操作"""
X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
X = X.permute(0, 2, 1, 3)
return X.reshape(X.shape[0], X.shape[1], -1)
自注意力机制（Self-Attention）
-
定义：自注意力是一种特殊的注意力机制，在这种机制下，查询（Query）、键（Key）和值（Value）都来自同一组输入序列。每个词元的表示通过考虑整个序列中的所有其他词元的信息来更新。
-
计算过程：
- 输入是一个词元序列\(\mathbf{x}_1, \ldots, \mathbf{x}_n\)，其中每个\(\mathbf{x}_i \in \mathbb{R}^d\)。
- 对于每个词元\(\mathbf{x}_i\)，计算其新的表示\(\mathbf{y}_i\)，该表示是基于整个序列的信息生成的，即\(\mathbf{y}_i = f(\mathbf{x}_i, (\mathbf{x}_1, \mathbf{x}_1), \ldots, (\mathbf{x}_n, \mathbf{x}_n))\)。这里\(f\)代表注意力汇聚函数。
- 这个过程允许模型在生成每个输出词元时关注到输入序列中的所有词元，从而能够捕捉复杂的模式和依赖关系。
下面的代码片段是基于多头注意力对一个张量完成自注意力的计算，张量的形状为（批量大小，时间步的数目或词元序列的长度，\(d\)）。
输出与输入的张量形状相同。
num_hiddens, num_heads = 100, 5
attention = d2l.MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,
num_hiddens, num_heads, 0.5)
attention.eval()
# 输出为：
# MultiHeadAttention(
# (attention): DotProductAttention(
# (dropout): Dropout(p=0.5, inplace=False)
# )
# (W_q): Linear(in_features=100, out_features=100, bias=False)
# (W_k): Linear(in_features=100, out_features=100, bias=False)
# (W_v): Linear(in_features=100, out_features=100, bias=False)
# (W_o): Linear(in_features=100, out_features=100, bias=False)
# )
batch_size, num_queries, valid_lens = 2, 4, torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens))
attention(X, X, X, valid_lens).shape
# 输出为：
# torch.Size([2, 4, 100])
位置编码（Positional Encoding）
-
必要性：由于自注意力机制本身不区分输入词元的顺序，因此需要额外的方法来注入顺序信息。这就是位置编码的作用。
-
实现方式：
- 可以通过添加一个与输入嵌入维度相同的向量\(\mathbf{P}\)来实现，这个向量根据词元在序列中的位置而变化。
- 有两种主要的位置编码方法：
- 可学习的位置编码：作为模型参数进行训练。
- 固定的位置编码：如原始Transformer论文中提出的基于正弦和余弦函数的方法，它不需要训练，但可以有效地给模型提供关于词元绝对位置的信息。
固定位置编码（基于正余弦函数的编码）
假设输入表示\(\mathbf{X} \in \mathbb{R}^{n \times d}\)包含一个序列中\(n\)个词元的\(d\)维嵌入表示。位置编码使用相同形状的位置嵌入矩阵
\(\mathbf{P} \in \mathbb{R}^{n \times d}\)输出\(\mathbf{X} + \mathbf{P}\)，
矩阵第\(i\)行、第\(2j\)列和\(2j+1\)列上的元素为：
\[\begin{aligned} p_{i, 2j} &= \sin\left(\frac{i}{10000^{2j/d}}\right),\\p_{i, 2j+1} &= \cos\left(\frac{i}{10000^{2j/d}}\right).\end{aligned}
\]
乍一看，这种基于三角函数的设计看起来很奇怪。
在解释这个设计之前，让我们先在下面的PositionalEncoding类中实现它。
#@save
class PositionalEncoding(nn.Module):
"""位置编码"""
def __init__(self, num_hiddens, dropout, max_len=1000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(dropout)
# 创建一个足够长的P
self.P = torch.zeros((1, max_len, num_hiddens))
X = torch.arange(max_len, dtype=torch.float32).reshape(
-1, 1) / torch.pow(10000, torch.arange(
0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)
self.P[:, :, 0::2] = torch.sin(X) # p[:, :, 0::2] 前两个维度表示取全部维度，最后一个维度表示从0开始一直取，步长为2
self.P[:, :, 1::2] = torch.cos(X)
def forward(self, X):
## x.shape = [batch_size, num_step, featrues],
## p.shape = [1, max_len, featrues]
X = X + self.P[:, :X.shape[1], :].to(X.device) ## 这里截断加广播，p的维度变成和x一样，再加到x上
return self.dropout(X)
在位置嵌入矩阵\(\mathbf{P}\)中，
[行代表词元在序列中的位置，列代表位置编码的不同维度]。
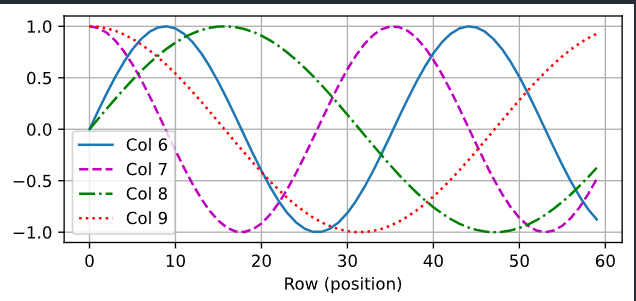
从下面的例子中可以看到位置嵌入矩阵的第\(6\)列和第\(7\)列的频率高于第\(8\)列和第\(9\)列。
第\(6\)列和第\(7\)列之间的偏移量（第\(8\)列和第\(9\)列相同）是由于正弦函数和余弦函数的交替。
encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
pos_encoding.eval()
X = pos_encoding(torch.zeros((1, num_steps, encoding_dim)))
P = pos_encoding.P[:, :X.shape[1], :]
d2l.plot(torch.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',
figsize=(6, 2.5), legend=["Col %d" % d for d in torch.arange(6, 10)])
绝对位置信息
为了明白沿着编码维度单调降低的频率与绝对位置信息的关系，
让我们打印出\(0, 1, \ldots, 7\)的[二进制表示]形式。
正如所看到的，每个数字、每两个数字和每四个数字上的比特值
在第一个最低位、第二个最低位和第三个最低位上分别交替。
for i in range(8):
print(f'{i}的二进制是：{i:>03b}')
# 结果如下
# 0的二进制是：000
# 1的二进制是：001
# 2的二进制是：010
# 3的二进制是：011
# 4的二进制是：100
# 5的二进制是：101
# 6的二进制是：110
# 7的二进制是：111
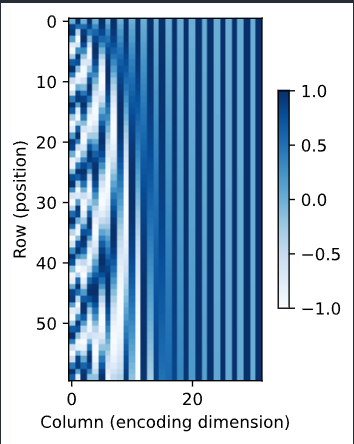
在二进制表示中，较高比特位的交替频率低于较低比特位，
与下面的热图所示相似，只是位置编码通过使用三角函数[在编码维度上降低频率]。
由于输出是浮点数，因此此类连续表示比二进制表示法更节省空间。
P = P[0, :, :].unsqueeze(0).unsqueeze(0)
d2l.show_heatmaps(P, xlabel='Column (encoding dimension)',
ylabel='Row (position)', figsize=(3.5, 4), cmap='Blues')
相对位置信息
位置编码的设计使得模型不仅能够捕捉绝对位置信息，还能学习到相对位置信息。具体来说：
对于任何确定的位置偏移 \(\delta\)，位置 \(i + \delta\) 处的位置编码可以通过对位置 \(i\) 处的位置编码进行线性投影来表示。这种关系可以通过以下数学推导说明：
假设 \(\omega_j = 1 / 10000^{2j/d}\)，则对于任意确定的位置偏移 \(\delta\)，位置 \((p_{i, 2j}, p_{i, 2j+1})\) 可以通过以下线性变换投影到 \((p_{i+\delta, 2j}, p_{i+\delta, 2j+1})\)：
\[\begin{aligned}
&\begin{bmatrix}
\cos(\delta \omega_j) & \sin(\delta \omega_j) \\
-\sin(\delta \omega_j) & \cos(\delta \omega_j)
\end{bmatrix}
\begin{bmatrix}
p_{i, 2j} \\
p_{i, 2j+1}
\end{bmatrix}\\
=&\begin{bmatrix}
\cos(\delta \omega_j) \sin(i \omega_j) + \sin(\delta \omega_j) \cos(i \omega_j) \\
-\sin(\delta \omega_j) \sin(i \omega_j) + \cos(\delta \omega_j) \cos(i \omega_j)
\end{bmatrix}\\
=&\begin{bmatrix}
\sin((i+\delta) \omega_j) \\
\cos((i+\delta) \omega_j)
\end{bmatrix}\\
=&
\begin{bmatrix}
p_{i+\delta, 2j} \\
p_{i+\delta, 2j+1}
\end{bmatrix},
\end{aligned}
\]
这个推导表明：
- 对于每个维度 \(j\)，位置 \(i\) 和位置 \(i + \delta\) 的位置编码之间存在一种旋转关系。
- 这种旋转关系由一个 \(2 \times 2\) 的旋转矩阵决定，该矩阵不依赖于具体的索引 \(i\)。
浙公网安备 33010602011771号