【题目】ccf csp 202309-3 梯队求解

题目大意：给出需要求解的逆波兰表达式（后缀表达式），包含多个变量，现在每一次查询，给出所有变量的值，询问对于给定的变量其函数偏导值为多少。（仅包含乘、加减运算）

（例如，对于表达式：

x1 x1 x1 * x2 + *

可转化为(x1 * x1 + x2) * x1

对x1求偏导后变为(2 * x1 + x2) + (x1 * x1 + x2)

带入x1 = 2，x2 = 3可以得到 (2 * 2 + 3) + (2 * 2 + 3) = 7 + 7 = 14）

考虑递归迭代地解决问题，我们把表达式视为一棵树，我们得到了一个根结点为运算，叶子结点为常数或变量的二叉树。

例如，上式可化作：

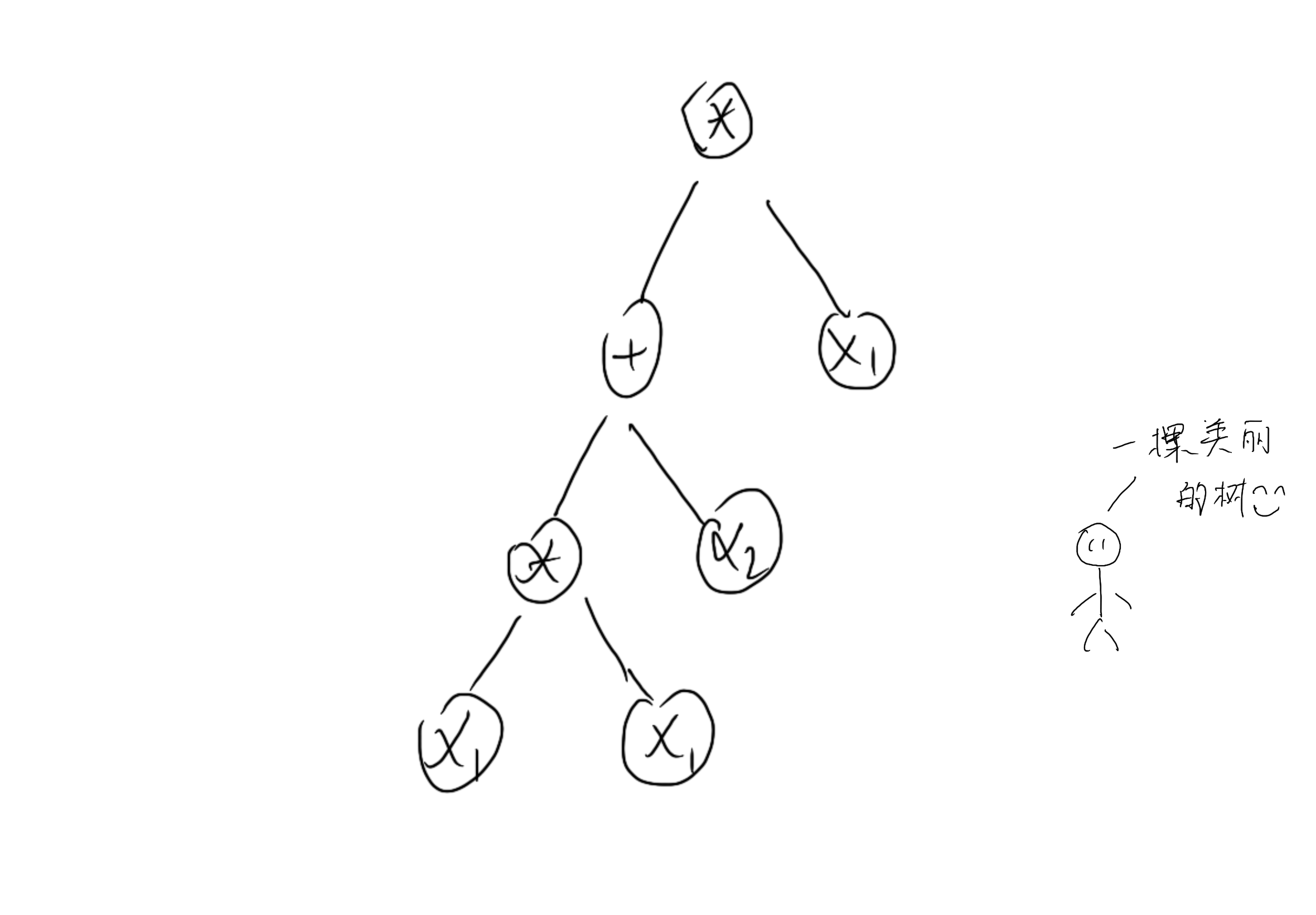
我们敏锐地发现，如果按照平常的习惯，从上往下遍历这棵树来求导，仅有乘法会需要下一层的两种运算法则的结果：原始计算结果和求导计算结果。

考虑到，直接存储求导后的表达式显然是不现实的，我们的目标是通过仅存储数值来完成两种运算。因此，我们对每个节点设置两个值：原始计算结果和求导计算结果。这样，每当遇到乘法节点t，设其儿子分别为s1，s2，求导结果为div，原始结果为ori，可以得到

t.div = s1.div * s2.ori + s1.ori * s2.div

t.ori = s1.ori * s2.ori

这里仅仅表述了最复杂的乘法节点如何计算。对于叶子节点l，若为自变量则l.div = 1, l.ori = value。

因此，根据后缀表达式从下向上处理每个节点，最终能得到每个节点所代表的子树的求导和原始结果。

AC代码：

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <cstdlib>

#define up(l,r,i) for(int i=l;i<=r;i++)
#define dn(l,r,i) for(int i=r;i>=l;i--)

#define ll long long

using namespace std;

const int MAXN = 130, MAXM = 102;
const int MOD = 1e9+7;

int n,m;

string str;

ll stacK[MAXN][2];//0 ori 1 div
int scnt;

int nums[MAXN];

int x;

void push(int a,int b){
    stacK[++scnt][0] = a;
    stacK[scnt][1] = b;
}



void solve(){

    up(0,str.size(),i){
        if(str[i] == ' '){continue;}
        else if(str[i] == 'x'){
            int cnt = 0;
            while(str[i+1+cnt] != ' ')
                cnt++;
            int  num = atoi(str.substr(i+1,cnt).c_str());
            i += cnt+1;
            push(nums[num],(x==num)?1:0);
            //cout<<"x"<<num<<endl;
        }
        else if(str[i] == '*'){
            ll a = stacK[scnt][0];
            ll b = stacK[scnt--][1];
            ll c = stacK[scnt][0];
            ll d = stacK[scnt--][1];
            push((a*c)%MOD,((a*d)%MOD + (b*c)%MOD)%MOD);
        }
        else if(str[i] == '+'){
            ll a = stacK[scnt][0];
            ll b = stacK[scnt--][1];
            ll c = stacK[scnt][0];
            ll d = stacK[scnt--][1];
            push((a + c)%MOD,(b + d)%MOD);
        }
        else if(str[i] == '-'){
            if(str[i+1] == ' '){
                ll a = stacK[scnt][0];
                ll b = stacK[scnt--][1];
                ll c = stacK[scnt][0];
                ll d = stacK[scnt--][1];
                push((c - a)%MOD,(d - b)%MOD);
            }
            else{
                int cnt = 0;
                while(str[i+1+cnt] != ' ') cnt++;
                ll num = atoi(str.substr(i,cnt+1).c_str());
                i += cnt+1;
                //cout<<"-n"<<num<<endl;
                push(num,0);
            }
        }
        else if('0' <= str[i] && str[i] <= '9'){
            int cnt = 0;
            while(str[i+cnt] != ' ') cnt++;
            ll num = atoi(str.substr(i,cnt).c_str());
            i += cnt;
            push(num,0);
            //cout<<"n"<<num<<endl;
        }

    }
}


int main()
{
    cin>>n>>m; 
    getchar();
    str.resize(1000);
    getline(cin, str);
    str += ' ';

    up(1,m,ii){
        cin>>x;
        up(1,n,i)
            cin>>nums[i];
        scnt = 0;
        solve();
        if(stacK[1][1] < 0) stacK[1][1] += MOD;
        cout<<stacK[1][1]<<endl;
    }

    return 0;
}