07-格与布尔代数

格的基本概念

设\(<A, \leq>\)是一个偏序集，对\(\forall a,b \in A\), 子集{a,b}在A中都有最大下界（下确界）和最小上界（上确界），则称\(<A, \leq>\)为格。

根据上确界和下确界的唯一性， 可以把求{a,b}的上确界，和下确界看作是a与b的二元运算。\(下确界：a \and b\) \(上确界a： \or b\)

---

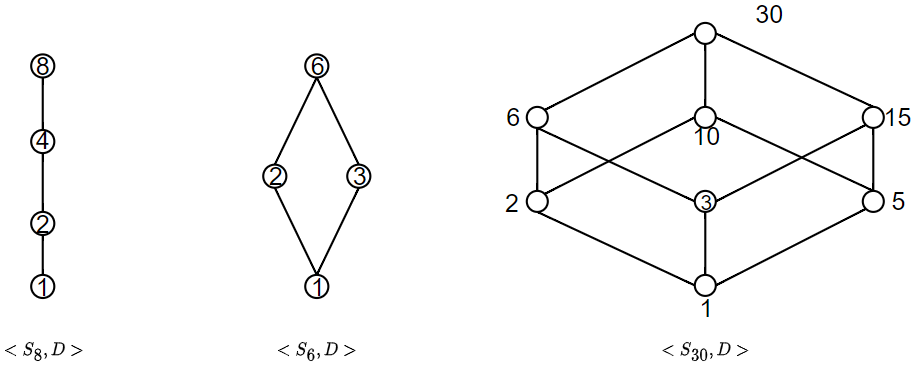
设n是正整数， \(S_n\)是n的正因子集合。 D为整除关系。则偏序集\(<S_n, D>\)构成格。

• \(\forall x,y \in S_n, x \or y 是 Icm(x,y)即x与y的最小公倍数。\)
• \(\forall x,y \in S_n, x \and y 是 gcd(x,y)即x与y的最大公倍数。\)

这四个都不是格

• a中， {a,b}没有下确界
• b中， {c,e}没有下确界（b=d, 没有最小）
• c中， {a,f}没有上确界和下确界 （d=e, b=c， 没有最小）
• d中， 没有关系

对偶命题

设\(<A, \leq>\)是一个格，如果在A上定义两个二元运算\(\and 和 \or\)， 使得\(\forall a,b \in A, a \and b 等于a和b的最大下界， a \or b 等于a和b的最小上界。\)称\(<A,\and,\or>\)为由格\(<A,\leq>\)所诱导的代数系统。二元运算分别称为交运算和并运算。

设\(<S, \leq>\)是一个格,P是由格中元素及\(\leq, = , \geq, \and , \or\)等符号表示的命题，如果将P中的\(\leq\)替换为\(\geq\), \(\geq\)替换为\(\leq\), \(\and\)替换为\(\or\), \(\or\)替换为\(\and\) 得到的命题\(P^{'}\)称为P的对偶命题。

• 若\(P=a\and b \leq a = a\), 其对偶命题\(P^{'}=a \or b \geq a = a\)

格的对偶原理：如果命题P对一切格L为真， 则P的对偶命题也对一切格为真

• 全序集都是格， 但偏序集不一定全都是格

格的性质

设\(<L, \leq>\)是一个格，则运算 \(\and 和 \or\) 适合交换律、结合律、幂等律、吸收律，即：

• \(\forall a,b \in L 有： a\or b = b \or a, a\and b = b \and a\)
• \(\forall a,b,c \in L 有：(a\or b)\or c= a\or (b\or c), (a \and b) \and c = a \and (b \and c)\)
• \(\forall a \in L 有：a\or a = a , a \and a = a\)
• \(\forall a,b \in L 有：a \or(a\and b) = a, a \and (a \or b)=a\)

在一个格\(<A, \leq>\)中，对\(\forall a,b \in A\)都有：

• \(a \leq a\or b\)，\(b \leq a\or b\), \(a \geq a \and b\), \(b \geq a \and b\)
• 由对偶原理，反之亦然

设\(<S,*,\circ>\)是一个具有两个二元运算的代数系统，若对于\(*\) 和 \(\circ\)运算适合交换律、结合律、幂等律、吸收律，则S上存在偏序关系 \(\leq\) 使得\(<S, \leq>\)是一个格, 且\(\forall a,b \in A有：a \and b = a*b, a\or b = a \circ b\)

设\(<L,\and,\or>\)是代数系统，其中\(\and\), \(\or\)是二元运算， 若\(\and\), \(\or\)满足交换律、结合律、吸收律，则称\(<L,\and,\or>\)是一个格。

分配格与有补格

格的运算满足交换律、结合律、吸收律已经幂等律，但不是所有格都满足分配律。满足分配律的格成为一类特殊的格。

分配格

设\(<L,\and,\or>\)是格， 若\(\forall a,b,c \in L\)有 \(a \and (b \or c) = (a \and b ) \or (a \and c)\) 或 \(a \or (b \and c) = (a \or b ) \and (a \or c)\) ，则称L为分配格。

以上条件互为充分必要条件，在证明L是分配格时，只须要证明其中一个等式即可。

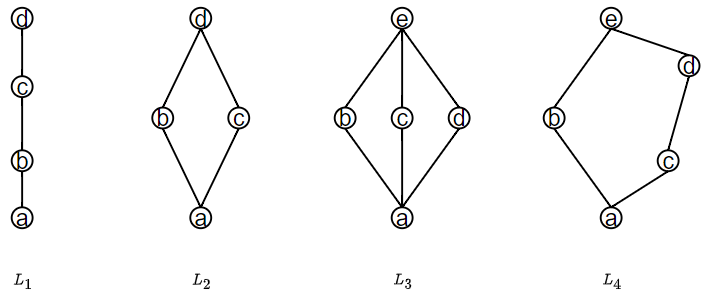
\(L_1, L_2\)是分配格， \(L_3(钻石格),L_4(五角格)\)不是分配格。

L3, \(b\and(c \or d)=b, (b \and c)\or (b \and d)=a\) 不满足分配律

L4, \(c \or (b \and d)=c, (c \or b) \and (c \or d)=d\) 不满足分配律

设L是格， 则L是分配格当且仅当L不含有与钻石格或五角格同构的子格。

• 小于五元的格都是分配格
• 任何一条链路都是分配格

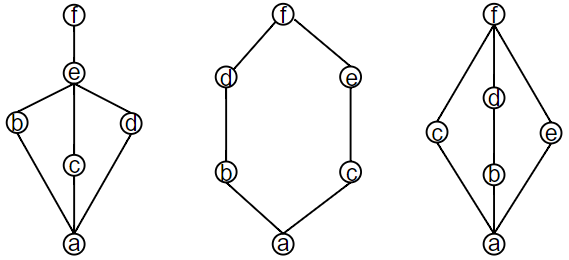
上述都不是分配格。 它们是钻石格或五角格的子格。

有补格

设\(<A,\leq>\)是一个格，

• 如果存在元素\(a \in A\)对于\(\forall x \in A\) 都有 \(a \leq x\) 称a为格的全下界；全下界是最小元， 记为0

• 如果存在元素\(b \in A\)对于\(\forall x \in A\) 都有 \(x \leq b\) 称b为格的全上界；全上界是最大元 ，记为1

• 若A存在全下界和权上界，则称A为有界格，记作\(<A,\and,\or,0,1>\)

补元

设\(<A,∧,∨,0,1>\)是有界格， \(a \in A\) 若存在 \(b \in A\) 使得 \(a\or b = 1\) 且 \(a \and b = 0\) 称b是a的补元。

• a是b的补元，则b也是a的补元，简称互补
• 任何有界格中，全下界和全上界总是互补的；其他元素可能存在补元，补元可能不唯一
• 对于有界分配格，它的元素如果存在补元则一定唯一
• a的补元记作\(a^{'}或\bar{a}\)

设\(<A,∧,∨,0,1>\)是有界分配格， 若\(a \in A\)，且对于a存在补元b， 则b是a的唯一补元。

有补格

设\(<A,∧,∨,0,1>\)是有界格， 若对于\(\forall a \in A\), 在A中都有a的补元存在， 则称A为有补格。

布尔代数

如果一个格是有补分配格， 则称它为布尔格或布尔代数。

• 如果一个元素存在补元，则是唯一的

设有代数系统\(<B, \and , \or , ',0,1>\), 其中B至少包含2个元素， \(\and , \or\) 是二元运算， \('\) 是一元运算。则对 \(\forall a,b,c \in B\) 满足：

1. \(a \and b = b \and a, a\or b = b \or a\)
2. \(a \and (b \or c)= (a \and b )\ or (a \and c), a \or (b \and c) = (a \or b) \and (a \or c)\)
3. 在B中存在零元0， 使\(a \or 0=a, a \and 0 =0\); 存在单位元1, 使\(a \and 1= a, a\or 1= 1\)
4. \(a^{'} \in B\) 使 \(a \and a^{'}=0, a \or a^{'}=1\)

则\(<B, \and , \or , ',0,1>\) 是布尔格。

设L是有限布尔代数， 则L含有\(2^n\)格元素(\(n \in Z\)）, 且L与\(<P(S), \cap, \cup,\empty, S>\)同构， 其中S是一个n元集合