04-集合
基本概念
- 集合是最基本的离散结构,是由一些个体组成的全体。
- 元素、成员:组成集合的个体
- 有穷集、有限集:由有限个元素组成;
- 无穷集、无限集:由无限个元素组成;
- 集合中的元素具有唯一性(元素不能重复出现),次序不重要
常用数集
| 符号 | 数集 | 符号 | 数集 |
|---|---|---|---|
| \(N\) | 自然数集合 | \(Z\) | 整数集合 |
| \(Q\) | 有理数集合 | \(Z^+\) | 正整数集 |
| \(R\) | 实数集合 | \(Q_-\) | 负有理数集 |
| \(C\) | 复数集合 | \(Q_+\) | 正有理数集 |
元素与集合的关系
-
属于:若元素a是集合A中的元素,则称a属于A, 记为 \(a\in A\), 否则称a不属于A, 记为 \(a \notin A\)
-
相等:若集合A与B含有相同的元素时,称A与B相等,记为\(A=B\), 否则称不相等,记为\(A\neq B\)
集合的基数、势
集合A中元素的个数称为集合的势或基数。表示为 \(|A|\)
有限集的基数为自然数,如果一个无限集合可以跟自然数集合形成一一对应,则称其为可数无限集,反之为不可数集合。
- 空集:不含有任何元素的集合称为空集,记为\(\empty\) 或 \(\{\}\);
集合的表示法
-
列举法
\(E=\{0,3,6,9...3n,...\}\)
\(\emptyset 空集\)
-
描述法
使用谓词来刻画集合元素的性质;谓词既可以使用自然语言,也可以使用形式语言。
\(S=\{x|P(x)\}\) 当P(b)为真时,b时S中的元素。
- 图示法
集合的关系
- 包含
- 设A、B为任意两个集合,若A中的每一个元素都属于B, 则称A为B的子集,也称B包含A, 或A包含在B内。 记作:\(A \subseteq B 或 B \supseteq A\)
- 真子集 \(\subset\) , 子集A中的每一个元素都属于集合B, 但是B中至少有一个元素不属于A
- 相等
- 任意两个集合A和B, A与B相等的充分必要条件是两个集合互为子集
- 空集
- 空集是任何集合的子集
- 幂集
- 集合中全部子集组成的集合
- A={a,b,{c}}
- \(\mathscr{P}(A)=\{\emptyset,\{a\},\{b\},\{\{c\}\},\{a,b\},\{a,\{c\}\}, \{b,\{c\}\},\{a,b,\{c\}\}\}\)
- 全集 \(E\)
- 在给定问题中,全集包含任何集合,即: \(\forall_A\subseteq E\)
- 基数、势
- 集合中元素的个数, 空集的势为0.
- A={1,2,3}, \(|A|=3\)
集合的基本运算
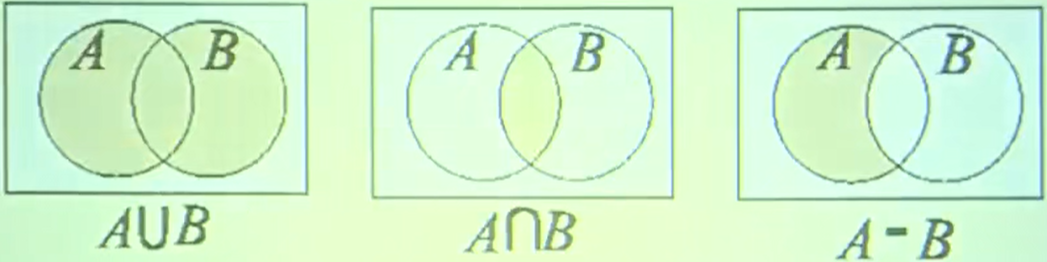
并
\(A\cup B = \{x | x \in A \or x \in B\}\)
交
$ A \cap B = {x | x \in A \and x \in B}$
差 相对补
\(A-B=\{x | x \in A \and x \notin B\}\) B对于A的补
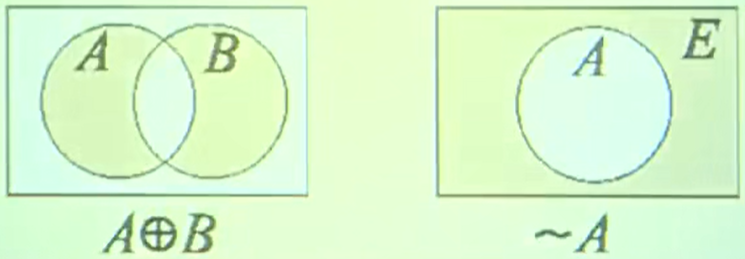
对称差
\(A \bigoplus B=(A-B)\cup (B-A)\)
\(A \bigoplus B=(A\cup B)- (A \cap B)\)
\(A \bigoplus B=\{x|(x \in A \or x \in B) \and (x \notin A \cap B)\} = \{x | x \in (A-B) \or x \in (B -A)\}\)
绝对补
\(\sim A=E -A\) A对于全集的补
集合运算的算律
| \(\cup\) | \(\cap\) | \(\bigoplus\) | |
|---|---|---|---|
| 交换 | \(A \cup B = B \cup A\) | \(A \cap B = B \cap A\) | \(A \bigoplus B = B \bigoplus A\) |
| 结合 | \((A \cup B) \cup C = A \cup (B \cup C)\) | \((A \cap B) \cap C= A \cap (B \cap C)\) | \((A \bigoplus B) \bigoplus C = A \bigoplus (B \bigoplus C)\) |
| 幂等 | \(A \cup A = A\) | \(A \cap A = A\) |
| \(\cup 与 \cap\) | \(\cap 与 \bigoplus\) | |
|---|---|---|
| 分配 | \(A \cup (B\cap C)= (A \cup B) \cap (A \cup C)\) \(A \cap (B\cup C)= (A \cap B) \cup (A \cap C)\) |
\(A \cap (B \bigoplus C)=(A \cap B)\bigoplus (A \cap C)\) |
| 吸收 | \(A \cup (A \cap B) = A\) \(A \cap (A \cup B) = A\) |
| \(\sim\) | ||
|---|---|---|
| 德摩根定律 | \(A-(B\cup C)=(A-B) \cap (A -C)\) \(A-(B\cap C)=(A -B) \cup (A-C)\) |
\(\sim(B \cup C) = \sim B \cap \sim C\) \(\sim(B \cap C)=\sim B \cup \sim C\) |
| 双重否定 | \(\sim\sim A = A\) |
| \(\emptyset\) | E | |
|---|---|---|
| 补元律 | \(A\cap \sim A=\emptyset\) | \(A\cup \sim A = E\) |
| 零律 | \(A \cap \emptyset = \emptyset\) | \(A \cup E = E\) |
| 同一律 | \(A \cup \emptyset = A\) | \(A\cap E = A\) |
| 否定 | \(\sim \emptyset = E\) | $\sim E = \emptyset $ |
\((A \cap B ) \cap C = A \cap (B \cap C)\)
证明
\[\begin{align} &\forall_x \in (A \cap B) \cap C \\ \Lrarr& x \in A \and x \in B \and x \in C \\ \Lrarr& x \in A \and x \in (B \cap C) \\ \Lrarr& x \in A \cap (B \cap C) \end{align} \]
对称差
集合A、B,A与B的对称差为集合S, S中元素或属于A或属于B,单不能既属于A又属于B。
\(A \bigoplus B=\{x|(x \in A \or x \in B) \and (x \notin A \cap B)\} = \{x | x \in (A-B) \or x \in (B -A)\}\)
有序对与笛卡尔乘积
由两个元素x,y按一定顺序排列而成的二元组称为一个有序对或序偶。记作\(<x,y> 或(x,y)\) x 是第一元素, y是第二元素
有序对中元素的顺序是重要的。 \(若x\neq y 则 <x,y> \neq <y,x>\)
设A、B为任意集合,A与B的笛卡尔积(直积)记作 \(A\times B\) 即: \(A\times B =\{ <x,y>| x\in A \and y \in B\}\)
- 对于任意集合A, \(A \times \empty = \empty; \;\; \empty \times A = \empty\)
- 笛卡尔积不满足交换律
- 笛卡尔积不满足结合律
- \(|A \times B | = |A| \times |B|\)
A={1,2,3}, B={a,b,c}
AxB={<1,a>, <1,b>, <1,c>, <2,a>, <2,b>, <2,c>, < 3,a>, < 3,b>, < 3,c>}
BxA={<a,1>, <b,1>, <c,1>, <a,2>, <b,2>, <c,2>, <a,3>, <b,3>, <c,3>}
|A x B| = m * n
\[\begin{align} & A \times (B \cup C) = (A\times B) \cup (A \times C) \\ & A \times (B \cap C) = (A\times B) \cap (A \times C) \\ & (A \cup B) \times C = (A\times C) \cup (B \times C) \\ & (A \cap B) \times C = (A\times C) \cap (B \times C) \\ \end{align} \]



 浙公网安备 33010602011771号
浙公网安备 33010602011771号