05-关系与函数

关系与关系的性质

关系的定义

A、B为两个集合， $A \times B$ 的子集R称为A到B的二元关系。

当A=B时，称R为A上的关系。

若$<x,y> \in R $ 可记为 $xRy$ 称x与y有关系

若$<x,y> \notin R$ 可记为 $x\textrecipe y$ 称x与y没有关系

关系是一个集合
关系是多个关系笛卡尔积的子集

特殊的关系：

全域关系、恒等关系、空关系

全域 $E_A=\{<x,y>|x \in A \and y \in A \}$
恒等 $I_A=\{<x,x>|x \in A\}$
空

R是集合A上的二元关系

关系的定义域

R中全体有序对的第一元素构成的集合称为R的定义域 $domR=\{x|\exist_y(<x,y> \in R)\}$

关系的值域

R中全体有序对的第二元素构成的集合称为R的值域 $ranR=\{y|\exist_x(<x,y> \in R)\}$

关系的域

R的定义域与值域的并集称为R的域。 $fldR=domR \cup ranR$

关系的表示方法

有序对集合
矩阵
关系图

矩阵

集合$X=\{x_1,x_2,...,x_n\}, Y=\{y_1,y_2,...,y_n\}$ R为X到Y的一个二元关系。称矩阵$M_R=(r_{ij})_{m\times n})$ 为对应于R的关系矩阵。

\[r_{ij}= \begin{cases} 1, 当 <x_i,y_j> \in R\\ 0, 当 <x_i,y_j> \notin R\\ \end{cases} \]
A={1,2,3}

R={<1,1>,<1,2>,<2,3>,❤️,3>}

\[M_R= \begin{Bmatrix} 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ \end{Bmatrix} \]

flowchart LR subgraph X x1((x1)) x2((x2)) x3((x3)) x4((x4)) end subgraph Y y1 y2 y3 y4 y5 end x1 --> y2 x1 --> y3 x2 --> y5 x3 --> y4 x4 --> y3

关系的性质

R是A上的二元关系

如果对 $\forall_a \in A$ 必有 $aRa$, 则称关系R在A上是自反的
如果对 $\forall_a \in A$ 必有 $a\textrecipe a$, 则称关系R在A上是反自反的
对 $\forall_a \;\;, b\in A$ 若 $aRb$ 必有 $ bRa$ 则称关系R在A上是对称的
对 $\forall_a \;\;, b\in A$ 若 $aRb$ 且 $ bRa$ 必有 $a=b$ 则称关系R在A上是反对称的（若$aRb且a\neq b$ 必有 $b\textrecipe a$）
对$\forall a,b,c \in A$ 若aRb且bRa 必有 aRc 则称关系R在A上是传递的 $(\forall<x,y>)(\forall<y,z)(<x,y> \in R \and <y,z> \in R \rarr <x,z> \in R)$

关系的性质中，自反相关的要判断A中的所有元素

关系的性质在关系矩阵与关系图中的特点

R是自反的，关系矩阵中对角线上所有元素都是1，关系图中每个顶点都有到自身的有向边（环）
R是反自反的，关系矩阵中对角线上所有元素都是0，关系图中每个顶点都没有到自身的有向边（环）
R是对称的，关系矩阵是对称矩阵，关系图上任何两个顶点间若存在有向边必是成对出现
R是反对称的，关系矩阵中以主对角线为对称的两个元素不能同时为1，在关系图上两个不同顶点间的有向边不会成对出现

关系	自反性	反自反性	对称性	反对称性	传递性
全域关系	☑️		☑️		☑️
恒等关系	☑️		☑️	☑️	☑️
空关系		☑️	☑️	☑️	☑️
小于等于关系	☑️			☑️	☑️
小于关系		☑️		☑️	☑️
整除关系	☑️			☑️	☑️

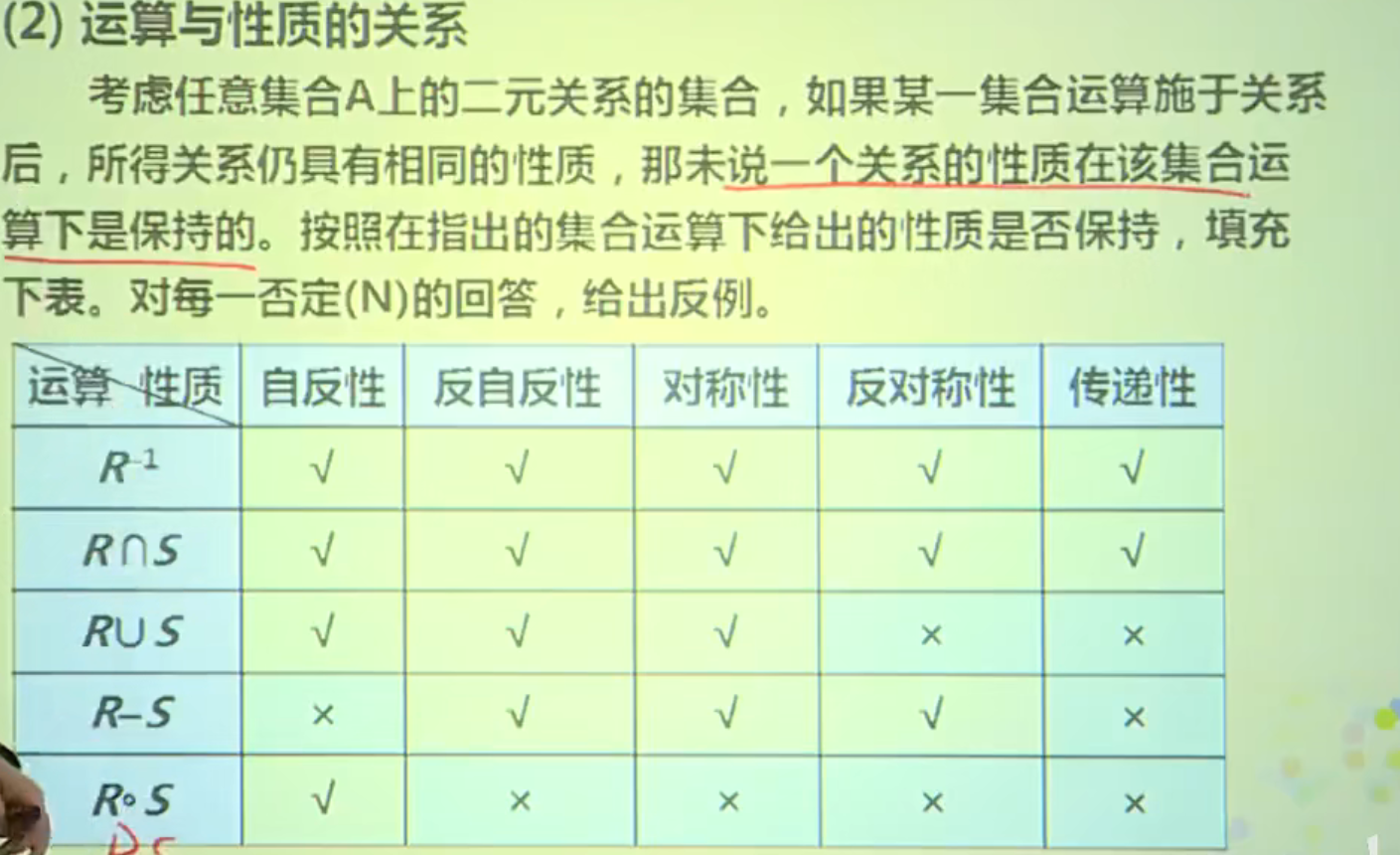
关系的运算

若Z和S是从集合X到Y的两个关系，则Z、S的并、叫、补、差仍是X到Y的关系

逆运算

设R是从X到Y的二元关系，如将R中每一个二元组中的元素顺序互换，所得到的集合称为R的逆关系，简称R的逆，记作 $R^{-1};; 或 ;;R^c $

即 $ R^{-1}={<y,x>|<x,y> \in R} $

设R、R1、R2 都是从A到B的二元关系，则以下公式成立

\[\begin{align} 1.&(R^{-1})^{-1}=R \\ 2.& (R_1\cup R_2)^{-1}=R_1^{-1} \cup R_2^{-1} \\ 3.& (R_1\cap R_2)^{-1}=R_1^{-1} \cap R_2^{-1} \\ 4.& (\tilde{R})^{-1} = \tilde{(R^{-1})}\\ 5.& (A\times B)^{-1}=B\times A\\ 6.& (R_1 - R_2)^{-1} = R_1^{-1} -R_2^{-1}\\ 7.& 若 R_1 \subseteq R_2 则 R_1^{-1} \subseteq R_2^{-1}\\ 8.& domR^{-1} = ranR\\ 9.& ranR^{-1} = domR\\ \end{align} \]
证明

\[\begin{align} 1.&(R^{-1})^{-1}=R \\ & \forall <a,b> \\ & <a,b> \in (R^{-1})^{-1} \\ & \Lrarr <b,a> R^{-1}\\ & \Lrarr <a,b> R \end{align} \]
\[\begin{align} 2.& (R_1\cup R_2)^{-1}=R_1^{-1} \cup R_2^{-1} \\ &\forall <a,b> \\ &<a,b> \in (R_1\cup R_2)^{-1} \\ &\Lrarr <b,a> \in (R_1\cup R_2) \\ &\Lrarr <b,a> \in R_1 \or <b,a> \in R_2 \\ &\Lrarr <a,b> \in R_1^{-1} \or <a,b> \in R_2^{-1} \\ &\Lrarr <a,b> \in R_1^{-1} \cup R_2^{-1} \\ \end{align} \]
\[\begin{align} 3.& (R_1\cap R_2)^{-1}=R_1^{-1} \cap R_2^{-1} \\ & \forall <a,b> \\ &\Lrarr <a,b> \in (R_1\cap R_2)^{-1}=R_1^{-1} \\ &\Lrarr <b,a> \in (R_1\cap R_2)\\ &\Lrarr <b,a> \in R_1 \and <b,a> \in R_2\\ &\Lrarr <a,b> \in R_1^{-1} \and <a,b> \in R_2^{-1}\\ &\Lrarr <a,b> \in R_1^{-1} \cap R_2^{-1} \end{align} \]
\[\begin{align} 4.& (\tilde{R})^{-1} = \tilde{(R^{-1})}\\ & \forall <a,b> \\ & <a,b> \in (\tilde{R})^{-1} \\ & \Lrarr <b,a> \in (\tilde{R}) \\ & \Lrarr <b,a> \notin R \\ & \Lrarr <a,b> \notin R^{-1} \\ & \Lrarr <a,b> \notin (\tilde{R^{-1}}) \\ \end{align} \]
\[\begin{align} 5.& (A\times B)^{-1}=B\times A\\ \end{align} \]
\[\begin{align} 6.& (R_1 - R_2)^{-1} = R_1^{-1} -R_2^{-1}\\ \end{align} \]
\[\begin{align} 7.& 若 R_1 \subseteq R_2 则 R_1^{-1} \subseteq R_2^{-1}\\ \end{align} \]
\[\begin{align} 8.& domR^{-1} = ranR\\ \end{align} \]
\[\begin{align} 9.& ranR^{-1} = domR\\ \end{align} \]

复合关系

设R是从A到B的二元关系，S是从B到C的二元关系

定义：$R\circ S = \{<x,z> | \exist_y(<x,y> \in R \and <y,z> \in S)\}$ 称为R和S的复合关系

设F是X到Y的关系， G是Y到Z的关系， H是Z到W的关系，则有：

$(F \circ G) \circ H = F \circ (G \circ H)$

\[\begin{align} &\forall <x,w> \\ <x,w> & \in (F \circ G) \circ H \\ \Lrarr & \exist_z(<x,z> \in F \circ G \and <z,w> \in H)\\ \Lrarr & \exist_z(\exist_y(<x,y> \in F \and <y,z> \in G) \and <z,w> \in H)\\ \Lrarr & \exist_y(<x,y> \in F \and \exist_z(<y,z> \in G \and <z,w> \in H)) \\ \Lrarr & \exist_y(<x,y> \in F \and <y,w> \in G \circ H)\\ \Lrarr & <x,w> \in F \circ (G \circ H) \end{align} \]

$(F \circ G)^{-1}=G^{-1} \circ F^{-1}$

\[\begin{align} \forall <x,z> \\ <x,z> &\in (F \circ G)^{-1} \\ \Lrarr &<z,x> \in F \circ G \\ \Lrarr & \exist_y(<z,y> \in F \and <y,x> \in G) \\ \Lrarr & \exist_y(<y,z> \in F^{-1} \and <x,y> \in G^{-1}) \\ \Lrarr & \exist_y(<x,y> \in G^{-1} \and <y,z> \in F^{-1}) \\ \Lrarr & <x,z> \in G^{-1} \and F^{-1} \end{align} \]

复合：第一个关系序偶中的第二元素是第二个关系中序号的第一元素，将第一个关系中序偶的第一元素与第二个关系中序偶的第二元素组合为新的序偶。

关系 R	关系 S	复合关系 $R \circ S$
<x,y>	<y,z>	<x,z>

R的n次幂

R是集合A上的关系，幂 $R^n(n=1,2,...)$ 递归地定义为$R^1=R, R^n=R^{n-1}\circ R$

$R^0 = \{<x,x> | x \in A\} = I_A$

$R^1=R$

$R^{n}=R^{n-1} \circ R$

设A为n元集， R是A上的关系，则存在自然数s和t，使得$R^s = R^t$

证：R为A上的关系，由于|A|=n, A上的不同关系只有$2^{n^{2}}$ 个。当列出R的各次幂 $R^0, R^1, R^2, ...$

必然存在自然数s和t使得$R^s = R^t$ 抽屉/鸽舍原理

R 是A上的关系， $m,n \in N$ 则

$R^{m} \circ R^n = R^{m+n}$

$(R^m)^n = R^{mn}$

布尔运算

如果矩阵中的每个元素要么是1要么是0，则称为矩阵为布尔矩阵

A与B的并

设$A=[a_{ij}], B=[b_{ij}]$ 均为$m\times n$ 的布尔矩阵，定义 $A\or B=C=[c_{ij}]$

\[c_{ij}=\begin{cases} 1 \;\;\;\; a_{ij} =1 或 b_{ij} =1 \\ 0 \;\;\;\; a_{ij} =0 且 b_{ij} =0 \\ \end{cases} \]

A与B的交

设$A=[a_{ij}], B=[b_{ij}]$ 均为$m\times n$ 的布尔矩阵，定义 $A\and B=C=[c_{ij}]$

\[c_{ij}=\begin{cases} 1 \;\;\;\; a_{ij} =1 且 b_{ij} =1 \\ 0 \;\;\;\; a_{ij} =0 或 b_{ij} =0 \\ \end{cases} \]

A与B的布尔积

设$A=[a_{ij}]$为 $m\times p$的布尔矩阵， $B=[b_{ij}]$ 为$p\times n$ 的布尔矩阵，定义 $A\bigodot B=C=[c_{ij}]$

\[c_{ij}=\begin{cases} 1 \;\;\;\; \exist_k \;,\; 1\leq k \leq n, 使得 a_{ik} =1 且 b_{kj} =1 \\ 0 \;\;\;\; 否则 \end{cases} \]

设R和S是集合A到B的二元关系，则

$M_{R\cap S} = M_R \and M_S$

$M_{R\cup S}=M_R \or M_S$

$M_{R^{-1}}=(M_R)^T$ 转置

闭包

R是集合A上的关系， $A \neq \emptyset $ R的自反、对称、传递闭包是A上的关系$R'$，使得$R'$ 满足以下条件

$R'$是自反的（对称的、传递的）

$R \subseteq R'$

对A上任何包含R的自反（对称或传递）关系 $R''$有 $R' \subseteq R''$

一般将R的自反闭包记为$r(R)$、R的对称闭包记为$s(R)$、R的传递闭包记为$t(R)$;

上面三点要求可以总结为：

自反闭包：最小的，包含R的自反关系

对称闭包：最小的，包含R的对称关系

传递闭包：最小的，包含R的对称关系

举例，自反闭包：

$A=\{1，2，3\}$

$R = \{<1,1>, <1,2>\}$

$R^{'}=\{<1,1>, <2,2>,<3,3>, <1,2>\}$

$R^{''}=\{<1,1>, <2,2>,<3,3>, <1,2>,<2,3>,<3,2>\}$

$R^{'} \subseteq R^{''}$

掌握证明

⭐⭐⭐ R为有穷集合A（|A|=n) 上的关系，则有

$r(R) = R \cup I_A$

$s(R)=R \cup R^{-1}$

$t(R)=R\cup R^2 \cup R^3\cup ... \cup R^n = \cup_{i=1}^{\infty}R^i$

设R是A上的关系，则

R在A上自反当且仅当 $I_A \subseteq R$

R在A上反自反当且仅当 $R\cap I_A = \emptyset $

R在A上对称当且仅当 $R = R^{-1}$

R在A上反对称当且仅当 $R \cap R^{-1} \subseteq I_A$

R在A上传递当且仅当 $R\circ R \subseteq R$ 或 $R^n \subseteq R$

\[\begin{align} &R 在A上自反 \\ &\Lrarr \forall_x \in A \and <x,x> \in R \\ &\Lrarr I_A \subseteq R \end{align} \]

\[\begin{align} 设R在A上反自反 , &R \cap I_A \neq \emptyset\\ &则 \exist_x \in A 使得 <x,x> \in R \cap I_A \\ &故 <x,x> \in R; 这与R在A上反自反矛盾 \\ 反之，&若 R \cap I_A = \emptyset \\ &则 \forall_x \in A \and <x,x> \notin R \\ &因此R在A上反自反 \end{align} \]

\[\begin{align} 设R在A上对称， &则 \forall <x,y> \in R 有 <y,x> \in R \\ &既 <x,y> \in R^{-1}, 故 R \subseteq R^{-1} \\ 反之， &\forall <y,x> \in R^{-1}, 则<x,y> \in R \\ &又 R 对称，故 <y,x> \in R \\ 因此， &R^{-1} \subseteq R,故 R=R^{-1} \\ 反之， &设R= R^{-1} \\ &则 \forall<x,y> \in R 有 <y,x> \in R^{-1} \\ 因此， &<y,x> \in R , 故R在A上对称 \end{align} \]

\[\begin{align} 设R在A上反对称， & 则<x,y> \in R \cap R^{-1} , 有 <x,y> \in R 且 <x,y> \in R^{-1}\\ &故 <y,x> \in R , 故 x=y, 即 <x,y> \in I_A\\ &故 R \cap R^{-1} \subseteq I_A\\ 反之， &若R \cap R^{-1} \subseteq I_A \\ &\forall <x,y> \in R , <y,x> \in R , 则 <x,y> \in R^{-1} \\ &即 <x,y> \in R \cap R……{-1}\\ &故 <x,y> \in I_A R, 因此x=y \\ &故R在A上对称 \end{align} \]

\[\begin{align} 设R在A上传递，& \forall <x,z> \in R^2, 则\exist_y 使得<x,y> \in R, <y,z> \in R \\ &又 R 在A上传递，故<x,z> \in R\\ &故R^2 \subseteq R\\ 反之， &若 R^2 \subseteq R \\ &\forall <x,y> \in R, <y,z> \in R \\ &则 <x,z> \in R^2 \\ &故 <x,z> \in R \\ &因此R在A上传递 \end{align} \]

等价关系与序关系

等价关系

相容关系

给定集合A上的关系$\rho$, 若$\rho$ 是自反的、对称的，则称$\rho$是A上的相容关系。

等价关系

R是非空集合A上的关系，若R是自反的、对称的、传递的，则称R为A上的等价关系。

设R为等价关系，若 $<x,y> \in R$ 称x等价于y，记作 $x \sim y$

设$A=\{1，2，...，10\}$, 定义A上的同余关系: $R=\{<x,y>|x \in A \and y \in A \and x \equiv y(mod 3)\}$ 证明R是等价关系

说明： R是同余关系，即若$<x,y> \in R$,则 x除以3与y除以3后得到的余数相同。

如果a，b除以m的余数相同，那么a与b的差是m的倍数

\[\begin{align} \forall_a \in A & \\ &有a \equiv a(mod 3)成立，即<a,a> \in R\\ &故R是自反的 \\ \forall<a,b> &\\ &<a,b> \in R \\ &\Lrarr a \equiv b( mod 3)\\ & \Lrarr \exist_t(t \in Z \and a-b = 3 \times t)\\ & \Lrarr b-a = -3 \times t \\ & \Lrarr <b,a> \in R\\ & 故R是对称的 \\ \forall <a,b> , <b,c> &\\ &<a,b> \in R \and <b,c> \in R \\ &\Lrarr a \equiv b(mod 3) \and b \equiv c (mod 3)\\ &\Lrarr \exist_t(t \in Z \and a-b=3\times t) \and \exist_r(r \in Z \and b-c=3 \times r)\\ &\Lrarr a-c=3\times (t+r)\\ &\Lrarr a \equiv c(mod 3)\\ &\Lrarr <a,c> \in R\\ & 故R是传递的 \\ 综上，R是等价关系 \end{align} \]

等价类

R是非空集合上A上的等价关系，称$[x]_R$为x关于R的等价类，简称为x的等价类。

在不引起歧义的情况下简记为$[x]$

上述同余关系中， $[1]=[4]=[7]=[10]$ , $[2]=[5]=[8]$, $[3]=[6]=[9]$

$[1]=\{1,4,7,10\}$, $[2]=\{2,5,8\}$, $[3]=\{3,6,9\}$

等价类[x]是由A中所有与x等价的元素构成的集合

给定非空集合A上的等价关系R

$\forall_x \in A, [x]$ 是A的非空子集

$\forall a,b \in R 有 aRb$, 当且仅当$[a]_R=[b]_R$

$\forall x,y \in A 如果没有 xRy$, 则[x]与[y]不相交

所有等价类并等于A

划分、分块

设A是非空集合， $\pi = {S_1, S_2, ...,S_m}, S_i \neq \empty, i=1,2,...,m $且满足

$\forall S_i \subseteq \pi \;\;, \;\; S_i \subseteq A$

$S_1 \cup S_2 \cup ... \cup S_m = A$

$S_i \cap S_j = \empty, i \neq j$ 任意两集合不相交

称S是A的划分，每个$S_i$ 称为一个分块

集合A上的一个划分确定A的元素之间的一个等价关系，划分中的集合是等价类。

示例：设 $X=\{1，2，3，4\}$ X的划分$S=\{\{1\}, \{2,3\}, \{4\}\}$ 写出S导出的等价关系R

R={<1,1>, <2,2>,<2,3>, <3,2>, <3,3>, <4,4>}

由等价关系写划分块

R={<1,1>, <2,2>,<2,3>, <3,2>, <3,3>, <4,4>}
S={{1，2，3}， {3}， {4}}
1，2，3 之间都存在aRb, 3和4都只和自己有关系。

序关系

偏序关系

非空集合上的自反、反对称的和传递的关系，称为A上的偏序关系，记作$\leq$;

设$\leq$为偏序关系，如果$<x,y> \in \leq$ 则记为 $x\leq y$ 读作"x 小于或等于y"

集合A和A上的偏序关系$\leq$ 一起叫做偏序集，记作 $<A, \leq>$

典型实例 A为有限集

A上的恒等关系$I_A$
小于等于关系、大于等于关系
整除关系
包含关系，即$<P(A), \subseteq>$

偏序描述的是元素之间的顺序性，当 $<x,y> \in \leq$ 时，表示的是x排在y的前面或x就是y

可比

设$\leq$是非空集合A上的偏序关系，对 $\forall a,b \in A $ 若 $<a,b> \in \leq 且 a \neq b $ , 称a小于b，记为 $a < b$;

若$<a,b> \in \leq 或 <b,a> \in \leq$ ，称a与b是可比的，否则a与b不可比

覆盖

设R为非空集合A上的偏序关系，$x,y \in A$ 如果 $x < y$ ($x\neq y$) 且不存在 $z \in A$ 使得 $x < z < y$ 则称 y覆盖x。

$COVA = \{<a,b> | a \in A \and b \in A \and b 覆盖 a\}$

集合A={1，2，3，4，5，6，12}，求集合A的整除关系的COVA

$X=\{<1,2>, <1,3>, <1,5>, <2,4>, <2,6>, <3,6>, <4,12>, <6,12>\}$

盖住元素不唯一

盖住元素可能不存在

哈斯图

利用偏序自反、反对称、传递性简化的关系图

每个节点没有环
两个联通的结点之间的序关系通过结点位置的高低表示
位置低的元素的顺序在前，具有覆盖关系的两个结点之间连边

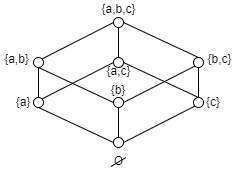
$以A=\{a,b,c\}$为例，画出偏序集$<P(A), \subseteq>$ 的哈斯图。

$P(A)=\{\empty,\{a\},\{b\},\{c\},\{a,b\},\{b,c\},\{a,c\},\{a,b,c\}\}$

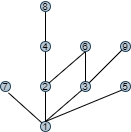
$以A=\{1,2,3,4,5,6,7,8,9\}$为例，$\leq$为整除关系，求COVA，画出偏序集的哈斯图。

\[\begin{align} \leq=\{&<1,1>,<1,2>,<1,3>,<1,4>,<1,5>,<1,6>,<1,7>,<1,8>,<1,9>, \\ &<2,4>,<2,6>,<2,8>,<2,9>,\\ &<3,3>,<3,6>,<3,9>,<4,4>,<4,8>,\\ &<5,5>,<6,6>,<7,7>,<8,8>,<9,9>\} \end{align} \]

\[COVA=\{<1,2>,<1,3>,<1,5>,<1,7>,<2,4>,<2,6>,<3,6>,<3,9>,<4,8>\} \]
<2,6>,< 3,6> 6同时覆盖2和3。 2不能整除3，所3不在2和6中间。

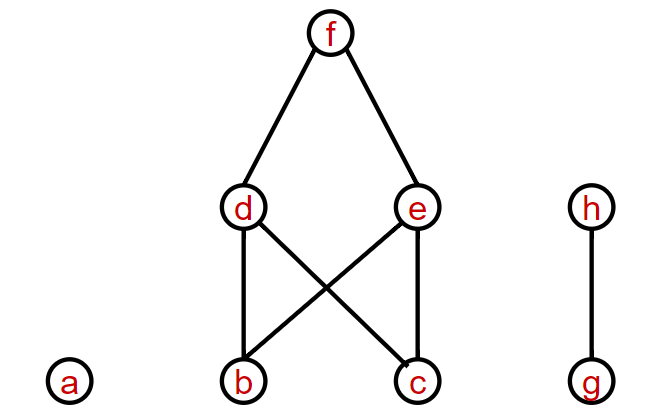
根据哈斯图求集合A和关系R的表达式

$A=\{a,b,c,d,e,f,g,h\}$

$R=\{<b,d>,<b,e>,<b,f>,<c,d>,<c,e>,<c,f>,<d,f>,<e,f>,<g,h>\} \cup I_A$

拟序关系

设集A上的二元关系R若是反自反和传递的，称R为A上的拟序关系，记为 $<A, <>$ ,称为拟序集。例如：

实数上的小于

集合A幂集上的真包含

集合A上的二元关系是拟序的，则R必然是反对称的。

全序关系

R为非空集合A上的偏序， $\forall x,y \in A $, 若必有 $x \leq y 或 y\leq x$, 即x与y都是可比的，则称R为全序(线序)。

实例：数集上的小于或等于关系是全序关系；整除关系不是正整数集合上的全序关系。

特殊元素

设$<A, \leq>$ 为偏序集， $B \subseteq A, y \in B$

若 $\forall x(x \in B\rarr y \leq x) $成立，则称y为B的最小元

若 $\forall x(x \in B\rarr x \leq y) $成立，则称y为B的最大元

若 $\neg\exist x(x \in B\and x < y) $成立，则称y为B的极小元

若 $\neg\exist x(x \in B\and y < x)$成立，则称y为B的极大元

最小元x，与集合B中所有元素都可比，且都小于等于这些元素
最大元x，与集合B中所有元素都可比，且都大于这些元素
极大元x，集合B中没有比x大的元素，x就是极大元，极大元可以有多个；极大元如果只有一个，则它就是最大元
极小元x，集合B中没有比x小的元素，x就是极小元，极小元可以有多个；极小元如果只有一个，则它就是最小元

设$<A, \leq>$ 为偏序集， $B \subseteq A, y \in A$

若 $\forall x(x \in B\rarr x \leq y) $成立，则称y为B的上界

若 $\forall x(x \in B\rarr y \leq x) $成立，则称y为B的下界

令 $C=\{y|y是B的上界\}$，称C的最小元为B的最小上界（上确界）

令 $C=\{y|y是B的上界\}$，称C的最大元为B的最大下界（下确界）

函数

设F为二元关系，若 $\forall x \in domF$ 都存在唯一的 $y \in ran F$ 使 xFy成立，则称F为函数。

对于函数F，如果有$xFy$，则记作 $y=F(x)$, 并称y为F在x的值。

设F、G为函数，则 $F=G \Lrarr F \subseteq G \and G \subseteq F$

如果两个函数相等，一定满足如下两个条件：

$domF = domG$

$\forall_x \in domF = dom G 都有 F(x)=G(x)$

函数 $F(x)=(x^2-1)/(x+1) G(x)=x-1 不相等，因为 domF\subset domG$.

设A、B为集合，如果f为函数， $dom f = A, ran f \subseteq B$, 则称f为从A到B的函数，记作 $f:A\rarr B$.

函数的定义域等于A，值域是B的子集

$f:N\rarr N, f(x)=2x$ 是从N到N的函数

$f:N\rarr N, g(x)=2$ 是从N到N的函数

所有从A到B的函数的集合记作 $B^A$, 读作：B上A，符号化表示为$B^A=\{f|f:A \rarr B\}$

计数：$|A|=m, |B|=n, m,n>0, |B^A|=n^m$

$A=\empty 则 B^A=B^{\empty}=\{\empty\}$

$A\neq \empty 且B=\empty 则 B^A=\empty^A=\empty$

像

设函数$f:A\rarr B, A_1\subseteq A$

A_1在f下的下给你： $f(A_1)=\{f(x)| x\in A_1\}$, 函数的像 $f(A)$

注意：函数值 $f(x) \in B$, 而像$f(A_1) \subseteq B$

\[设 f:N\rarr N 且 f(x)= \begin{cases} x /2 \;\;\;\; &\text{若x为偶数}\\ x +1 \;\;\;\; &\text{若x为奇数} \end{cases}\\ 令A={0,1},B={2}, 那么有\\ f(A)=f(\{0,1\})=\{f(0),f(1)\}=\{0,2\} \]

值域就是像？

满射、单射、双射

设 $f:A\rarr B$

若$ran f=B$, 则称$f:A \rarr B$ 是满射的

若 $\forall y\in ran f$ 都是唯一的 $x\in A￥使得 $f(x)=y$, 则称$f:A\rarr B $是单射（入设）

若 $f: A \rarr B$ 既是满射又是单射的，则称 $f:A \rarr B $是双射的

f满射意味着： $\forall_y \in B$ 都存在 $x\in A$ 使得$f(x)=y$

f单射意味着： $f(x_1)=f(x_2) \Rarr x_1=x_2$

函数的复合

设F、G是函数，则$F \circ G$ 也是函数，且满足：

$dom (F \circ G)={x | x\in domF \and F(x) \in dom G}$

$\forall_x \in dom(F \circ G) 有 F \circ G(x) =G(F(x))$

计算题

\[设f:R \rarr R, G:R \rarr R\\ f(x)= \begin{cases} x^2 & x \geq 3\\ -2 & x <3 \end{cases} \;\;\;\;\;\;\;\;\;\;\;\;\; g(x)=x + 2 \]

求$f\circ g, g \circ f$
如果f和g存在反函数，求出它们的反函数

\[\begin{align} f\circ g=f\circ g(x)=g(f(x)) =f(x)+2=\begin{cases} x^2+2 & x\geq 3 \\ 0 &x <3 \end{cases} \\ -------------------------\\ g \circ f= f(g(x))=f(x+2)=\begin{cases} (x+2)^2 & x \geq 1 \\ -2 & x<1 \end{cases} \end{align} \]

posted @ 2023-07-02 23:28 Dreamsrj 阅读(189) 评论(0) 收藏举报

刷新页面返回顶部

Dreamsrj