面试算法学习1
蛇形矩阵
微软面试题
题目描述
输入两个整数 \(n\) 和 \(m\),输出一个 \(n\) 行 \(m\) 列的矩阵,将数字 \(1\) 到 \(n \times m\) 按照回字蛇形填充至矩阵中。
具体矩阵形式可参考样例。
输入格式
输入共一行,包含两个整数 \(n\) 和 \(m\)。
输出格式
输出满足要求的矩阵。
矩阵占 \(n\) 行,每行包含 \(m\) 个空格隔开的整数。
数据范围
\(1 \le n,m \le 100\)
解法
模拟法:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110;
int n,m,a[N][N];
int main(){
cin>>n>>m;
int l = 0,r = m-1, t = 0,d = n-1,cnt=1;
while(l<=r || t <= d){
for(int i=l;i<=r && t<=d;i++) a[t][i] = cnt++;t++;
for(int i=t;i<=d && l<=r;i++) a[i][r] = cnt++;r--;
for(int i=r;i>=l && t<=d;i--) a[d][i] = cnt++;d--;
for(int i=d;i>=t && l<=r;i--) a[i][l] = cnt++;l++;
}
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
cout<<a[i][j]<<" \n"[j==m-1];
return 0;
}
触底模拟:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110;
int n,m,a[N][N],dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};
int main(){
cin>>n>>m;int x=0,y=0;
for(int i=1,u=0;i<=n*m;i++){
a[x][y] = i;
x += dx[u];y += dy[u];
if(a[x][y] || x<0 || y<0 || x>=n || y>=m)
x-=dx[u],y-=dy[u],u = (u+1)%4,
x += dx[u],y += dy[u];
}
for(int i=0;i<n;i++) for(int j=0;j<m;j++)
cout<<a[i][j]<<" \n"[j==m-1];
return 0;
}
单链表快速排序
旷视面试题
题目描述
给定一个单链表,请使用快速排序算法对其排序。
要求:期望平均时间复杂度为 \(O(nlogn)\),期望额外空间复杂度为 \(O(logn)\)。
思考题: 如果只能改变链表结构,不能修改每个节点的val值该如何做呢?
数据范围
链表中的所有数大小均在 \(int\) 范围内,链表长度在 \([0, 10000]\)。
本题数据完全随机生成。
解法
思路与普通的快排基本一致,将链表根据一个val分成小于val、等于val、大于val三段,再对前后两段递归进行快排,对于排序完的三段从前到后进行拼接即可完成。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* quickSortList(ListNode* head) {
if(!head || !head->next) return head;
auto left = new ListNode(-1),mid=new ListNode(-1),right=new ListNode(-1),
ltail = left,mtail = mid,rtail = right;
int val = head->val;
for(auto p=head;p;p = p->next){
if(p->val < val) ltail = ltail->next = p;
else if(p->val == val) mtail = mtail->next = p;
else rtail = rtail->next = p;
}
ltail->next = mtail->next = rtail->next = NULL;
left->next = quickSortList(left->next);
right->next = quickSortList(right->next);
get_tail(left)->next = mid->next;
get_tail(left)->next = right->next;
auto p = left->next;
delete left;delete mid;delete right;
return p;
}
ListNode* get_tail(ListNode* head) {
while (head->next) head = head->next;
return head;
}
};
寻找峰值
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
提示:
1 <= nums.length <= 1000-231 <= nums[i] <= 231 - 1- 对于所有有效的
i都有nums[i] != nums[i + 1]
解法
可以发现当存在斜坡时,顺着高点的方向就可以找到答案。
class Solution {
public:
int findPeakElement(vector<int>& nums) {
int l=0,r = nums.size()-1;
while(l<r){
int mid = (l+r) >> 1;
long long lm = mid-1,rm = mid+1;
if(lm<0) lm = INT_MIN-1ll;
else lm = nums[lm];
if(rm>=nums.size()) rm = INT_MIN-1ll;
else rm = nums[rm];
long long key = nums[mid];
if(key>lm && key>rm)
return mid;
else if(key>lm &&rm>key)
l = mid+1;
else
r = mid-1;
}return l;
}
};
寻找矩阵的极小值
微软面试题
题目描述
给定一个 \(n \times n\) 的矩阵,矩阵中包含 \(n \times n\) 个 互不相同 的整数。
定义极小值:如果一个数的值比与它相邻的所有数字的值都小,则这个数值就被称为极小值。
一个数的相邻数字是指其上下左右四个方向相邻的四个数字,另外注意,处于边界或角落的数的相邻数字可能少于四个。
要求在 \(O(nlogn)\) 的时间复杂度之内找出任意一个极小值的位置,并输出它在第几行第几列。
本题中矩阵是隐藏的,你可以通过我们预设的 \(int\) 函数 \(query\) 来获得矩阵中某个位置的数值是多少。
例如,\(query(a,b)\) 即可获得矩阵中第 \(a\) 行第 \(b\) 列的位置的数值。
注意:
- 矩阵的行和列均从 \(0\) 开始编号。
query()函数的调用次数不能超过 \((n + 2) \times \lceil log_2n \rceil + n\)。- 答案不唯一,输出任意一个极小值的位置即可。
数据范围
\(1 \le n \le 300\),矩阵中的整数在int范围内。
解法
与上题类似,同时通过调用次数可以获取提示:我们可以对\(log_2n\)列遍历其中的n个数。具体做法是:
通过二分确定包含极小值的列,对该列进行遍历即可得到答案,其中二分的条件是一列的最小值与其所在行左右值的大小比较。
// Forward declaration of queryAPI.
// int query(int x, int y);
// return int means matrix[x][y].
class Solution {
public:
vector<int> getMinimumValue(int n) {
typedef long long ll;
ll INF = 1e15;
int l,r;l=0;r = n-1;
while(l<r){
int mid = l+r>>1;
ll val = INF;
int p=0;
for(int i=0;i<n;i++){
int t = query(i,mid);
if(t < val)
val = t,p = i;
}
ll lt = mid ? query(p,mid-1):INF;
ll rt = mid+1<n ? query(p,mid+1):INF;
if(val<lt && val<rt)
return {p,mid};
if(lt<val)
r = mid - 1;
else
l = mid + 1;
}
ll val = INF;int p=0;
for(int i=0;i<n;i++){
int t = query(i,r);
if(t<val)
val = t,p = i;
}
return {p,r};
}
};
鸡蛋的硬度
google面试题
输入格式
输入包括多组数据,每组数据一行,包含两个正整数 \(n\) 和 \(m\),其中 \(n\) 表示楼的高度,\(m\) 表示你现在拥有的鸡蛋个数,这些鸡蛋硬度相同(即它们从同样高的地方掉下来要么都摔碎要么都不碎),并且小于等于 \(n\)。
你可以假定硬度为 \(x\) 的鸡蛋从高度小于等于 \(x\) 的地方摔无论如何都不会碎(没摔碎的鸡蛋可以继续使用),而只要从比 \(x\) 高的地方扔必然会碎。
对每组输入数据,你可以假定鸡蛋的硬度在 \(0\) 至 \(n\) 之间,即在 \(n+1\) 层扔鸡蛋一定会碎。
输出格式
对于每一组输入,输出一个整数,表示使用最优策略在最坏情况下所需要的扔鸡蛋次数。
数据范围
\(1 \le n \le 100\),
\(1 \le m \le 10\)
样例解释
最优策略指在最坏情况下所需要的扔鸡蛋次数最少的策略。
如果只有一个鸡蛋,你只能从第一层开始扔,在最坏的情况下,鸡蛋的硬度是100,所以需要扔100次。如果采用其他策略,你可能无法测出鸡蛋的硬度(比如你第一次在第二层的地方扔,结果碎了,这时你不能确定硬度是0还是1),即在最坏情况下你需要扔无限次,所以第一组数据的答案是100。
解法
dp1
用f[i][j]来表示在区间长度为i中通过j个鸡蛋得到的最优策略。
对于每个鸡蛋j,可以考虑有两种情况:没用鸡蛋j,即f[i][j]=f[i][j-1];使用了鸡蛋j,对于其1~i间有i种情况,令其中一种情况为k,此时会有两种情况:鸡蛋碎了(f[k-1][j-1]),鸡蛋没碎(f[i-k][j]),最坏情况即为两者取最大值,此时的最少策略为min(f[i][j],max(f[k-1][j-1],f[i-k][j])+1)
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N =110,M=11;
int n,m,f[N][M];
int main(){
while(cin>>n>>m){
for(int i=1;i<=n;i++) f[i][1] = i;
for(int i=1;i<=m;i++) f[1][i] = 1;
for(int i=2;i<=n;i++)
for(int j=2;j<=m;j++){
f[i][j] = f[i][j-1];
for(int k=1;k<=i;k++)
f[i][j] = min(f[i][j],max(f[k-1][j-1],f[i-k][j])+1);
}
cout<<f[n][m]<<endl;
}return 0;
}
dp2
与上一种方法不同,用f[i][j]来表示的是用在i次测量中用j个鸡蛋能测得的最大长度。
假设测量位置k,会有两种情况:鸡蛋碎了(f[i-1][j-1],递归下半部分)或者不碎(f[i-1][j],递归上半部分)。
f[i][j] = f[i-1][j]+f[i-1][j-1]+1;
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N =110,M=11;
int n,m,f[N][M];
int main(){
while(cin>>n>>m){
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)
f[i][j] = f[i-1][j]+f[i-1][j-1]+1;
if(f[i][m] >= n){
cout<<i<<endl;
break;
}
}
}return 0;
}
包含min函数的栈
hulu面试题
题目描述
设计一个支持push,pop,top等操作并且可以在O(1)时间内检索出最小元素的堆栈。
- push(x)–将元素x插入栈中
- pop()–移除栈顶元素
- top()–得到栈顶元素
- getMin()–得到栈中最小元素
数据范围
操作命令总数 \([0,100]\)。
样例
MStack minStack = new MStack();
minStack.push(-1);
minStack.push(3);
minStack.push(-4);
minStack.getM(); --> Returns -4.
minStack.pop();
minStack.top(); --> Returns 3.
minStack.getM(); --> Returns -1.
解法
方法一
直接通过一个数组来存存入数时当前位的最小值即可。
class MinStack {
public:
/** initialize your data structure here. */
int len;
int a[110],ck[110];
MinStack() {
len = a[0] = ck[0] = 0;
}
void push(int x) {
a[len] = x;
ck[len] = min(len?ck[len-1]:x,x);
len++;
}
void pop() {
len--;
}
int top() {
return a[len-1];
}
int getMin() {
return ck[len-1];
}
};
方法二
通过一个单调栈来维护最小值。
通过ck.top() >= x来使存在ck中的为单调递减的最小值。当进行pop时,只要不与ck当前的最小值相等就不需要对ck进行更新。获取最小值时获取ck.top()即可。
class MinStack {
public:
/** initialize your data structure here. */
stack<int> a;
stack<int> ck;
MinStack() {
}
void push(int x) {
a.push(x);
if(ck.empty() || ck.top() >= x)
ck.push(x);
}
void pop() {
if(ck.top() == a.top())
ck.pop();
a.pop();
}
int top() {
return a.top();
}
int getMin() {
return ck.top();
}
};
链表中环的入口结点
阿里面试题
题目描述
给定一个链表,若其中包含环,则输出环的入口节点。
若其中不包含环,则输出null。
数据范围
节点 val 值取值范围 \([1,1000]\)。
节点 val 值各不相同。
链表长度 \([0,500]\)。
样例
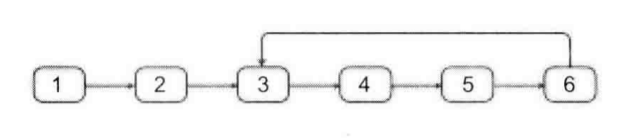
给定如上所示的链表:
[1, 2, 3, 4, 5, 6]
2
注意,这里的2表示编号是2的节点,节点编号从0开始。所以编号是2的节点就是val等于3的节点。
则输出环的入口节点3.
解法
可以发现val值不同且范围只有1000,使用用个数组记录下用过的val值对应的节点就行了。当再访问到记录过的val时,就是发生了循环。
class Solution {
public:
ListNode *entryNodeOfLoop(ListNode *head) {
ListNode* ck[1010];
for(auto p=head;p;p=p->next){
int val = p->val;
if(ck[val])
return ck[val];
ck[val] = p;
}return NULL;
}
};



 浙公网安备 33010602011771号
浙公网安备 33010602011771号