最大似然估计,散度,交叉熵
如果这个信息,可以将之前非常不确定的事情,确定了,说明这个信息的信息量很大!
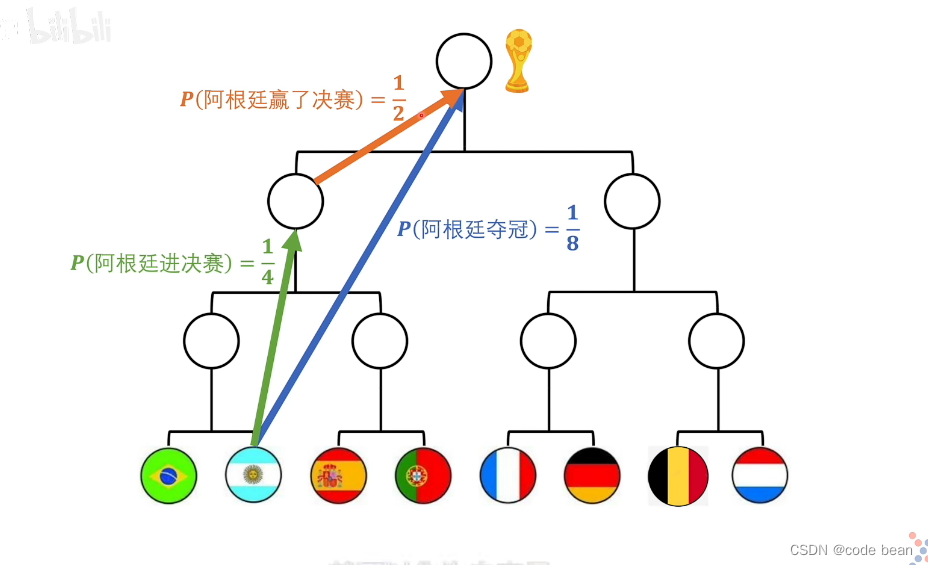
这张图是解释,数学家如何定义信息量的过程:

也就是说,阿根廷夺冠的信息量 = 阿根廷进决赛的信息量+阿根廷赢了决赛的信息量,但是x本身是概率,所以这里的1/8 是 x1*x2 的结果。及:
![]()
这种特性是log特有的。 然后底数大于1的时候,log单调递增,所以加上负号让其单独递减。
到此信息量的定义完成了。
接下看信息熵的定义:
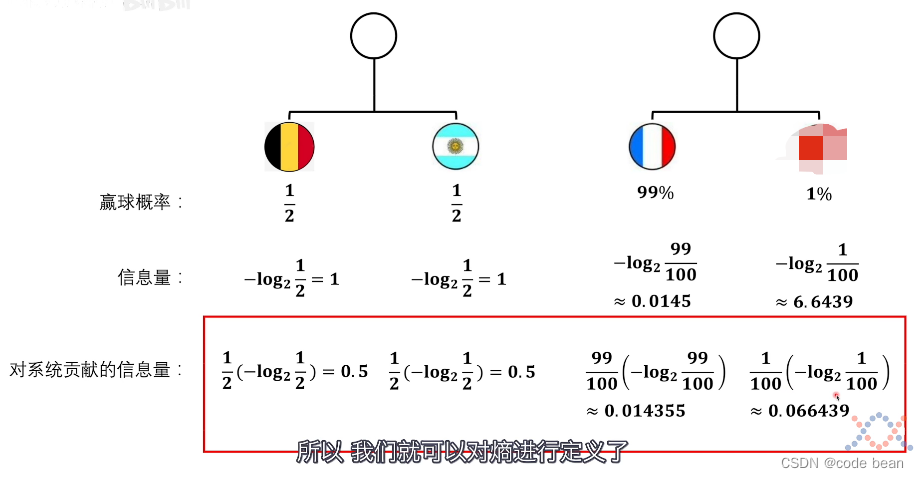
求信息熵的过程就是求期望的过程:信息量乘以事件发生的概率,然后求和。
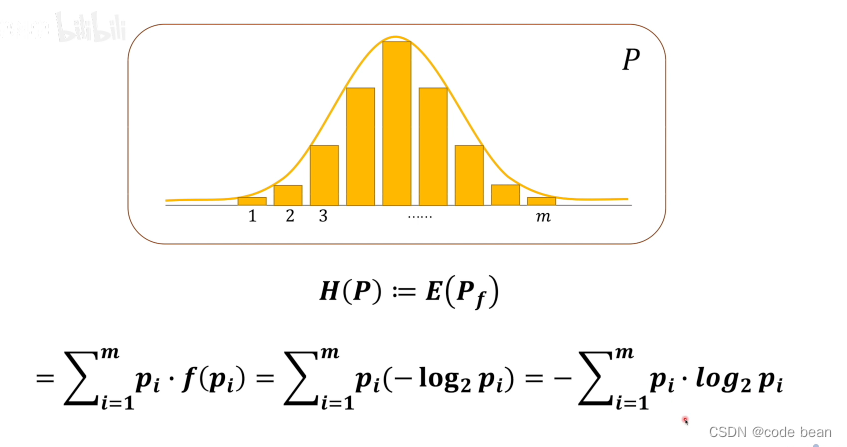
信息熵,描述的是“消息”的不确定性程度或者说是混乱程度。而这里的“消息”是可以看成一个概率模型的。而求概率模型的信息熵,就是求概率模型的期望啊!
如果想对比两个模型的分布差异,就需要一个概念叫做相对熵(KL散度)
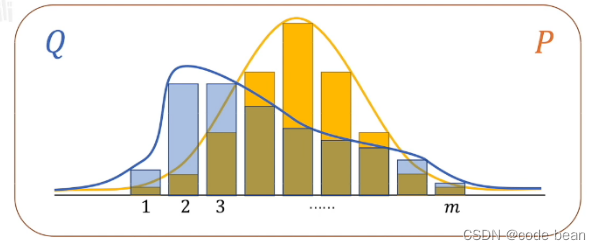
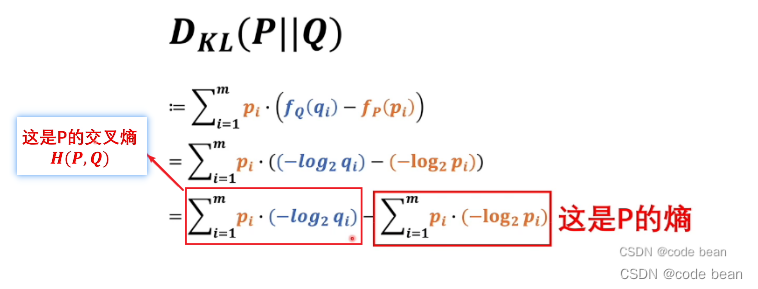
这里有个证明,交叉熵一定大于熵:

所以如果要两个模型最接近,那就是求交叉熵的最小值。那深度学习干的事情就是让神经网络这个模型逼近人脑模型。所以神经网络和人脑模型的交叉熵,就可以作为损失函数!(交叉熵越小,两个模型越相近)
那如下函数,其实是,一个二分类的交叉熵的展开:
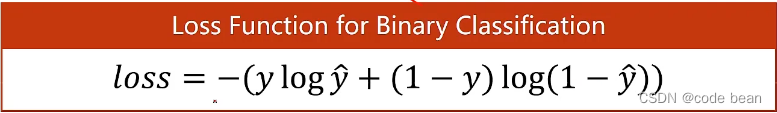
这里Y是人的判定,只有两种可能,1或者0,而yhead,是神经网络的输出值,是个概率。他们之间形成的交叉熵构成了二分类的损失函数。

参考:
作者:宋桓公
出处:http://www.cnblogs.com/douzi2/
如果您觉得阅读本文对您有帮助,请点一下“推荐”按钮,您的“推荐”将是我最大的写作动力!欢迎各位转载,但是未经作者本人同意,转载文章之后必须在文章页面明显位置给出作者和原文连接,否则保留追究法律责任的权利。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号