二叉树

 

 

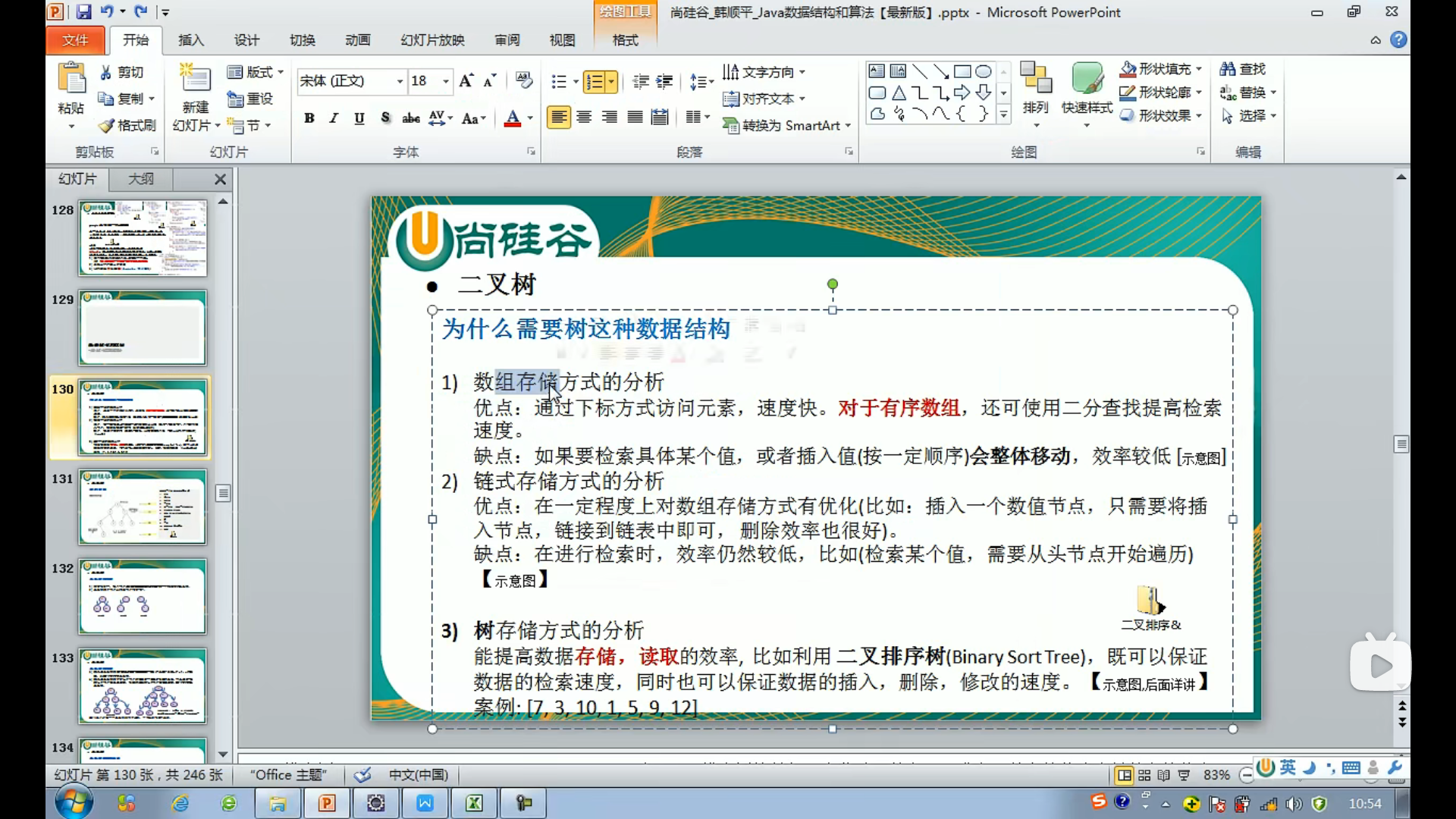
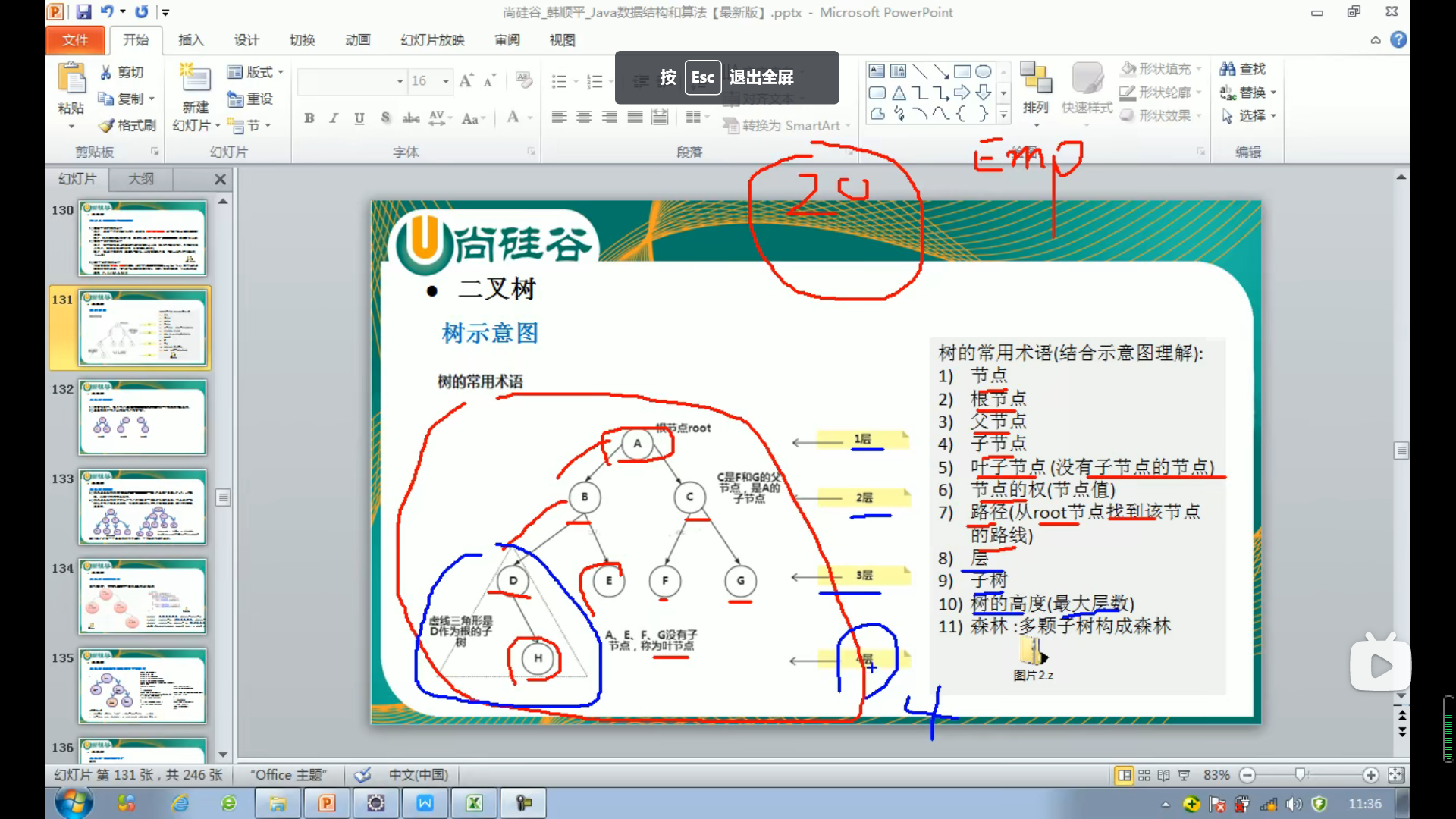
前，中，后序遍历：

前：父节点->左子树->右子树

中：左->父->右

后：左->右->父

 

public class erchashu {
    public static void main(String[] args) {
        Binarytree tree=new Binarytree();
        node1 root=new node1(1,"宋江");
        node1 n2=new node1(2,"吴用");
       node1 n3=new node1(3,"卢俊义");
        node1 n4=new node1(4,"林冲");
        node1 n5=new node1(5,"f");
        
        //构建二叉树，设置左右树
        root.setLeft(n2);
        root.setRight(n3);
        n3.setRight(n4);
        n3.setLeft(n5);
        tree.setRoot(root);
        
        //中序遍历二叉树
        tree.infixOrder1();

        System.out.println("search");
        //前序搜索二叉树
        node1 resnode=tree.presearch1(2);
        if(resnode!=null){
            System.out.println(resnode.getName());
        }
    }



}
//树
class Binarytree{
    //根节点，是下面node1定义的节点，所以可以调用node1中的方法
    private node1 root;

    public node1 getRoot() {
        return root;
    }

    public void setRoot(node1 root) {
        this.root = root;
    }
    //调用node1的方法
    public void preOrder1(){
        if(this.root!=null){
            this.root.preOrder();
        }else{
            System.out.println("null");
        }
    }
    public void infixOrder1(){
        if(this.root!=null){
            this.root.infixOrder();
        }else{
            System.out.println("null");
        }
    }
    public void postOrder1(){
        if(this.root!=null){
            this.root.postOrder();
        }else{
            System.out.println("null");
        }
    }

    //查找
    //调用node1里面的查找方法
    public node1 presearch1(int no){
        if(root!=null){
            return root.presearch(no);
        }
        else{
            return null;
        }
    }



}

class node1{
    int no;
    String name;
    node1 left;
    node1 right;
    public node1(int no,String name){

        this.no=no;
        this.name=name;
    }

    @Override
    public String toString() {
        return "node1{" +
                "no=" + no +
                ", name='" + name + '\'' +
                ", left=" + left +
                ", right=" + right +
                '}';
    }
    //前序遍历
//先打印出当前父节点，再打印左子树，用递归把左子树全部打印出来。再打印右子树
    public void preOrder(){
        System.out.println(this);
        if(this.left!=null){
            this.left.preOrder();
        }
        if(this.right!=null){
            this.right.preOrder();
        }
    }

    //中序遍历
    public void infixOrder(){

        if(this.left!=null){
            this.left.infixOrder();
        }
        System.out.println(this);
        if(this.right!=null){
            this.right.infixOrder();
        }
    }
    //后序遍历
    public void postOrder(){

        if(this.left!=null){
            this.left.postOrder();
        }

        if(this.right!=null){
            this.right.postOrder();
        }
        System.out.println(this);
    }
    //查找目标节点，用前序遍历。
    //先判断当前父节点是不是就是要找到数
    
    public node1 presearch(int no){
        node1 res=null;
        if(this.no==no){
            return this;
        }
        if(this.left!=null){//再判断左子树。如果左子节点不是空，就递归遍历左子树，找目标树
            res=this.left.presearch(no);
        }
        if(res!=null){
            return res;
        }
        if(this.right!=null){
            res=this.right.presearch(no);
        }
        return res;

    }
    public node1 infixsearch(int no){

        node1 res=null;
        if(this.left!=null){
            res=this.left.infixsearch(no);
        }
        if(res!=null){
            return res;
        }

        if(this.no==no){
            return this;
        }
        if(this.right!=null){
            res=this.right.infixsearch(no);
        }
        return res;
    }

    public int getNo() {
        return no;
    }

    public void setNo(int no) {
        this.no = no;
    }

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

    public node1 getLeft() {
        return left;
    }

    public void setLeft(node1 left) {
        this.left = left;
    }

    public node1 getRight() {
        return right;
    }

    public void setRight(node1 right) {
        this.right = right;
    }
}
删除节点

 

 

 

 顺序存储：

通常只考虑完全二叉树。

第n个元素左子节点为2n+1. 

右子节点为2n+2,

父节点为：(n-1)/2   

n表示二叉树中的第几个元素，从0开始算的（下标）

前序遍历：

public class try4 {


    public static void main(String[] args) {
        int[] a={1,2,3,4,5,6,7};
        try4 t=new try4(a);
        t.preorder();

    }
    private int[] arr;
    public void preorder(){
        this.preorder(0);
    }

    public try4(int[] arr) {
        this.arr = arr;
    }

    public void preorder(int index){
        if(arr==null||arr.length==0){
           System.out.println("null");
        }
        System.out.println(arr[index]);
        if((2*index+1)<arr.length){
            preorder(2*index+1);
        }
        if((2*index+2)<arr.length){
             preorder(2*index+2);
        }


    }

}