统计学习方法 学习笔记(三):支持向量机(上)
了解过感知机后,知道了感知机的固有缺点,那么在接下来的这三篇笔记中,将很好地解决感知机的约束。在这一篇笔记中,我将要介绍线性可分支持向量机,来解决感知机对于线性可分数据集会存在多个解的问题。
支持向量机:
支持向量机(support vector machines, SVM)是一种二类分类模型。它的基本模型是定义在特征空间上的间隔最大化的线性分类器,间隔最大化使它有别于感知机;支持向量机还包括核技巧,这使它成为了实质上的非线性分类器。支持向量机的学习策略就是间隔最大化,可形式化为一个求解凸二次规划的问题,也等价于正则化的hingle损失函数的最小化问题。支持向量机的学习算法是求解凸二次规划的最优化算法。
支持向量机学习方法可分为:线性可分支持向量机、线性支持向量机和非线性支持向量机。我通过三篇笔记(支持向量机(上)、支持向量机(中)及支持向量机(下))来分别介绍。
(1)当训练数据线性可分时,通过硬间隔最大化,学习一个线性的分类器,即线性可分支持向量机,又称为硬间隔支持向量机;
(2)当训练数据近似线性可分时,通过软间隔最大化,也学习一个线性的分类器,即线性支持向量机,又称为软间隔支持向量机;
(3)当训练数据线性不可分时,通过使用核技巧及软间隔最大化,学习非线性支持向量机。
线性可分支持向量机:
一般地,当训练数据集线性可分时,存在无穷个分离超平面可将两类数据正确分开。感知机利用误分类最小的策略,求得分离超平面,不过这时的解有无穷多个。线性可分支持向量机利用间隔最大化求最优分离超平面,这时,解是唯一的。
定义(线性可分支持向量机):给定线性可分训练数据集,通过间隔最大化或等价地求解相应的凸二次规划问题学习得到的分离超平面为:
$$w^*\cdot x + b^* = 0 $$
以及相应的分类决策函数:
$$f(x) = sign(w^*\cdot x + b^*)$$
称为线性可分支持向量机。
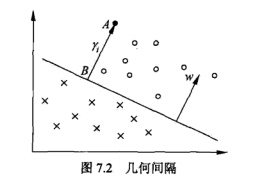
几何间隔:
如图,那个直线对应为将两类数据正确划分并且间隔最大的直线,该直线为:$w\cdot x + b = 0$,B点在直线上,A点到B点的距离,称之为几何间隔。根据上一篇感知机的介绍,知道了对于点$(x_i,y_i)$的几何间隔(到超平面,在上图指直线)为:
$$\gamma_i = y_i(\frac{w}{||w||}\cdot x_i + \frac{b}{||w||})$$
要和感知机区别的是,点$(x_i,y_i)$是被正确分类的点。定义超平面$(w,b)$关于训练数据集$T$的几何间隔为超平面$(w,b)$关于$T$中所有样本点$(x_i,y_i)$的几何间隔之最小值,即:
$$\gamma = \min_{i=1,...,N}\gamma_i$$
支持向量机学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。对于数据集$T$寻找一个超平面$(w,b)$使该数据集上的几何间隔最大化:
$$\max_{w,b} \gamma$$
$$s.t. y_i(\frac{w}{||w||}\cdot x_i + \frac{b}{||w||}) \geq \gamma, i = 1,2,3,...,N$$
约束条件表示的是超平面$(w,b)$关于每个训练样本点的几何间隔至少是$\gamma$。现在,我们要求的是参数$(w,b)$,而现在的优化目标是$\gamma$,应该再探寻一步,看看什么关于带有参数的东西是和$\gamma$是等价的。
函数间隔:
从几何间隔的定义可以知道,$ y_i(\frac{w}{||w||}\cdot x_i + \frac{b}{||w||})$表示一个点距离分离超平面的远近的绝对距离;那一个点距离分离超平面的远近的相对距离,用$y_i(w\cdot x_i + b)$表示,即在超平面$w\cdot x + b = 0$确定的情况下,在同一个数据集$T$中的各个样本到分离超平面的相对距离大小比较,不用考虑$\frac{1}{||w||}$了,和感知机损失函数的得来类似(感知机是基于误分类,这个是正确分类)。所以,这个相对距离,称之为函数间隔。
对于给定的训练数据集$T$和超平面$(w,b)$,定义超平面$(w,b)$关于样本点$(x_i,y_i)$的函数间隔为:
$$\hat{\gamma_i} = y_i(w\cdot x_i + b)$$
定义超平面$(w,b)$关于训练数据集$T$的函数间隔为超平面$(w,b)$关于$T$中所有样本点$(x_i,y_i)$的函数间隔之最小值,即:
$$\hat{\gamma} = \min_{i=1,...,N}\hat{\gamma_i}$$
所以,几何间隔和函数间隔的关系是绝对距离和相对距离,即 绝对距离=$\frac{1}{||w||} \cdot$相对距离,所以:
$$\gamma_i = \frac{\hat{\gamma_i}}{||w||}$$
$$\gamma = \frac{\hat{\gamma}}{||w||}$$
间隔最大化:
知道了几何间隔和函数间隔的关系后,可以将上述的几何间隔最大化表示为:
$$\max_{w,b} \frac{\hat{\gamma}}{||w||}$$
$$s.t. y_i(w\cdot x_i + b) \geq \hat{\gamma}, i=1,2,...,N$$
函数间隔$\hat{\gamma}$的取值并不影响最优化问题的解。事实上,假设将$w$和$b$按比例改变为$\lambda w$和$\lambda b$,这时函数间隔成为了$\lambda \hat{\gamma}$。函数间隔的这一改变对上面最优化问题的不等式约束没有影响,对目标函数的优化也没有影响,也就是说,它产生一个等价的最优化问题。这样,就可以取$\hat{\gamma} = 1$。将$\hat{\gamma} = 1$代入上面的最优化问题,注意到最大化$\frac{1}{||w||}$和最小化$\frac{1}{2}||w||^2$是等价的,于是就得到下面的线性可分支持向量机学习的最优化问题:
$$\min_{w,b} \frac{1}{2}||w||^2$$
$$s.t. y_i(w\cdot x_i + b) - 1 \geq 0, i=1,2,...,N$$
线性可分支持向量机学习算法——最大间隔法:
输入:线性可分训练数据集$T={(x_1,y_1),(x_2,y_2),...,(x_N,y_N)}$,其中,$x_i \in \mathcal{X}=R^n, y_i \in \mathcal{Y}={-1,+1},i=1,2,...,N$;
输出:最大间隔分离超平面和分类决策函数。
(1):构造并求解约束最优化问题:
$$\min_{w,b} \frac{1}{2}||w||^2$$
$$s.t. y_i(w\cdot x_i + b) - 1 \geq 0, i=1,2,...,N$$
求得最优解$w^*,b^*$。
(2):由此得到分离超平面:
$$w^*\cdot x + b^* = 0 $$
分类决策函数:
$$f(x) = sign(w^*\cdot x + b^*)$$
支持向量和间隔边界:
在线性可分情况下,训练数据集的样本点中与分离超平面距离最近的样本点的实例称为支持向量(support vector)。支持向量是使约束条件等号成立的点,即:
$$y_i(w\cdot x_i + b) - 1 = 0$$
对$y_i = +1$的正例点,支持向量在超平面
$$H_1: w\cdot x + b = 1$$
上,对$y_i = -1$的负例点,支持向量在超平面
$$H_2: w\cdot x + b = -1$$
上。如下图所示,在$H_1$和$H_2$上的点就是支持向量:
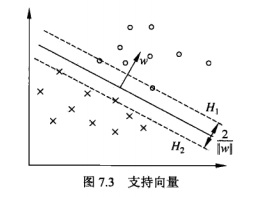
学习的对偶算法:
为了求解线性可分支持向量机的最优化问题:
$$\min_{w,b} = \frac{1}{2}||w||^2$$
$$s.t. 1 - y_i(w\cdot x_i + b) leq 0, i = 1,2,...,N$$
将它作为原始最优化问题,应用拉格朗日对偶性,通过求解对偶问题(dual problem)得到原始问题(primal problem)的最优解,这就是线性可分支持向量机的对偶算法。这样做的优点:(1)对偶问题往往更容易求解;(2)自然引入核函数,进而推广到非线性分类问题。
首先构建拉格朗日函数(Lagrange function)。为此,对每一个不等式约束可引进拉格朗日乘子(Lagrange multipiler)$\alpha_i \geq 0, i=1,2,...,N$。定义拉格朗日函数:
$$L(w,b,\alpha) = \frac{1}{2}||w||^2 - \sum_{i=1}^{N}\alpha_iy_i(w\cdot x_i + b) + \sum_{i=1}^{N}\alpha_i$$
其中,$\alpha = (\alpha_1,\alpha_2,...,\alpha_N)^T$为拉格朗日乘子 向量。
根据拉格朗日对偶性(参考拉格朗日对偶性),原始问题的对偶问题是极大极小问题:
$$\max_{\alpha}\min_{w,b} L(w,b,\alpha)$$
所以,为了得到对偶问题的解,需要先求$L(w,b,\alpha)$对$w,b$的极小,再求对$\alpha$的极大。
(1)求$\min_{w,b} L(w,b,\alpha)$
将拉格朗日函数$L(w,b,\alpha)$分别对$w,b$求偏导数并令其等于0。
$$\bigtriangledown _w L(w,b,\alpha) = w - \sum_{i=1}^{N}\alpha_iy_ix_i = 0 $$
$$\bigtriangledown_b L(w,b,\alpha) = - \sum_{i=1}^{N}\alpha_iy_i = 0 $$
得:
$$w = \sum_{i=1}^{N}\alpha_iy_ix_i$$
$$\sum_{i=1}^{N}\alpha_iy_i = 0$$
将这两个式子代入拉格朗日函数,即得:
$$L(w,b,\alpha) = \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j) - \sum_{i=1}^{N}\alpha_iy_i((\sum_{j=1}^{N}\alpha_jy_jx_j)\cdot x_i + b) + \sum_{i=1}^{N}\alpha_i\\=-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j) + \sum_{i=1}^{N}\alpha_i$$
即:
$$\min_{w,b} L(w,b,\alpha)= -\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j) + \sum_{i=1}^{N}\alpha_i$$
(2)求$\min_{w,b} L(w,b,\alpha)$对$\alpha$的极大,即是对偶问题
$$\max_{\alpha} -\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j) + \sum{i=1}^{N}\alpha_i$$
$$ s.t. \sum_{i=1}^{N}\alpha_iy_i = 0$$
$$ \alpha_i \geq 0, i=1,2,...,N$$
将目标函数由求极大转换成求极小,就得到了下面与之等价的对偶最优化问题:
$$\min_{\alpha} \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j) - \sum{i=1}^{N}\alpha_i$$
$$ s.t. \sum_{i=1}^{N}\alpha_iy_i = 0$$
$$ \alpha_i \geq 0, i=1,2,...,N$$
设$\alpha^* = (\alpha_{1}^{*},\alpha_{2}^{*},...,\alpha_{N}^{*})^T$是对偶最优化问题的解,则存在下标$j$,使得$a_{j}^{*} > 0$,并可按下式求得原始最优化问题的解:$w^{*},b^{*}$:
$$w^{*} = \sum_{i=1}^{N}\alpha_{i}^{*}y_ix_i$$
$$b^* = y_j - \sum_{i=1}^{N}\alpha_{i}^{*}y_i(x_i\cdot x_j)$$
$w^{*},b^{*}$和$\alpha^*$分别是原始问题和对偶问题的解的充分必要条件是$w^{*},b^{*}$和$\alpha^*$满足下面的$KKT$条件:
$$\bigtriangledown _w L(w,b,\alpha) = w - \sum_{i=1}^{N}\alpha_iy_ix_i = 0 $$
$$\bigtriangledown_b L(w,b,\alpha) = - \sum_{i=1}^{N}\alpha_iy_i = 0 $$
$$\alpha_{i}^{*}(y_i(w^{*}\cdot x_i + b^*) - 1) = 0, i=1,2,...,N$$
$$y_i(w^*\cdot x_i + b^*) - 1 \geq 0, i=1,2,...,N$$
$$\alpha_{i}^{*} \geq 0, i=1,2,...,N$$
支持向量:将训练数据及中对应于$\alpha_{i}^{*} > 0$的样本点$(x_i,y_i)$的实例$x_i \in R^n$称为支持向量。
问题:
(1)上述的对偶算法如何求解呢?请参考序列最小最优化算法
(2)对于线性可分问题,上述线性可分支持向量机的学习形式(硬间隔最大化)算法是完美的。但是,训练数据集线性可分是理想的情形。在现实问题中,训练数据集往往是线性不可分的,即在样本中出现噪声或特异点。此时,请参考线性支持向量机。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号