KMP算法详解

哈喽大家好，我是 doooge。今天给大家带来的是 KMP 算法的解析。

\[\Huge \sf 浅析 KMP 算法 \]

1.算法简介

首先我们要知道 KMP 是干什么的。先引入一个例题：

给定两个字符串 \(A\) 和 \(B\)，求出 \(A\) 有多少个子串和 \(B\) 相同，输出它们出现的位置。\(|B| \le |A| \le 5 \times 10^3\)。

这道题看上去很简单，因为 \(|A|\) 不超过 \(5000\)，那我们就可以用暴力来查找，也就是说枚举 \(A\) 中每一个字符作为起点，来判断是否能和 \(B\) 匹配，匹配完了后我们就可以移动字符串 \(B\) 到下一位，如果可以就输出答案。

例如，有两个字符串分别为 abacab 和 ab 那么匹配的过程就是：

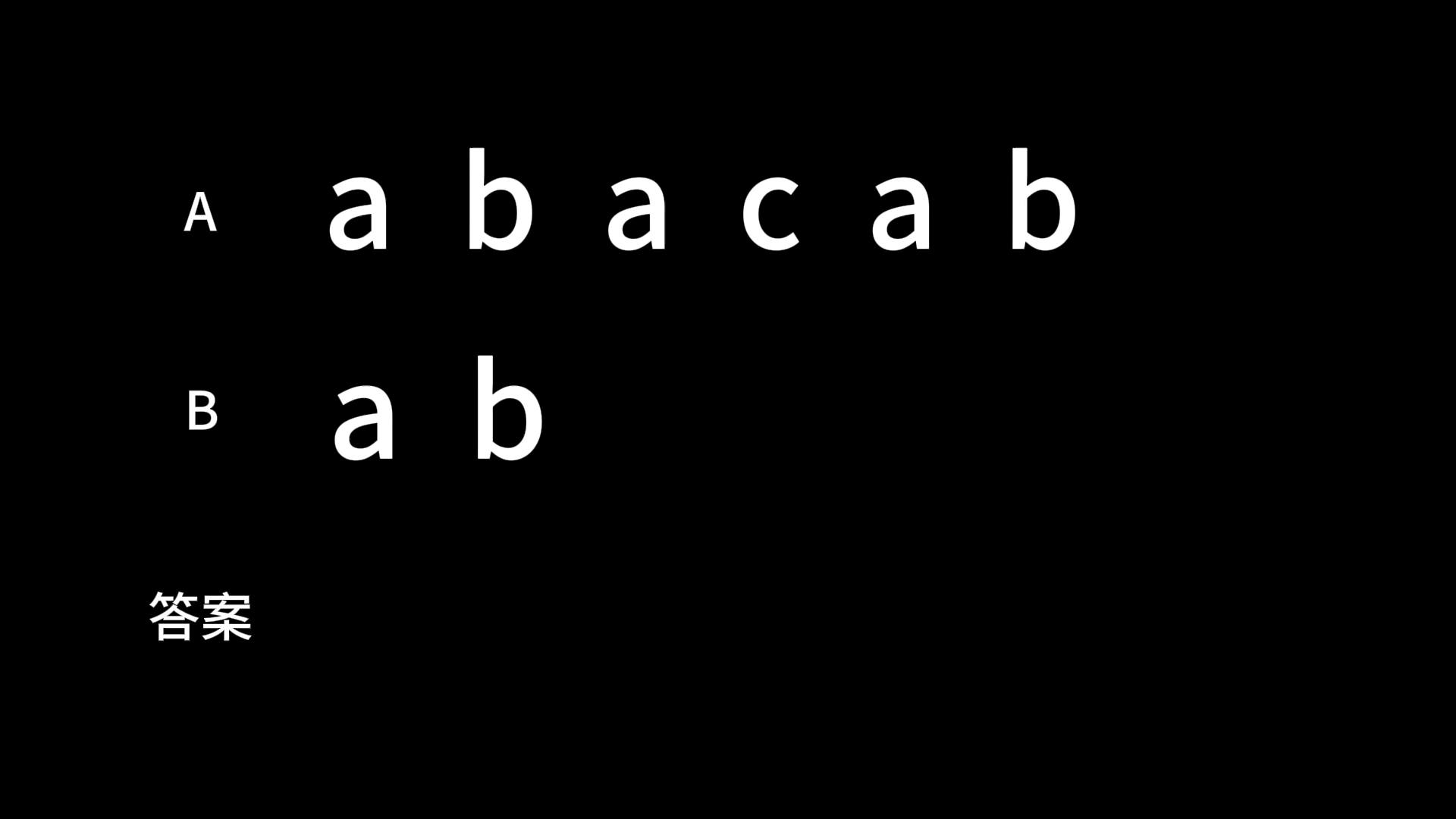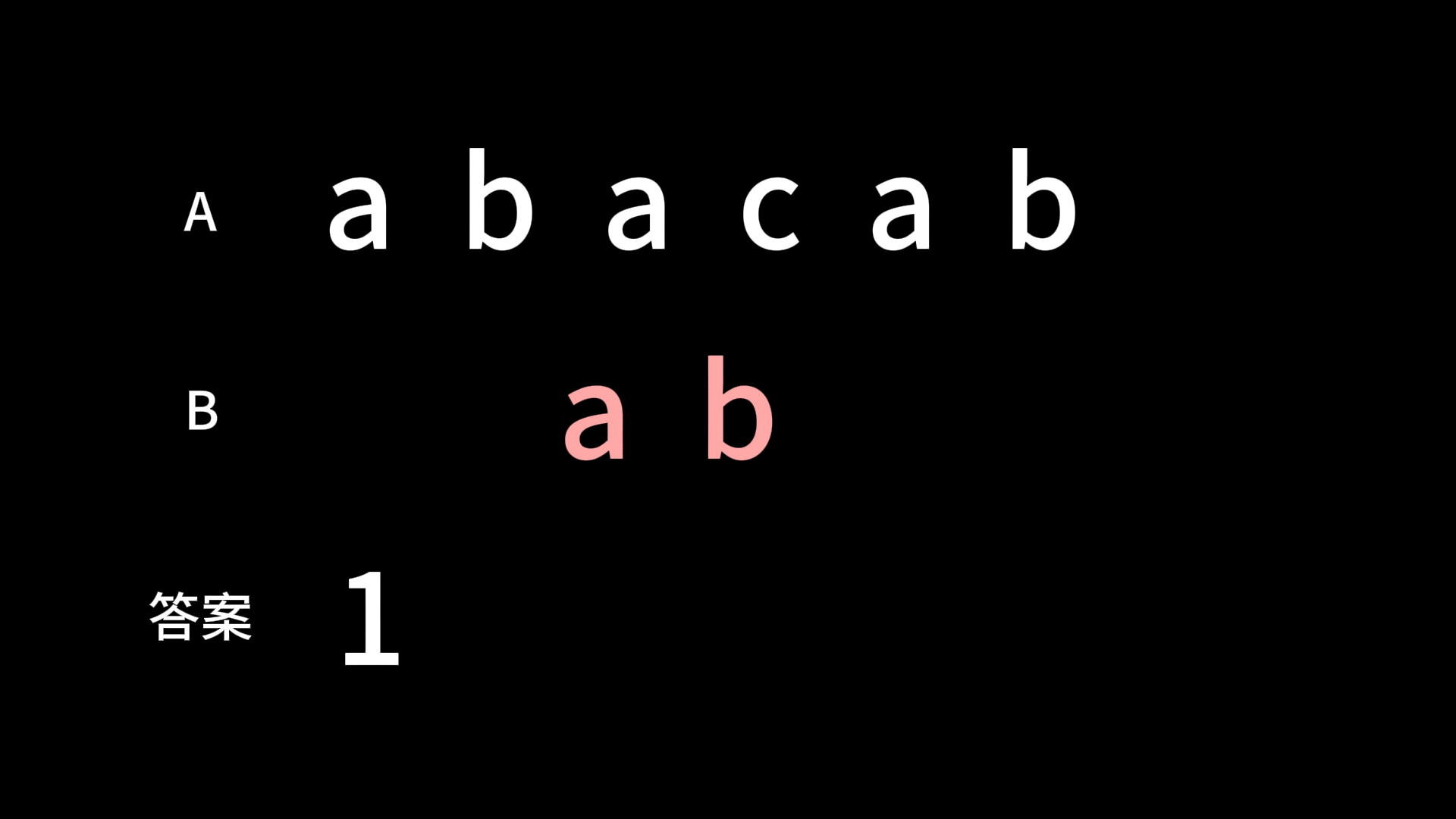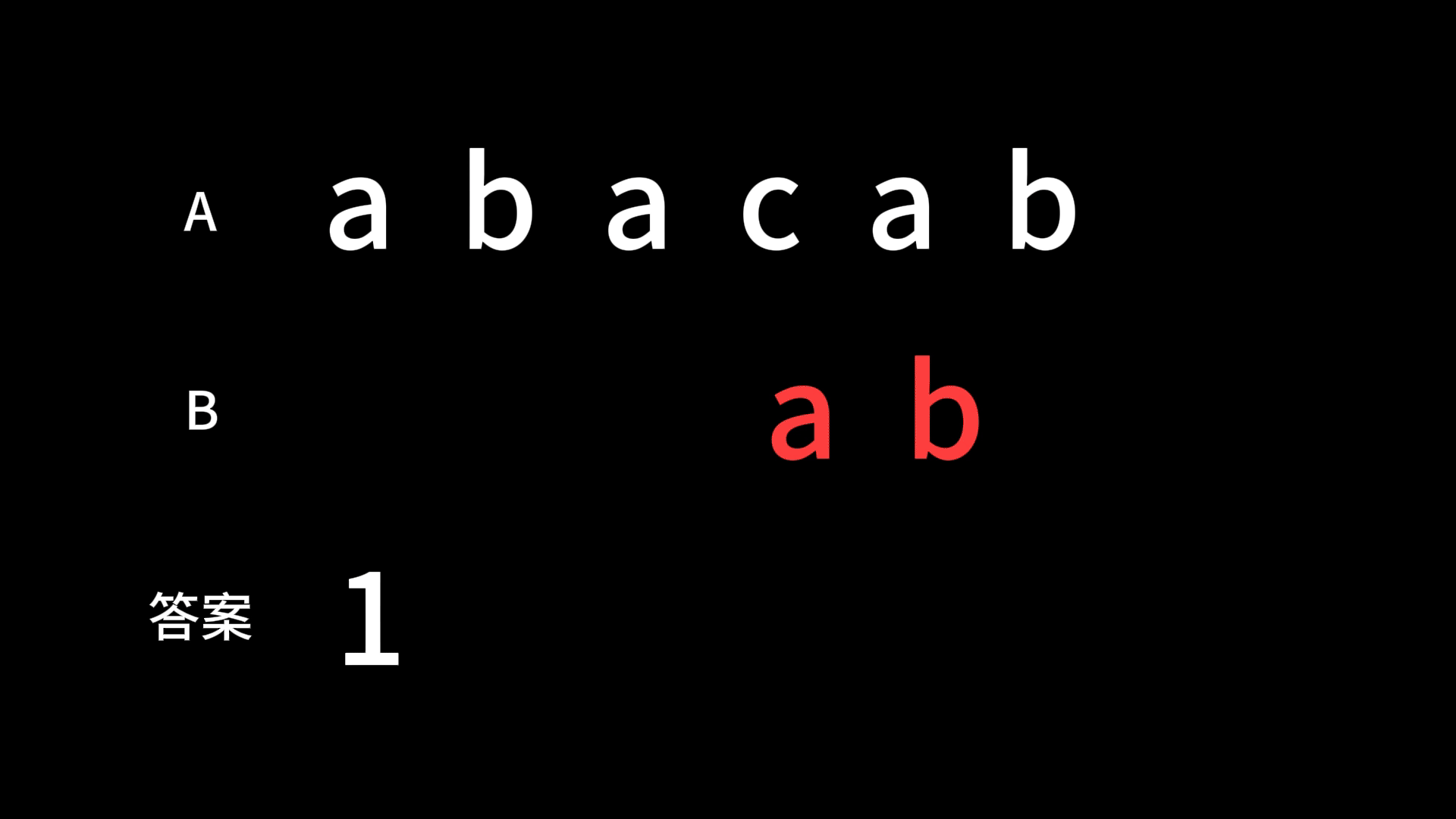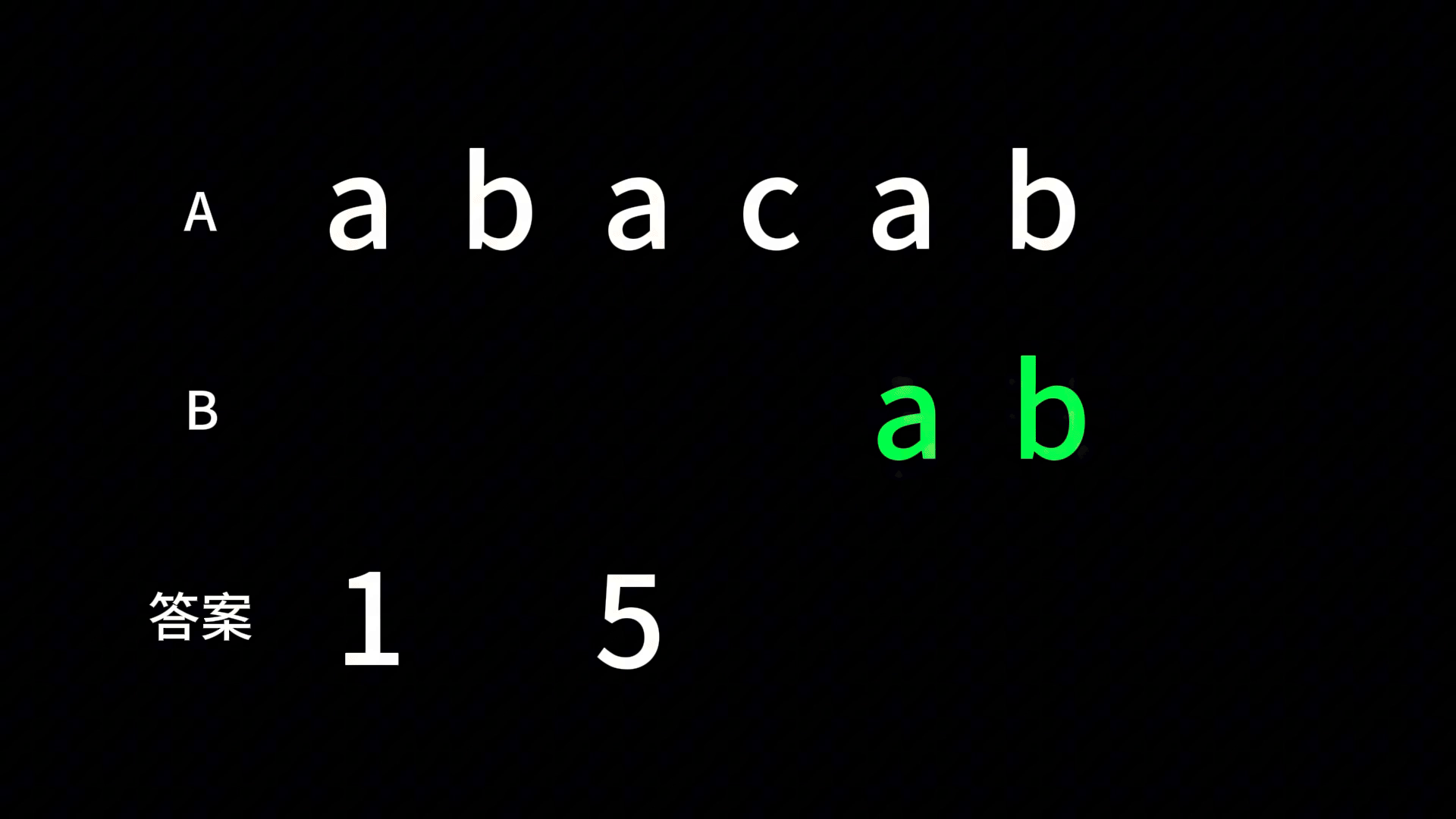
上代码：

for(int i=0;i<a.size()-b.size();i++){//防止越界
    bool flag=true;
    for(int j=i;j<i+b.size();j++){
        if(a[i]!=b[j]){
            flag=false;
            break;
        }
    }
    if(flag)cout<<i<<' ';
}

时间复杂度 \(O(|A| \cdot |B|)\)，也就是 \(O(n^2)\)。

2.正片：KMP算法的思想

我们还是给出这道题：

给定两个字符串 \(A\) 和 \(B\)，求出 \(A\) 有多少个子串和 \(B\) 相同，输出它们出现的位置。\(|B| \le |A| \le 10^6\)。
其实就是为了水字数

此时，\(O(n^2)\) 的暴力显然会挂掉除非你是欧皇每次刚开始匹配就结束，那么我们该如何应对这样丧心病狂的题目呢？

2.1 优化的思路

我们可以好好想想是从这个暴力哪里会让时间很长。我们可以逐个优化。我们用字符串 \(A\)，\(B\) 分别为 ABABABABC 和 ABABC 这两个字符串来模拟一下，我们需要一个指针 \(i\) 来记录比到了什么位置。

首先，我们先枚举从第 \(i\) 位开始后面的字符串是否相同，我们的指针 \(i\) 会从 \(1\) 扫到 \(4\)，此时的 \(A_i\) 都和 \(B_i\) 相同。但是当 \(i\) 扫到第 \(5\) 位时，由于 \(A_i\) 和 \(B_i\) 并不相同，所以第一次枚举失败。指针 \(i\) 会回到 \(2\) 来枚举第 \(2\) 位字符是否能成功匹配，由此循环往复。

我们会发现，正是这个回溯一样的操作才会使时间爆炸。尤其是这个毒瘤***钻的字符串 \(A\)，会让 \(i\) 指针傻傻的回退很多很多次，这样，我们就可以收获一个大大的 TLE 啦！

这肯定是不可能的。那我们有没有一种可以让指针 \(i\) 不往后退的算法呢？

于是，KMP 就这样诞生了！

2.2 优化后的算法

在暴力算法中，我们的 \(i\) 指针一直回退，才导致的超时的。

那么有什么可以让 \(i\) 指针不降呢？我们是否能从已经比较过的内容中找到一些线索呢？

比如说，有这么两个字符串 \(A\) 和 \(B\) 分别为 ABABABABC 和 ABABC，在第一次比较 ABABA 和 ABABC 时，我们会发现当指针 \(i\) 走到 \(5\) 时字符串不匹配，那么我们是否可以将 \(B\) 向后移动一定的距离，来达到 \(i\) 指针不下降的目的呢？请看下面：

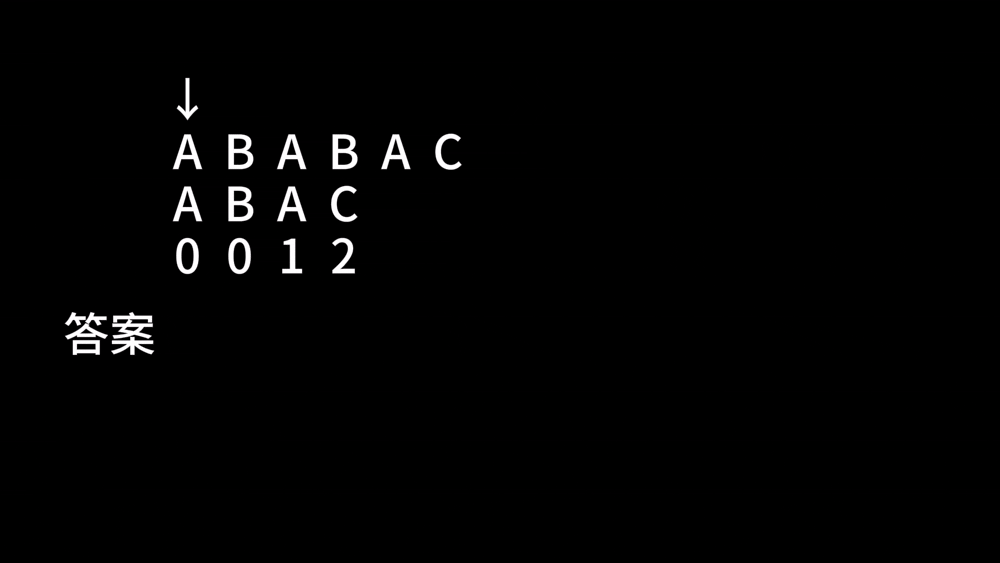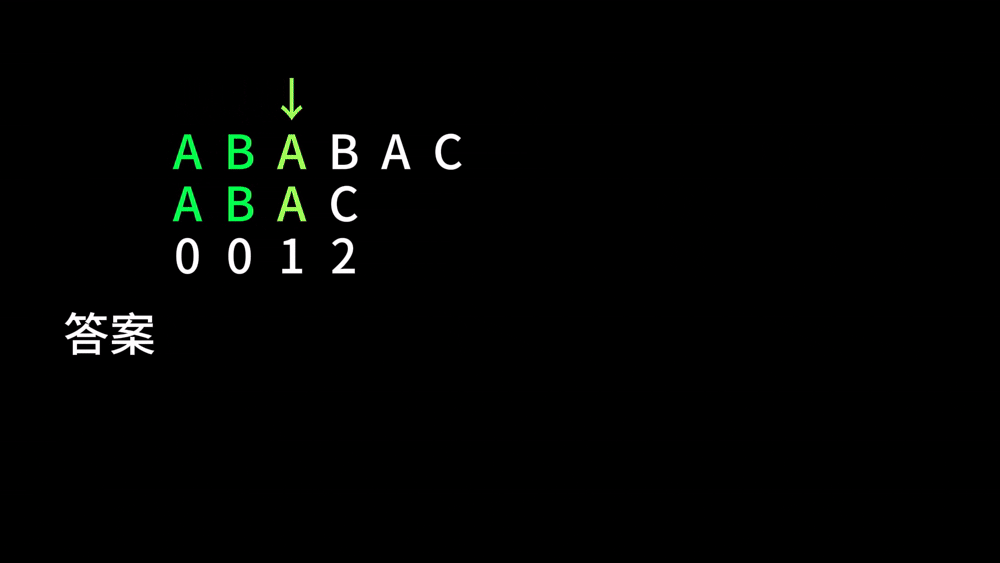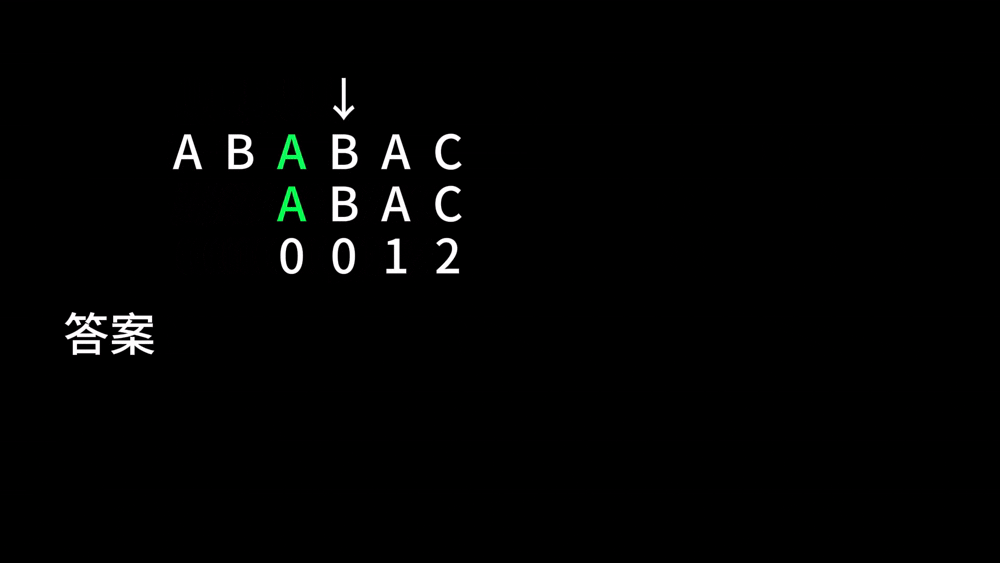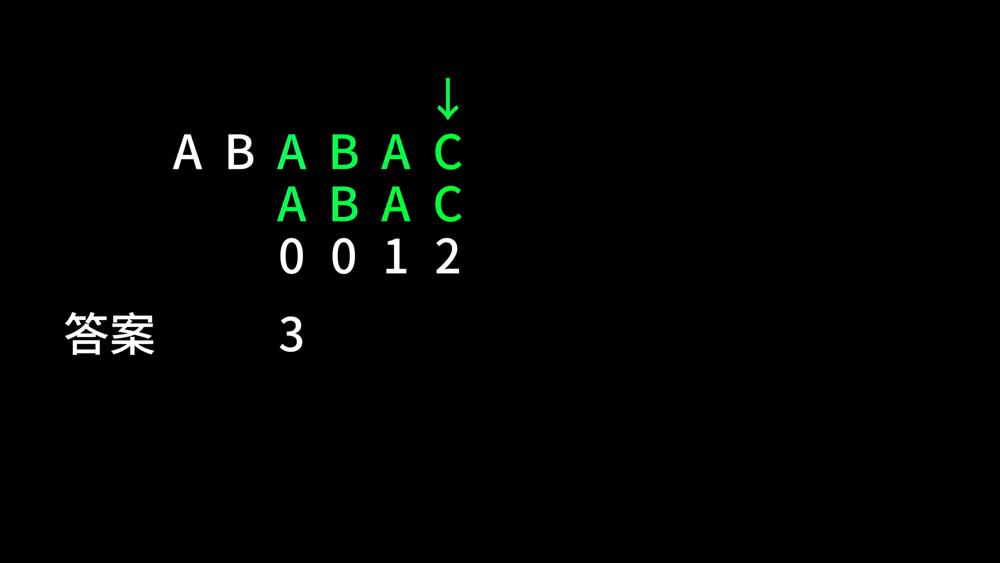
由于 \(B\) 串前面的 AB 和 \(A\) 串这里的 AB 是相同的，我们这样移位并没有什么问题。于是，我们就这样跳过了许许多多的比较，节省了非常多的时间。

那么我们怎么才能知道我们要跳过多少字符呢？我们可以用一个 \(next\) 数组来记录。我们先不用管 \(next\) 是怎么来的，用就完了。比如说上面的 \(B\) 串，其中每个下标 \(i\) 对应的 \(next_i\) 是这样的：

下标	1	2	3	4	5
字符串 \(B\) 中表示的值	\(A\)	\(B\)	\(A\)	\(B\)	\(A\)
对应的 \(next_i\)	\(0\)	\(0\)	\(1\)	\(2\)	\(3\)

可以自己去模拟一下。假设 \(|A|=n\)，\(|B|=m\)。

那么我们的查找的步骤就是：

1. 创建两个指针 \(i=1\) 和 \(j=0\)。
2. 如果 \(A_i=B_{j+1}\)，那么就说明可以继续匹配，将 \(i\) 和 \(j\) 分别加 \(1\)。
3. 重复执行 \(3 \sim 6\) 步直到 \(i=n\)。
4. 如果匹配失败，如果 \(j>0\)，使 \(j=next_{j-1}\)，看是否能够继续匹配，这一步最多执行 \(n\) 次。
5. 否则如果 \(j=0\)，从一开始就匹配失败了，直接将 \(i+1\)。
6. 如果 \(j=m\)，表示匹配成功，输出一开始的下标，也就是 \(i-j+1\)。

上代码（因为 c++ 中的变量名不能用 \(next\) 我也不知道为啥，于是我用 \(nxt\) 代替了一下）：

j=0;//初始化指针j=0
for(int i=0;i<n;){//指针i从0~n-1 
    if(s[i]==s2[j])i++,j++;//如果匹配成功就继续 
    else if(j>0)j=nxt[j-1];//否则就j=nxt[j-1]看是否能继续匹配 
    else i++;//如果从一开始就匹配不上就让指针i++ 
    if(j==m){//如果匹配成功 
        cout<<i-j+1<<'\n';//输出开始匹配的位置i-j+1 
        j=nxt[j-1];//j=nxt[j-1]一边继续匹配 
    }
}

那我们应该如何求 \(next\) 数组呢？请往下看。

2.2 公共前缀后缀（border）

首先说明一下，\(S_{i \to j}\) 表示 \(S\) 中下标为 \(i\) 到 \(j\) 的子串。

正如题目所述，\(S\) 的 border 表示 \(S\) 的公共的前缀和后缀，\(S\) 的最长的 border 表示 \(S\) 的最长的公共的前缀和后缀。\(S\) 的前缀和后缀相信大家都知道吧，abcab 的前缀有 a，ab，abc 等等，而后缀有 b，ab，cab 等等。

比如说，如果 \(S\) 为 abcabc，那么 \(S\) 的 border 只有一个，就是 abc，因为 \(S\) 的前缀和后缀中分别都有 abc 这个字符串。特别的，\(S\) 本身并不是一个 border，也就是 aaa 不是 aaa 的 border，只有 a 和 aa 才是。

那么这跟 \(next\) 数组有什么关系呢？

我们可以分析一下 \(next\)，拿一个例子：

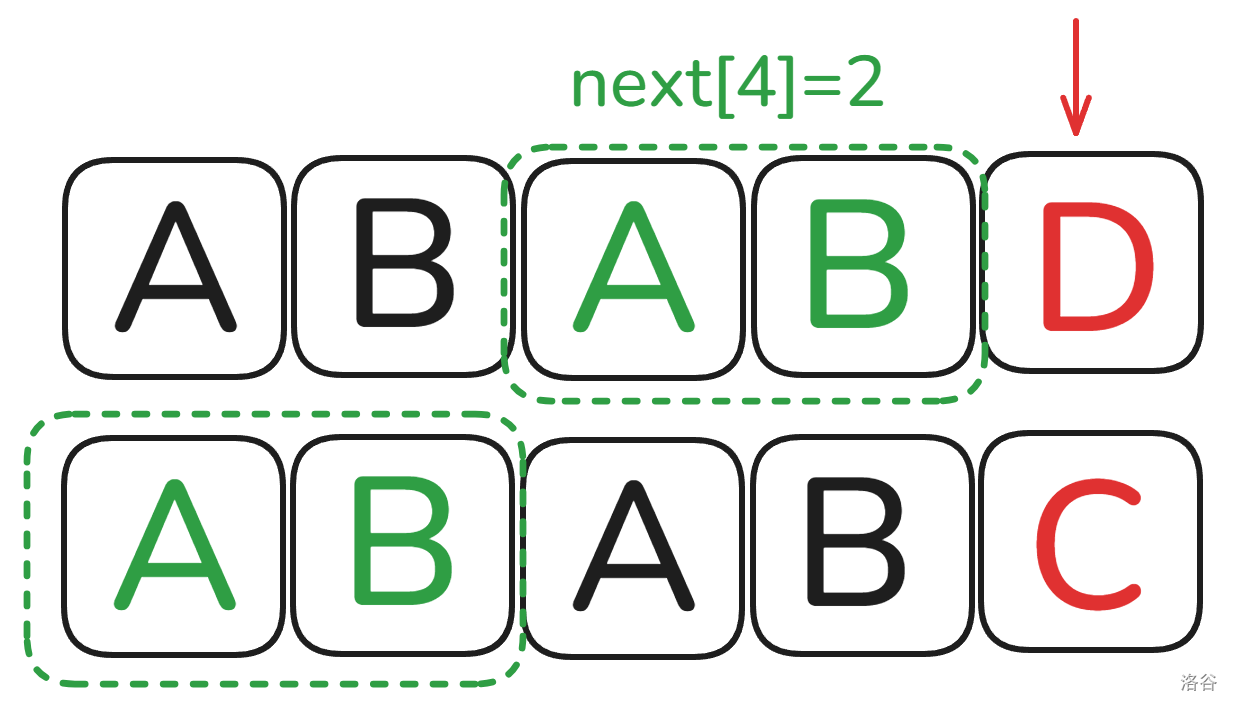
稍微转变一下：

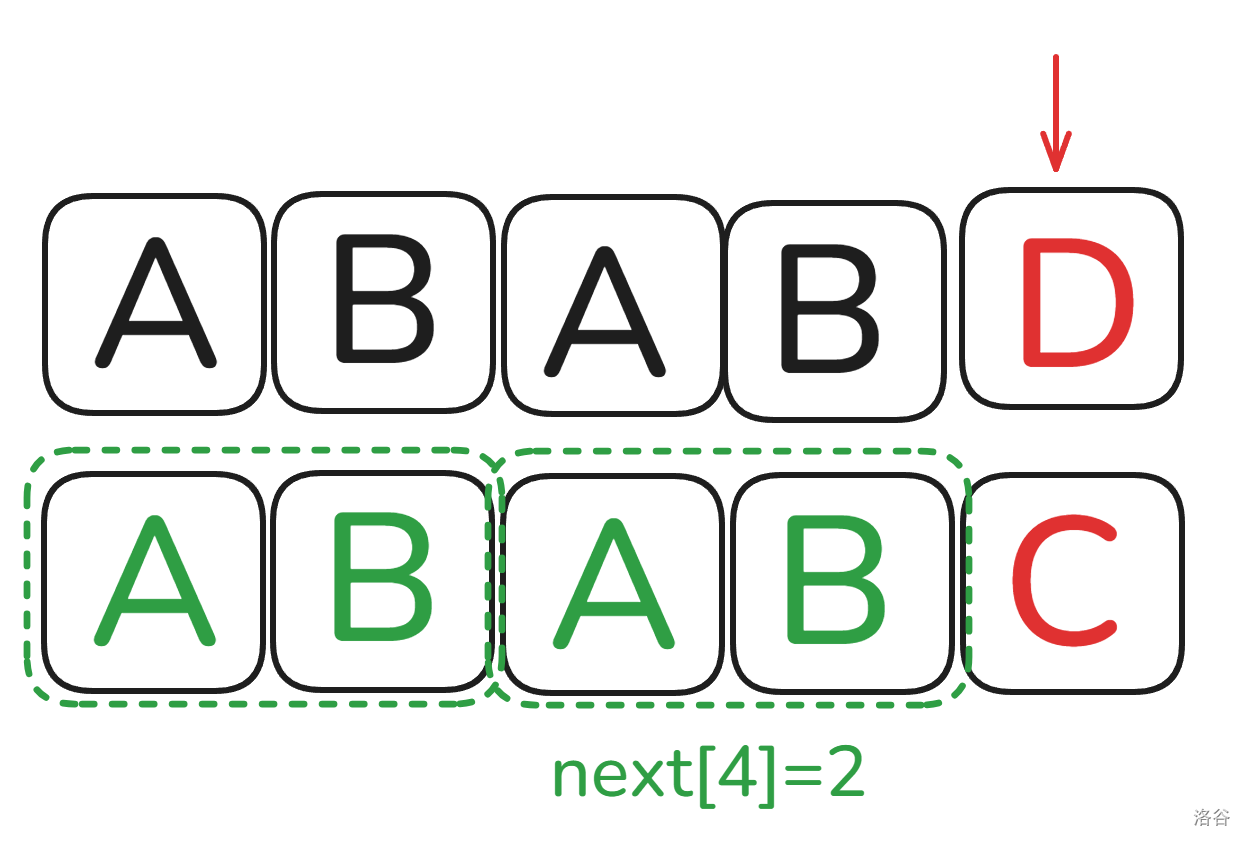
再把不相关的东西给去掉：

诶！这个东西好像就是刚刚说的最长的公共前缀后缀吗？

没错，这就是 \(next\) 的核心求法，我们在举个例子详细说一说，设上面的字符串为 \(A\)，下面的字符串为 \(B\)：

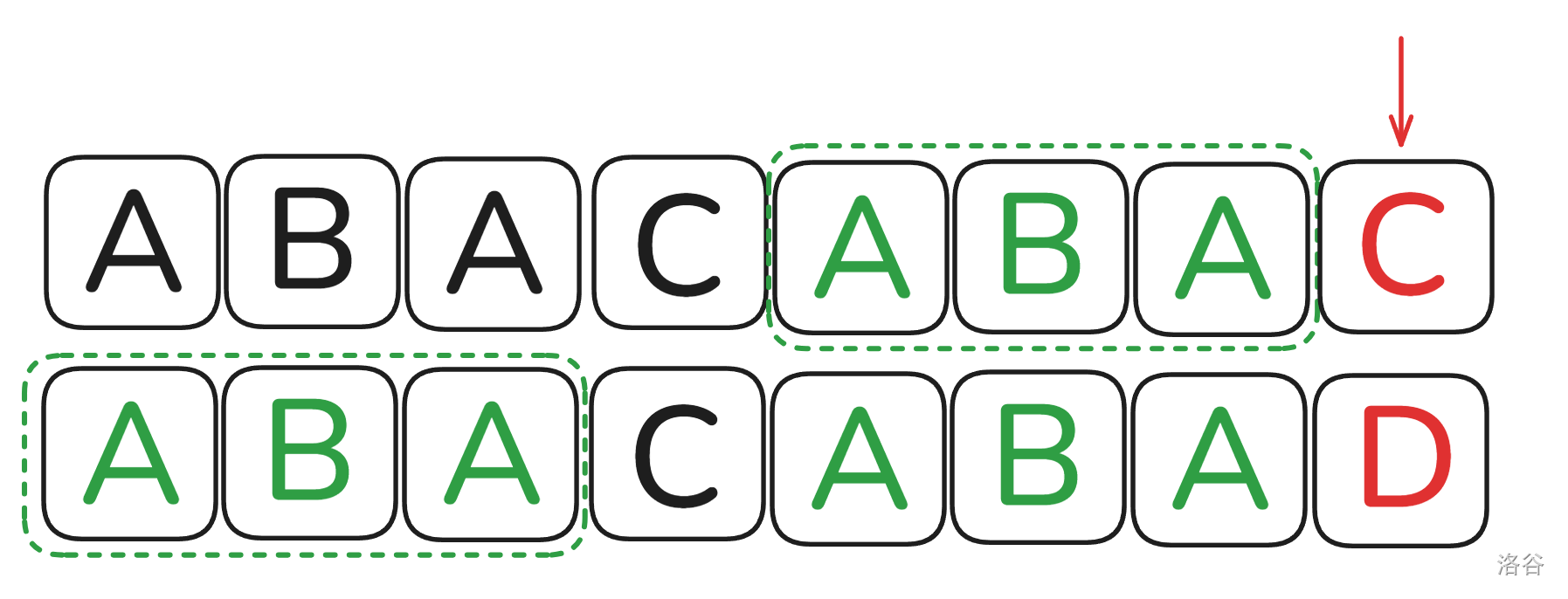
当我们发现匹配不上时，为了找到所有潜在的答案，所以因该找到一个最靠左边且可能可以重新匹配的下标。比如说炸这幅图中最小的下标是 \(4\)。而如果从 \(4\) 开始匹配，能匹配 \(3\) 个字符，也就是 \(B_{1 \to 3}\) 这一段子串，进而我们就能得知 \(next_7=3\)。

那为什么是 \(3\) 呢？我们可以先把刚刚已经匹配的 \(A\) 的部分移下来。

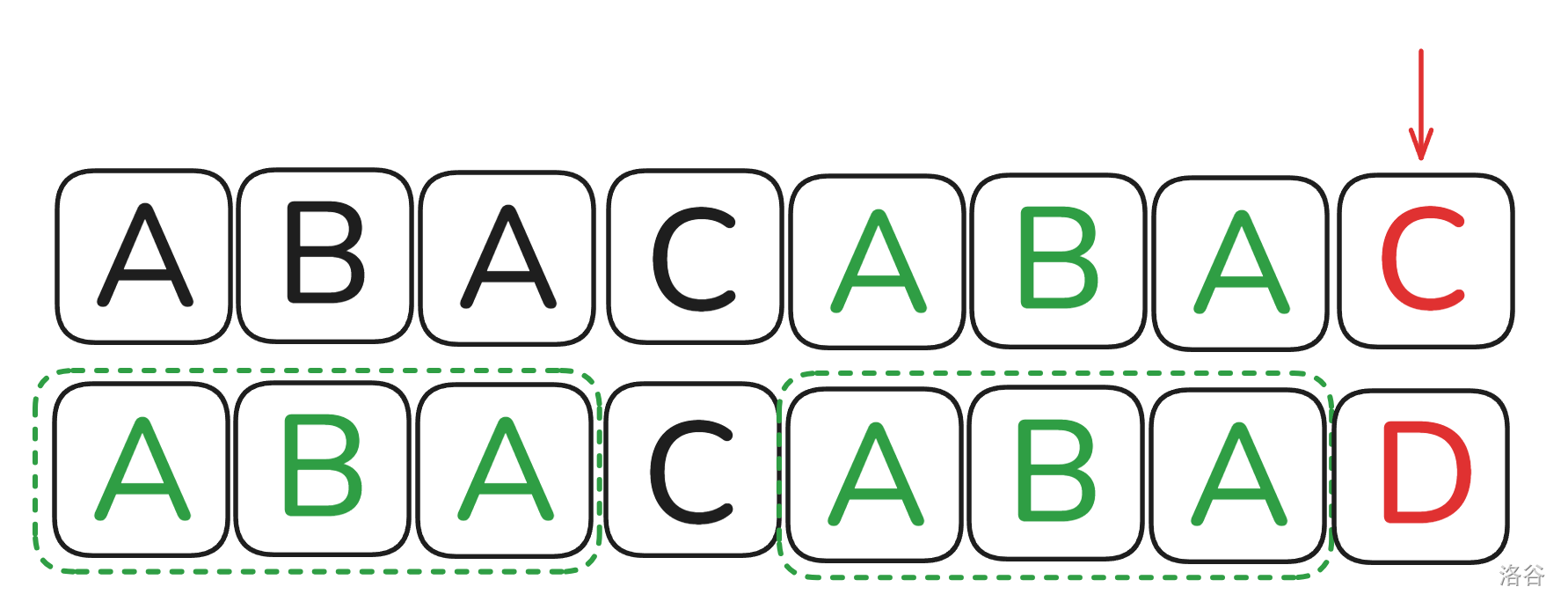
此时我们需要最小可以重新匹配的坐标，也就是 \(B\) 字符串右边这一段长度最大，那我们可以推回去。因为 \(B\) 字符串右边这一段，也就是 \(A\) 字符串右边这一段，又因为我们要找的是重新匹配的位置，所以也就是从 \(B\) 的第一项开始匹配，也就是说，我们想要求出最左边可以重新匹配的下标，也就是需要最长的长度 \(x\) 使 \(B_{1 \to x}=B_{i-x+1 \to i}\)，也就是 \(B\) 的最长的公共前缀后缀。

如此，我们就可以用求出 \(S_{1 \to i}\) 的最长公共前缀后缀的长度来计算 \(next\) 数组了。

2.3 next数组的求法

如果我们用暴力求解 \(next\) 数组，时间复杂度很差，因为我们对于每一个下标 \(i\) 都要求一遍 \(next_i\)，这需要枚举长度然后再根据长度来判断，时间复杂度 \(O(n^3)\)，实在太差，有这时间还不如去打暴力呢。

当然，这个求法有很大的改进空间，我们可以一步一步优化它。

2.4 next求法优化

显然，我们需要优化 \(next\) 数组的求法过程。

我们在求解 \(next_i\) 时，显然已知 \(next_1\) 到 \(next_{i-1}\)，我们应该从已经求出 \(next\) 数组的值来求出 \(next_i\) 这是什么废话。

想想，\(S_{1 \to i-1}\) 与 \(S_{1 \to i}\) 只差了 \(S_i\) 这一个字符，然而我们又知道 \(S_{i-next_{i-1} \to i-1}=S_{1 \to next_{i-1}}\)，也就是 \(S\) 下标 \(i-1\) 的最长后缀等于最长前缀，那我们可不可以继承 \(next_{i-1}\) 求出 \(next_i\) 呢？请看下图：

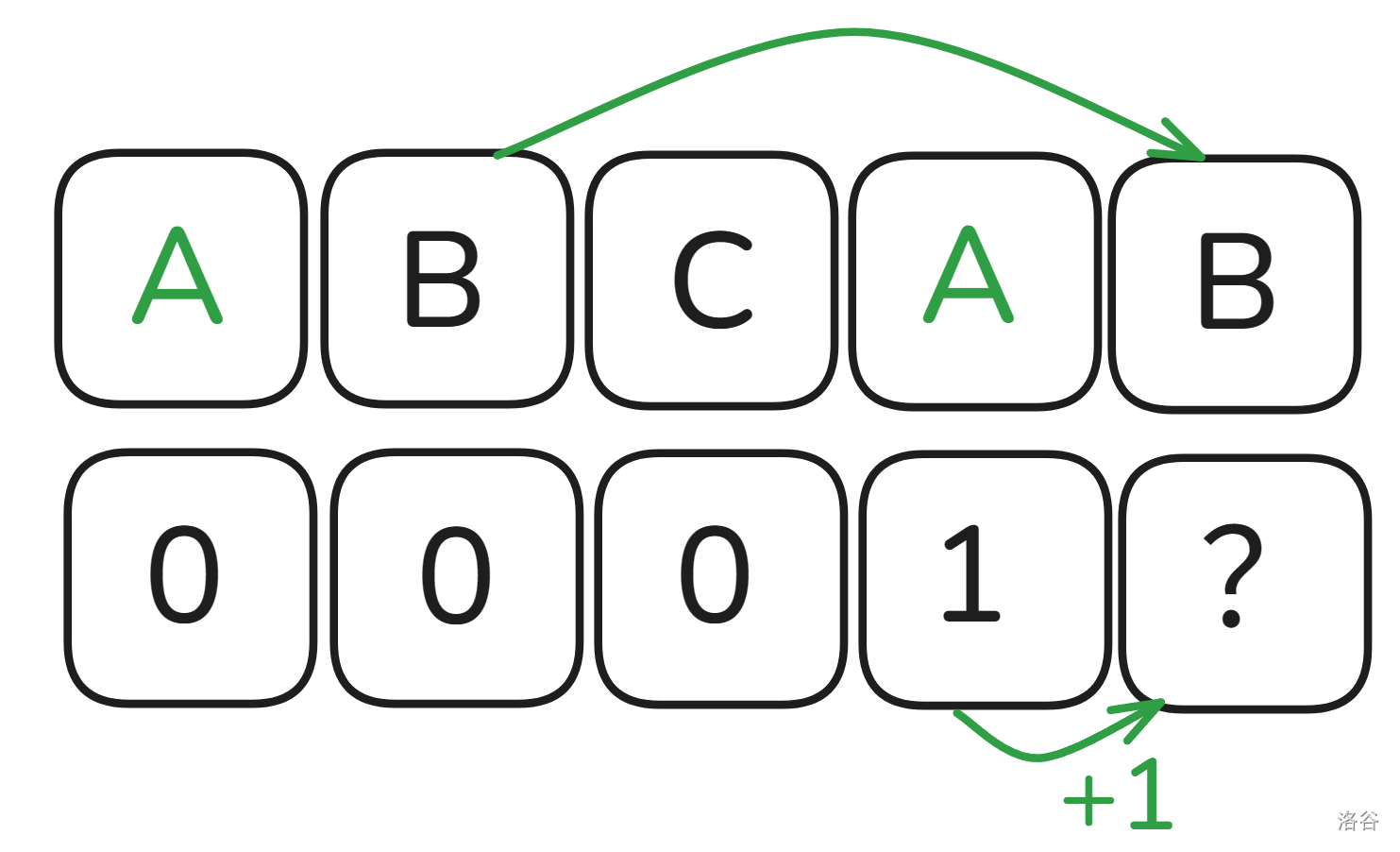
所以，当 \(S_i=S_{next_{i-1}+1}\) 时，\(next_i\) 就能继承 \(next_{i-1}\)。

但是这还不够，如果 \(S_i \not = S_{next_{i-1}+1}\) 时，我们应该怎么办呢？不会又要回到之前的暴力求解了吧。

不如我们来看下面的例子：

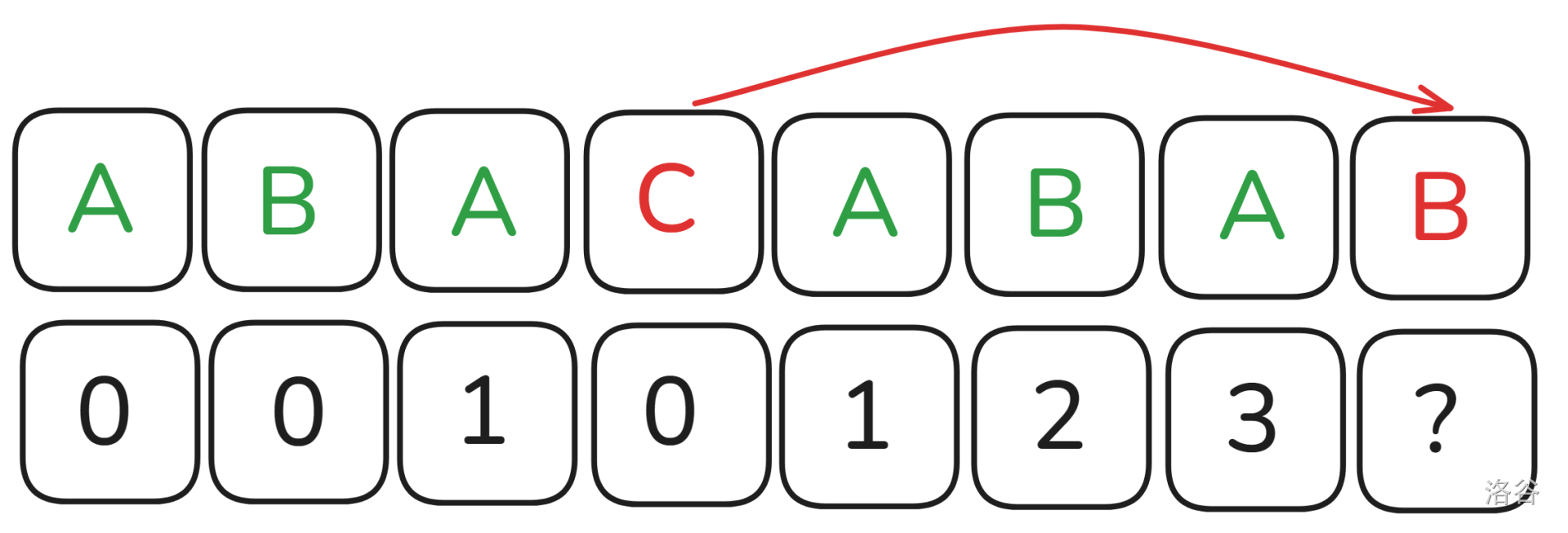
我们会发现，虽然匹配不成功，但是 \(next_i\) 可以从开头的 \(AB\) 转移过来。

那我们应该怎么知道 \(next_i\) 是从开头的 \(AB\) 转移过来呢？

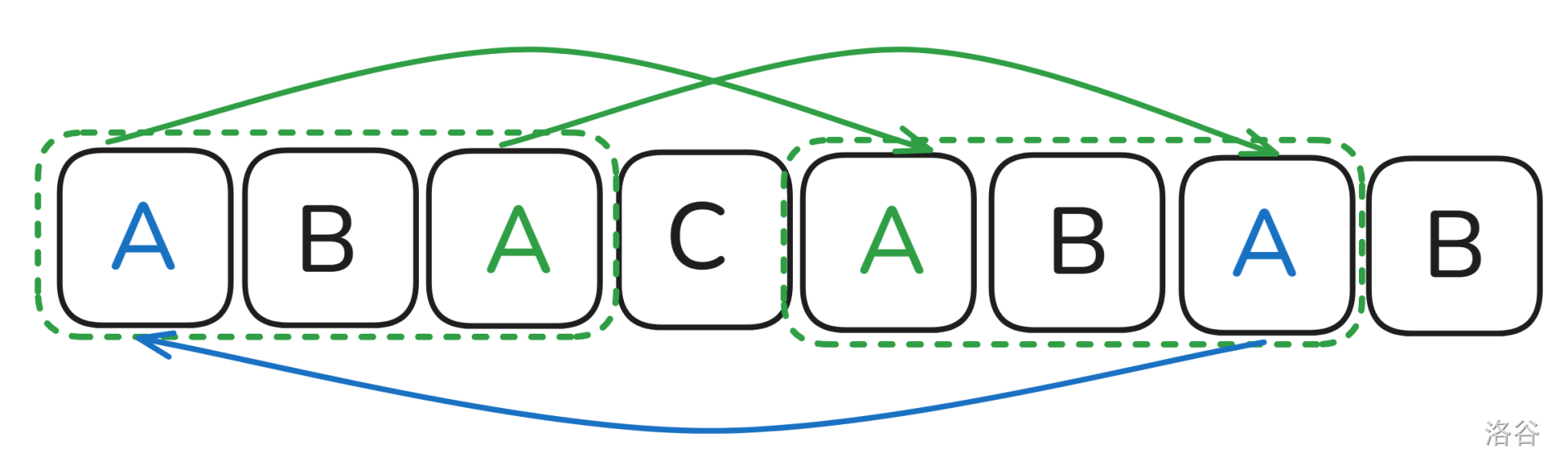
我们知道，\(S_{1 \to i-1}\) 的前缀子串和后缀子串是相等的，那么是不是 \(S_{1 \to i-1}\) 的前缀子串的前缀子串和后缀子串的后缀子串是相等的？

这句话虽然有点绕，但是从上面的图片不难看出，\(next_i\) 可以从 \(next_{next_{i-1}}\) 转移过来，也就是如果 \(S_i=S_{next_{next_{i-1}}+1}\) 时，\(next_i\) 就能从 \(next_{next_{i-1}}\) 转移过来。不难发现，我们可以如此递归（设目前 \(next_i\) 的长度为 \(len\)）\(len=next_{len-1}\)，直到 \(S_i=S_len\) 或 \(len=0\) 为止。

综上所述，\(next_i\) 可以这样转移，我们设目前的下标 \(i=1\) 和目前的长度 \(len=0\)：

• 如果 \(S_i=S_{len}\)，那么 \(next_i=len\)，将 \(i\) 和 \(len\) 增加 \(1\)。
• 否则，如果 \(len=0\)，那么 \(next_i=len\)，将 \(i\) 增加 \(1\)。
• 否则，将 \(len\) 变为 \(next_{len-1}\)，递归下去。

不难发现，递归次数不会大于 \(|S|\) 次。于是，我们将求 \(next\) 数组的复杂度降为了 \(O(n)\)。

所以，写出 KMP 的代码就不难了吧！

3.KMP算法的代码

P3375 【模板】KMP

#include<bits/stdc++.h>
using namespace std;
int nxt[1000010],n,m,len,j;
string s,s2;
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
	cin>>s>>s2;
    n=s.size(),m=s2.size();
    for(int i=1;i<m;){
        if(s2[i]==s2[len]){
            nxt[i]=++len;
            i++;
        }else{
            if(len==0){
                nxt[i]=0;
                i++;
            }else len=nxt[len-1];
        }
    }
    j=0;
    for(int i=0;i<n;){
        if(s[i]==s2[j])i++,j++;
        else if(j>0)j=nxt[j-1];
        else i++;
        if(j==m){
        	cout<<i-j+1<<'\n';
        	j=nxt[j-1];
    	}
    }
	for(int i=0;i<s2.size();i++){
        cout<<nxt[i]<<' ';
    }
	cout<<endl;
	return 0;
}

4.闲话

蒟蒻不才，膜拜大佬，如果文章有任何的错字等问题，请在评论区 @我。

感谢这个视频教会了我KMP，也推荐大家都去学一学，讲的很详细：最浅显易懂的 KMP 算法讲解。