树形DP详解

哈喽大家好，我是 doooge，今天给大家带来的是树形DP 详解。

\[\Huge \sf 树形DP 详解 \]

1.树形DP是什么

想必大家都学过动态规划吧，树形DP 就是 DP 的一部分。顾名思义，树形DP 就是在树上做动态规划。

2.树形DP的转移

知道了树形DP 是什么后，想必聪明的读者肯定想问：在树上怎么才能转移 \(dp\) 数组呢？

我们可以想想，不难想出，有两个转移的方法：

父节点转移到子节点，这种更新方法一般作为树上链路问题，比如说求每个节点的深度可以用 \(dp_x=dp_{fa}+1\) 来更新。
子节点转移到父节点，这种更新方法一般用于树上选点问题（详见两道例题）。

这两种转移方法的代码也很好写。

子节点转移父节点：
写法跟树上 DFS 一样：

for(auto i:v[x]){
    if(i==fa)continue;
    dfs(i,x);//继续dfs
    //dp[x]=dp[i]...转移
}

父节点转移子节点：
```
//dp[x]=dp[fa]...转移
```

3.树形DP 的例题

3.1 P1122 最大子树和

3.1.1 题目描述

小明对数学饱有兴趣，并且是个勤奋好学的学生，总是在课后留在教室向老师请教一些问题。一天他早晨骑车去上课，路上见到一个老伯正在修剪花花草草，顿时想到了一个有关修剪花卉的问题。于是当日课后，小明就向老师提出了这个问题：

一株奇怪的花卉，上面共连有 \(n\) 朵花，共有 \(n-1\) 条枝干将花儿连在一起，并且未修剪时每朵花都不是孤立的。每朵花都有一个“美丽指数”，该数越大说明这朵花越漂亮，也有“美丽指数”为负数的，说明这朵花看着都让人恶心。所谓“修剪”，意为：去掉其中的一条枝条，这样一株花就成了两株，扔掉其中一株。经过一系列“修剪“之后，还剩下最后一株花（也可能是一朵）。老师的任务就是：通过一系列“修剪”（也可以什么“修剪”都不进行），使剩下的那株（那朵）花卉上所有花朵的“美丽指数”之和最大。

老师想了一会儿，给出了正解。小明见问题被轻易攻破，相当不爽，于是又拿来问你。

3.1.2 思路

咳咳，这道题的题面稍微有点乱，我来简化一下：

有一棵树，每个点都有点权，你可以去掉该树的一些子树，使剩余部分的点权和最大

直接考虑树形DP 怎么写。

不难想到，\(dp_x\) 表示子树 \(x\) 去掉部分子树最大的点权和。首先肯定的，\(dp_x=a_x\)，也就是必须选自己。

那我们怎么转移呢？

因为是要选择子树，所以肯定 \(dp_x\) 肯定是从 \(x\) 的子树转移而来的。我们设 \(x\) 的子树为 \(i\)，因为点 \(i\) 的点权可能为负，\(dp_i\) 也可能为负，我们既然想要选择最有的子树，也就是要选择点权和大于 \(0\) 的子树，所以可以得到 \(dp_x=\max(dp_x,dp_x+dp_i)\)。

放在代码上也就是：

for(auto i:v[x]){
    if(i==fa)continue;
    dfs(i,x);
    dp[x]=max(dp[x],dp[x]+dp[i]);
}

当然我们也知道，当 \(dp_x>0\) 时，\(dp_x+dp_i\) 肯定会大于 \(dp_x\)，所以代码也可以写成：

for(auto i:v[x]){
    if(i==fa)continue;
    dfs(i,x);
    if(dp[i]>0)dp[x]+=dp[i];
}

当然，不要忘了初始化 \(dp_x=a_x\)，整个 DFS 代码也就出来了：

void dfs(int x,int fa){
	dp[x]=a[x];
	for(auto i:v[x]){
		if(i==fa)continue;
		dfs(i,x);
		if(dp[i]>0)dp[x]+=dp[i];
	}
	return;
}

相信读者如果会了 DFS 的代码，完整代码也不难了吧！

3.1.3 代码

代码：

#include<bits/stdc++.h>
using namespace std;
int dp[100010],a[100010];
vector<int>v[100010];
void dfs(int x,int fa){
	dp[x]=a[x];
	for(auto i:v[x]){
		if(i==fa)continue;
		dfs(i,x);
		if(dp[i]>0)dp[x]+=dp[i];
	}
	return;
}
int main(){
	int n,ans=-1e18;
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	for(int i=1;i<n;i++){
		int x,y;
		cin>>x>>y;
		v[x].push_back(y);
		v[y].push_back(x);
	}
	dfs(1,-1);
	for(int i=1;i<=n;i++){
		ans=max(ans,dp[i]);
	}
	cout<<ans<<endl;
	return 0;
}

3.2 P1352 没有上司的舞会

某大学有 \(n\) 个职员，编号为 \(1\ldots n\)。

他们之间有从属关系，也就是说他们的关系就像一棵以校长为根的树，父结点就是子结点的直接上司。

现在有个周年庆宴会，宴会每邀请来一个职员都会增加一定的快乐指数 \(r_i\)，但是呢，如果某个职员的直接上司来参加舞会了，那么这个职员就无论如何也不肯来参加舞会了。

所以，请你编程计算，邀请哪些职员可以使快乐指数最大，求最大的快乐指数。

3.2.2 思路

这道题的题面并没有多长，所以就不做简化题意了~~其实是我懒~~。

我们同样考虑树形DP 怎么写，这道题的情况就比较复杂了。

先不管别的，我们设 \(dp_x\) 表示选了 \(x\) 职员，在 \(x\) 职员关系的子树内所能达成的最大快乐值。我们考虑怎么转移。

这个时候我们会发现，转移并不好写，因为我们选择了 \(x\)，那么 \(x\) 的父节点和子节点都选不了。也就是说得要从这样才能转移过来：

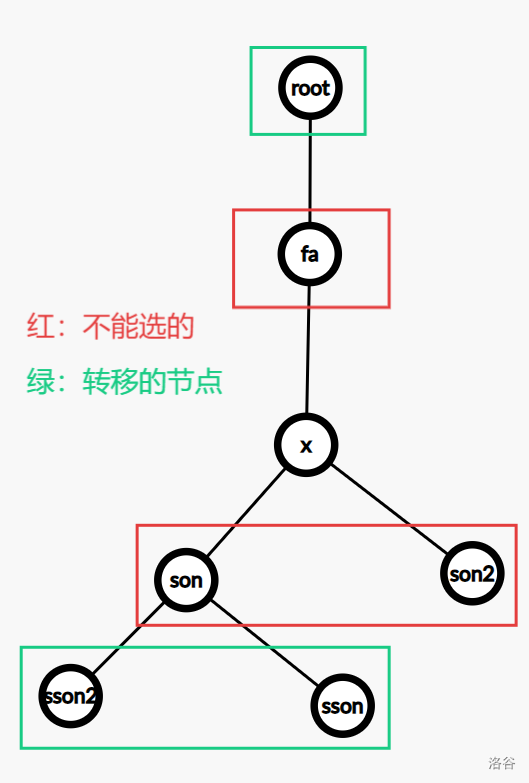
这样不仅难写，还容易写错。

我们重新想想：如果选择了 \(i\)，如果选择了 \(i\)，就不能选择 \(i\) 相邻的节点。那我们可不可以设计一个状态表示不选 \(i\)，包括 \(i\) 的子树最大的快乐值。这样转移也好写多了。

于是！我们可以增加一维状态 \(1\) 和 \(0\) 来表示选或不选的最大快乐值，转移，但是需要注意，有些职员的快乐值为负~~大概是整顿职场的吧~~，我们还要对自己取 \(\max\)。

\(dp_{x,1}\) 因为选了自己，必须不选子节点，所以：

\(dp_{x,1}=\max(dp_{x,1},dp_{x,1}+dp_{i,1})\)

然而 \(dp_{x,0}\) 因为没有选自己，选不选子节点都没问题，所以：

\(dp_{x,0}=\max(dp_{x,0},dp_{x,0}+\max(dp_{i,0},dp_{i,1}))\)

转移的代码也就很好写了，在这里就不多细讲了。

3.2.3 代码

代码：

#include<bits/stdc++.h>
using namespace std;
int a[100010],dp[100010][5];
vector<int>v[100010];
void dfs(int x,int fa){
	dp[x][1]=a[x];
	for(int i:v[x]){
		if(i==fa)continue;
		dfs(i,x);
		dp[x][1]+=max(0,dp[i][0]);
		dp[x][0]+=max(0,max(dp[i][0],dp[i][1]));
	}
	return;
}
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=1;i<n;i++){
		int x,y;
		cin>>x>>y;
		v[x].push_back(y);
		v[y].push_back(x);
	}
	dfs(1,-1);
	cout<<max(dp[1][0],dp[1][1])<<endl;
	return 0;
}

什么？你说~~你不想在这里~~这些题太简单了？别急嘛，这还有更难的等着你呢

3.3 P2585 [ZJOI2006] 三色二叉树

3.3.1 题目描述

一棵二叉树可以按照如下规则表示成一个由 \(0\)、\(1\)、\(2\) 组成的字符序列，我们称之为“二叉树序列 \(S\)”：

\[S= \begin{cases} 0& \text表示该树没有子节点\\ 1S_1& 表示该树有一个节点，S_1 为其子树的二叉树序列\\ 2S_1S_2& 表示该树有两个子节点，S_1 和 S_2 分别表示其两个子树的二叉树序列 \end{cases}\]

例如，下图所表示的二叉树可以用二叉树序列 \(S=\texttt{21200110}\) 来表示。

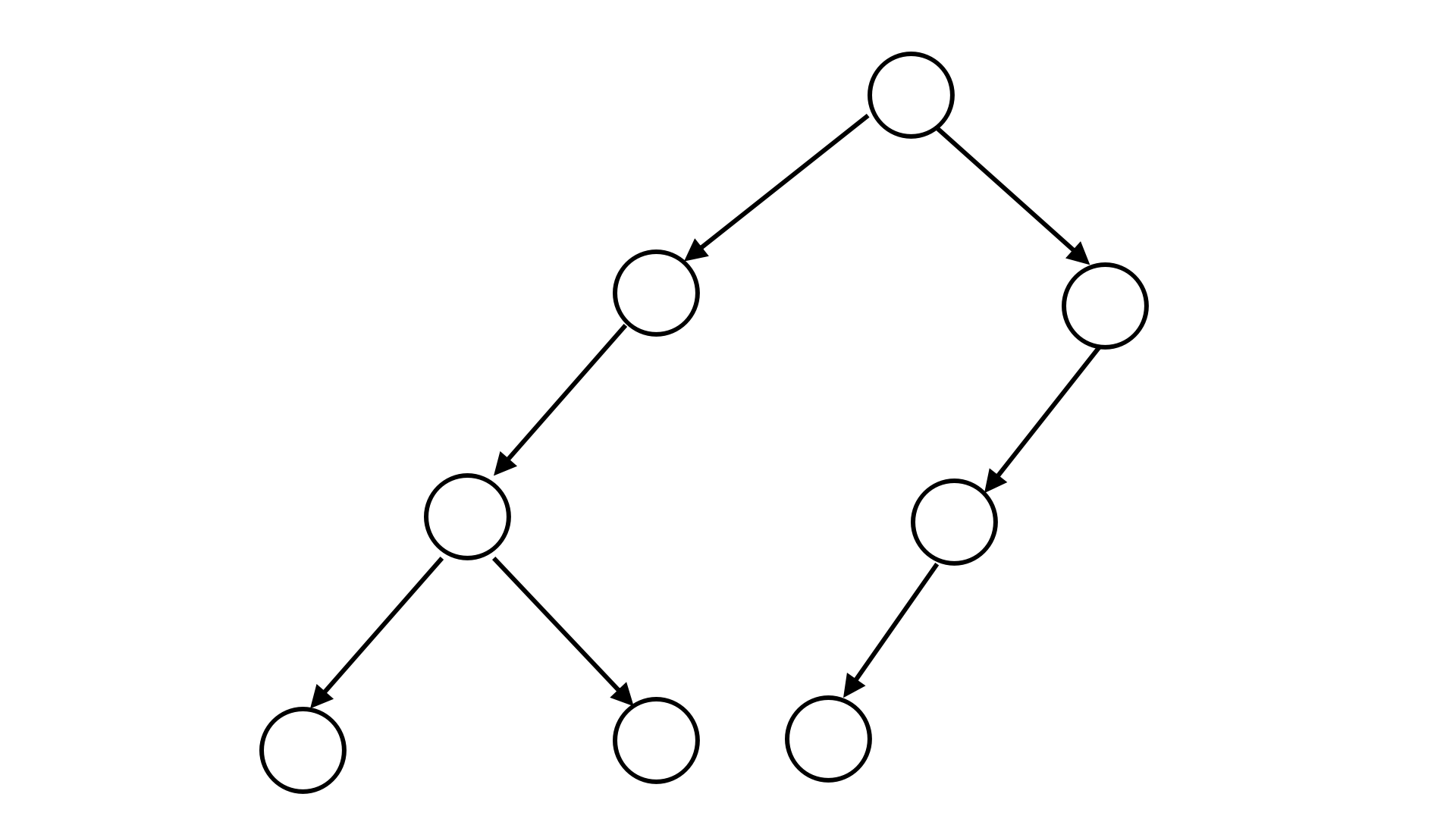
你的任务是要对一棵二叉树的节点进行染色。每个节点可以被染成红色、绿色或蓝色。并且，一个节点与其子节点的颜色必须不同，如果该节点有两个子节点，那么这两个子节点的颜色也必须不同。给定一颗二叉树的二叉树序列，请求出这棵树中最多和最少有多少个点能够被染成绿色。

3.3.2 思路

我们先来考虑要求最大值该怎么写。

因为染绿色蓝色和红色都是一样的，所以我们求染绿色蓝色红色都是一样的。

于是我们可以设 \(dp_{x,1}\)，\(dp_{x,2}\) 和 \(dp_{x,3}\) 为 \(x\) 节点染绿色，红色和蓝色，\(x\) 及所在的子树中的绿色节点最大的个数。

接下来想想如何转移，我们可以先想想将 \(x\) 染成绿色，子节点可以怎么染，如图：

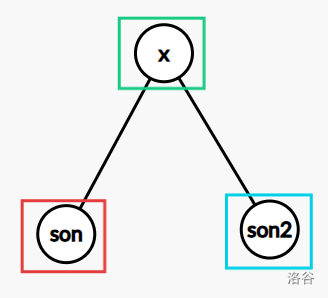
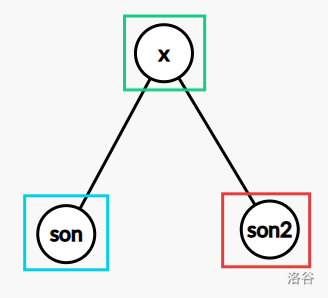
因为这题是个二叉树，如果我们把左儿子表示成 \(ls\)，右儿子表示成 \(rs\)，转移应该这样：

\[dp_{x,1}=\max(dp_{ls,2}+dp_{rs,3},dp_{ls,3}+dp_{rs,2}) \]

同样，我们也能得到：

\[dp_{x,2}=\max(dp_{ls,1}+dp_{rs,3},dp_{ls,3}+dp_{rs,1}) \]

\[dp_{x,3}=\max(dp_{ls,1}+dp_{rs,2},dp_{ls,2}+dp_{rs,1}) \]

转移代码（复制粘贴大法好！）：

dp[x][1]+=max(dp[lc[x]][2]+dp[rc[x]][3],dp[lc[x]][3]+dp[rc[x]][2]);
dp[x][2]=max(dp[lc[x]][1]+dp[rc[x]][3],dp[lc[x]][3]+dp[rc[x]][1]);
dp[x][3]=max(dp[lc[x]][1]+dp[rc[x]][2],dp[lc[x]][2]+dp[rc[x]][1]);

当然，不要忘了初始化 \(dp_{x,1}\) 为 \(1\)。由于染绿色蓝色红色都是一样的，所以答案就是 \(\max(dp_{x,1},dp_{x,2},dp_{x,3})\) 啦。

求最小值同理，DFS 代码如下（码风一坨）：

void dfs(int x){
	dp[x][1]=dp2[x][1]=1,dp2[x][2]=dp2[x][3]=0;
	if(lc[x]!=0)dfs(lc[x]);
	if(rc[x]!=0)dfs(rc[x]);
	if(lc[x]==0&&rc[x]==0)return;
	dp[x][1]+=max(dp[lc[x]][2]+dp[rc[x]][3],dp[lc[x]][3]+dp[rc[x]][2]);
	dp[x][2]=max(dp[lc[x]][1]+dp[rc[x]][3],dp[lc[x]][3]+dp[rc[x]][1]);
	dp[x][3]=max(dp[lc[x]][1]+dp[rc[x]][2],dp[lc[x]][2]+dp[rc[x]][1]);
	dp2[x][1]+=min(dp2[lc[x]][2]+dp2[rc[x]][3],dp2[lc[x]][3]+dp2[rc[x]][2]);
	dp2[x][2]=min(dp2[lc[x]][1]+dp2[rc[x]][3],dp2[lc[x]][3]+dp2[rc[x]][1]);
	dp2[x][3]=min(dp2[lc[x]][1]+dp2[rc[x]][2],dp2[lc[x]][2]+dp2[rc[x]][1]);
}

值得一提的是，这道题的建树挺特别的，在本文主要讲的是树形DP，所以建树就不多提了，大家可以自行参考题解或者我的代码（绝对不是因为我懒）

3.3.3 代码

代码：

#include<bits/stdc++.h>
using namespace std;
int lc[500010],rc[500010],dp[500010][5],dp2[500010][5],n=1;
int build(int x,int pos){
	char c=getchar();
	if(c=='0')return pos;
	else if(c=='1'){
		lc[x]=++n;
		pos=build(n,pos+1);
	}
	else{
		lc[x]=++n;
		pos=build(n,pos+1)+1;
		rc[x]=++n;
		pos=build(n,pos);
	}
	return pos;
}
void dfs(int x){
	dp[x][1]=dp2[x][1]=1,dp2[x][2]=dp2[x][3]=0;
	if(lc[x]!=0)dfs(lc[x]);
	if(rc[x]!=0)dfs(rc[x]);
	if(lc[x]==0&&rc[x]==0)return;
	dp[x][1]+=max(dp[lc[x]][2]+dp[rc[x]][3],dp[lc[x]][3]+dp[rc[x]][2]);
	dp[x][2]=max(dp[lc[x]][1]+dp[rc[x]][3],dp[lc[x]][3]+dp[rc[x]][1]);
	dp[x][3]=max(dp[lc[x]][1]+dp[rc[x]][2],dp[lc[x]][2]+dp[rc[x]][1]);
	dp2[x][1]+=min(dp2[lc[x]][2]+dp2[rc[x]][3],dp2[lc[x]][3]+dp2[rc[x]][2]);
	dp2[x][2]=min(dp2[lc[x]][1]+dp2[rc[x]][3],dp2[lc[x]][3]+dp2[rc[x]][1]);
	dp2[x][3]=min(dp2[lc[x]][1]+dp2[rc[x]][2],dp2[lc[x]][2]+dp2[rc[x]][1]);
}
signed main(){
	build(1,0);
	dfs(1);
	cout<<max(dp[1][1],max(dp[1][2],dp[1][3]))<<' '<<min(dp2[1][1],min(dp2[1][2],dp2[1][3]))<<endl;
	return 0;
}

4.拓展-树形DP求树的直径

不难发现，一棵树的直径一定是由某一个节点 \(x\) 和两条或一条与 \(x\) 相连的路径所组成的。

所以，树的直径必定在距离每个点 \(x\) 的最长的路径和次长的路径之中，我们可以维护一个数组 \(dp\) 和 \(dp2\)，\(dp_i\) 和 \(dp2_i\) 分别表示距离 \(i\) 最长和次长的路径的长度，经过 \(i\) 的答案就是 \(dp_i+dp2_i\)，最后遍历求 \(\max(dp_i)\) 找答案。

代码很好写，就不推 \(dp\) 和 \(dp2\) 的数组的转移了，代码：

#include<bits/stdc++.h>
using namespace std;
int dp[100010],dp2[100010];
vector<int>v[100010];
void dfs(int x,int fa){
//  dp[x]=dp2[x]=-1e9;如果有负边权就需要初始化，但是叶节点的dp要初始化成0，具体代码看下面。
//  bool flag=false;判断该节点是不是叶节点，如果能向下遍历就不是叶节点
	for(auto i:v[x]){
		if(i==fa)continue;//不能走回头路
//      flag=true;//如果可以继续向下搜索就不是叶节点
		dfs(i,x);//继续搜索
		if(dp[i]+1>dp[x]){//注意这里如果有边权要加上边权
        //如果从这条路走的长度比dp[x]要长
			dp2[x]=dp[x];//更新，把dp[x]传下去给dp2[x]
			dp[x]=dp[i]+1;//更新dp[x]
		}
		else if(dp[i]+1>dp2[x]){
      //如果从这条路走的长度比dp2[x]要长
			dp2[x]=dp[i]+1;//直接更新dp2[x]
		}
	}
//if(!flag)dp[i]=dp2[i]=0;如果是叶节点就要初始化成0
	return;
}
int main(){
	int n,ans=0;//ans用于最后求max，所以如果有负边权就要初始化成-1e9
	cin>>n;
	for(int i=1;i<n;i++){
		int x,y;
		cin>>x>>y;
		v[x].push_back(y);
		v[y].push_back(x);//建图
	}
	dfs(1,-1);//从什么点遍历都可以
	for(int i=1;i<=n;i++){//注意最后要遍历找答案
		ans=max(ans,dp[i]+dp2[i]);//dp[i]+dp2[i]就是经过点i的最长的路
	}
	cout<<ans<<endl;
	return 0;
}

友情客串：万字详解树的直径！

5.作业

P2016 战略游戏难度：\(2/5\)。
P4084 [USACO17DEC] Barn Painting G 难度：\(3/5\)。
P3177 [HAOI2015] 树上染色难度：\(4.5/5\)。

6.闲话

蒟蒻不才，膜拜大佬，如果文章有什么问题，请在评论区@我。

posted @ 2025-06-02 22:49 doooge 阅读(77) 评论(0) 收藏举报

刷新页面返回顶部

doooge

小升初蒟蒻，请大佬多多指教