Codeforces Edu Round 64 A-D
A. Inscribed Figures
分类讨论打表即可。
PS:这道题翻译有歧义。
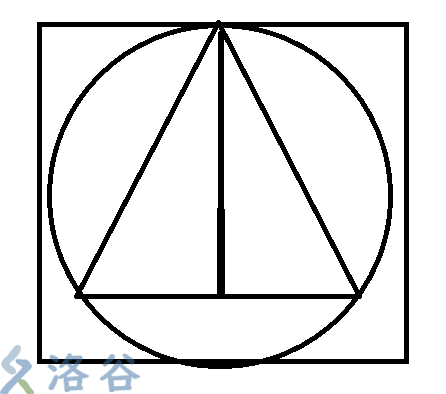
这样稍微翻转一下,就可以是\(7\)个交点呀...(大概是我没看英文题干导致的惨案)
#include <cstdio>
#include <iostream>
using namespace std;
const int N = 110;
int n, a[N], ans = 0;
int d[3][3]{
{-1, 3, 4},
{3, -1, -1},
{4, -1, -1}
};
int main(){
scanf("%d", &n);
for(int i = 1; i <= n; i++)
scanf("%d", a + i);
for(int i = 2; i <= n; i++){
int res = d[a[i - 1] - 1][a[i] - 1];
if(i > 1 && i + 1 <= n && a[i + 1] == 2 && a[i] == 1 && a[i - 1] == 3) res = 3;
if(res == -1){
puts("Infinite");
return 0;
}else{
ans += res;
}
}
printf("Finite\n%d\n", ans);
return 0;
}
B. Ugly Pairs
将奇数字母\((char - 'a') \& 1\)与偶数字母分别分开来升序排序,设为\(A\)、\(B\)。
尝试\(AB\)或者\(BA\),若都不行则无解(注意,题有坑,\(za\)是可以的,而\(az\)不行)
证明:
\(A\)与\(B\)都满足\(str[i] <= str[i + 1] (1 <= i < len)\)
若\(A.end()\)不满足\(B.begin()\),反过来匹配也不行。则说明无论怎么拼,它们都是不严谨递增的。
则它们的开头与结尾是相邻的,它们相当于一个并行的状态,必须有一方是不严谨递增的重复字母且一方邻向。(否则不可能不严谨递增)
#include <cstdio>
#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110;
char s[N];
int n, vis[N];
vector<char> A, B;
char inline pre(char c){
return 'a' + ((c - 'a' + 25) % 26);
}
char inline nxt(char c){
if(c == 'z') return '?';
return 'a' + ((c - 'a' + 1) % 26);
}
int main(){
int T; scanf("%d", &T);
while(T--){
A.clear(); B.clear();
scanf("%s", s + 1);
n = strlen(s + 1);
for(int i = 1; i <= n; i++){
if((s[i] - 'a') & 1) A.push_back(s[i]);
else B.push_back(s[i]);
}
sort(A.begin(), A.end());
sort(B.begin(), B.end());
if(A.empty() || B.empty()){
for(int i = 0; i < A.size(); i++)
putchar(A[i]);
for(int i = 0; i < B.size(); i++)
putchar(B[i]);
printf("\n");
}else if(pre(A.back()) != B[0] && nxt(A.back()) != B[0]){
for(int i = 0; i < A.size(); i++)
putchar(A[i]);
for(int i = 0; i < B.size(); i++)
putchar(B[i]);
printf("\n");
}else if(pre(B.back()) != A[0] && nxt(B.back()) != A[0]){
for(int i = 0; i < B.size(); i++)
putchar(B[i]);
for(int i = 0; i < A.size(); i++)
putchar(A[i]);
printf("\n");
}else puts("No answer");
}
return 0;
}
C. Match Points
发现答案具有单调性,既然有\(3\)个,那么一定有\(2\)对,可以二分答案。
\(check()\)函数的检查是一个贪心的过程,使\(x_i\)匹配\(x_{(n / 2) + i}\)这样是很明显最优的方案。
证明:
存在\(x_a <= x_b <= x_c <= x_d\)
若\((a, b),(c, d)\) 可匹配成功,那么\((a, c),(b, d)\)必定能匹配成功,反命题则不然。
那么\(x_b - x_a >= z\),也就是\(x_c >= x_b >= z + x_a\),换过来就是\(x_c - x_a >= z\)
\((b, d)\)的证明同理,所以一一匹配一定是最优的。
PS:写完了程序才发现可以直接\(O(n)\)求解,看了题解才知道自己太弱了...
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 200010;
int n, z, x[N];
bool check(int m){
for(int i = 1; i <= m; i++)
if(x[n - m + i] - x[i] < z) return false;
return true;
}
int main(){
scanf("%d%d", &n, &z);
for(int i = 1; i <= n; i++)
scanf("%d", x + i);
sort(x + 1, x + 1 + n);
int l = 0, r = n / 2;
while(l < r){
int mid = (l + r + 1) >> 1;
if(check(mid)) l = mid;
else r = mid - 1;
}
printf("%d\n", l);
return 0;
}
D. 0-1-Tree
自闭,想不到什么好方法,\(dp\)死活想不出来...
计数问题,可以利用加法原理分开处理。
符合条件的点对\((u, v)\)有三种情况:
- 全部是\(0\)边
- 全部是\(1\)边
- 先经过一些\(0\)边,然后经过\(1\)边
对于情况\(1\),我们可以考虑让图仅存在\(0\)边,然后对于每个连通块,它的点对数量为:
\(size * (size - 1)\)。可以理解为每一个点可以找另外连通块的所有点,交换下来仍然成立。
对于情况\(2\),同理情况\(2\)。
对于情况\(3\),可以考虑找到一个截点\(x\),路径考虑为\(s -> x -> t\),\(s - > x\)上的路径全部为\(0\),\(x -> t\)的路径全部为\(1\)。这种情况,方案数为\((size_{x属于的0边连通块} - 1) * (size_{x属于的1边连通块} - 1)\),理解为在\(x\)属于的\(0\)边连通块中找一个点\(s(s != x)\) ,在\(1\)边同理。
对于上述所有操作,仅仅是集合之间的合并,可以用并查集维护。
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long LL;
const int N = 200010, M = N << 1;
int n, f[N][2], size[N][2];
LL ans = 0;
int inline find(int x, int c){
return f[x][c] == x ? x : f[x][c] = find(f[x][c], c);
}
void merge(int a, int b, int c){
a = find(a, c), b = find(b, c);
if(a != b) f[a][c] = b, size[b][c] += size[a][c];
}
int main(){
scanf("%d", &n);
for(int i = 1; i <= n; i++){
f[i][0] = f[i][1] = i;
size[i][0] = size[i][1] = 1;
}
for(int i = 1, u, v, w; i < n; i++){
scanf("%d%d%d", &u, &v, &w);
merge(u, v, w);
}
for(int i = 1; i <= n; i++){
if(f[i][0] == i)
ans += (LL)size[i][0] * (size[i][0] - 1);
if(f[i][1] == i)
ans += (LL)size[i][1] * (size[i][1] - 1);
int p = find(i, 0), q = find(i, 1);
ans += (LL)(size[p][0] - 1) * (size[q][1] - 1);
}
printf("%lld\n", ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号