模式识别第三次作业

第三次作业

6.3

(a) 由于2范数\(\| A\|_2=\sigma_{max}\)（又叫谱范数），其中\(\sigma_{max}\)为\(A\)的最大奇异值，故

\[\kappa(X)=\sigma_{max}*\frac{1}{\sigma_{min}}=\frac{\sigma_1}{\sigma_n} \]

(b) 假设存在一个小的扰动\(\varDelta x\)导致一个\(\varDelta y\)，即

\[A(x+\varDelta x)=b+\varDelta b \]

则\(\varDelta x = A^{-1}\varDelta b\)，两边取二范数：\(\|\varDelta x\|\leq \| A^{-1} \| \| \varDelta b \|\)

由根据\(Ax=b\)，有\(\| b \|\leq \| A\| \|x\|\)

根据以上两式有：

\[\frac{\varDelta x}{x}\leq(\|A\|\|A^{-1}\|)\frac{\|\varDelta b\|}{\|b\|}=\kappa_2(A)\frac{\|\varDelta b\|}{\|b\|} \]

由上式可知，当存在扰动量时，解的相对误差与矩阵的条件数成正比，即较小的\(\varDelta x​\)会造成较大的\(\varDelta y​\)，因此\(\kappa_2(A)​\)很大时，线性系统是病态的。

(c) 证明：对于正交矩阵\(A\)，\(A^TA=AA^T=1\),

则\(\|A\|_2=\sqrt{\rho(A^TA)}=1\)，\(\|A^{-1}\|_2=\sqrt{\rho(AA^T)}=1\)，故：

\(\kappa_2(A)=\|A\|_2\|A_{-1}\|_2=1\)

由第一题知，矩阵条件数\(\frac{\sigma_1}{\sigma_n}\)不会比1小，且正交矩阵的条件数为1，因此正交矩阵是良态的。

6.6

(c) 环境 ubuntu16.04 OPenCv2.4 C++ cmake文件：

project(face_recognition)
set( CMAKE_CXX_FLAGS "-std=c++11" )
set( OpenCV_FOUND 1 )
find_package(OpenCV 2.4 REQUIRED PATHS "/home/dlutjwh/opencv-2.4")
include_directories( ${OpenCV_INCLUDE_DIRS} )
add_executable(fisherface facerec_fisherfaces.cpp)
add_executable(eigenface facerec_eigenfaces.cpp)
target_link_libraries( fisherface ${OpenCV_LIBS} )
target_link_libraries( eigenface ${OpenCV_LIBS} )

Eigenface实验结果：

前面十个为eigenfaces，后面为每隔15个特征向量进行重建后的效果图，最后一张图为平均脸。

FisherFace实验结果：

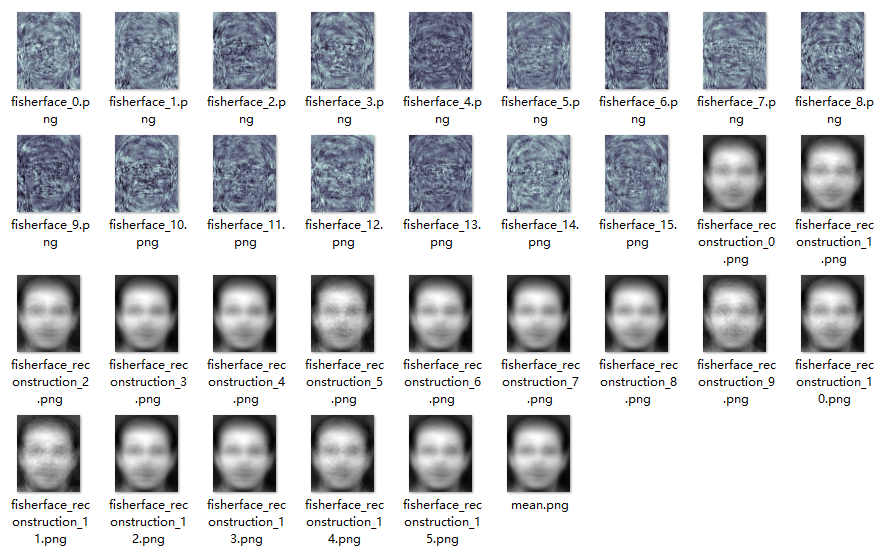
前面16张为fisherface，后面为重建效果，最后一张为平均脸。

总结：从效果上来看，fisherface似乎难以重建出原图像，可能由于FisherFace只关注各类目标间的不同特征，难以复原图像。而PCV没有考虑label，降维后可能失去了类和类之间的区别信息。

(d)

最右边为原图像，大概需要225-230张左右，重构图像与原图像难以区分。

7.1

(a) 阅读软件包并编译成功，实验环境：ubuntu16.04，在Makefile所在文件夹下进行make操作

(b)

1. 默认参数下，命令：./svm-train svmguide1（训练） ./svm-predict svmguide1.t svmguide1.model svmguide1.t.predict （测试） 准确率： Accuracy = 66.925% (2677/4000) 以第一题为例截图如下：


2. 特征规范化到\([-1,1]\)区间，命令：
   ./svm-scale -l -1 -u 1 -s range1 svmguide1 > svmguide1.scale （缩放）
   ./svm-scale -r range1 svmguide1.t > svmguide1.t.scale （测试集同样进行缩放）
   ./svm-train svmguide1.scale （训练）
   ./svm-predict svmguide1.t.scale svmguide1.scale.model svmguide1.t.predict （测试） 准确率：Accuracy = 96.15% (3846/4000)

3. 采用线性核，命令：
   ./svm-train -t 0 svmguide1 （训练）
   ./svm-predict svmguide1.t svmguide1.model svmguide1.t.predict （测试） 准确率：Accuracy = 95.675% (3827/4000)

4. \(C=1000\)，以RBF核，命令：
   ./svm-train -c 1000 svmguide1 （训练）
   ./svm-predict svmguide1.t svmguide1.model svmguide1.t.predict （测试）
   准确率：Accuracy = 70.475% (2819/4000)

5. 确定超参数：


​ \(C=2.0, \gamma=2.0\)

​ 总结：在使用学习算法之前进行特征规范化很有必要，归一化后效果好很多。如果模型不是很复杂，使用RBF核可能会带来过拟合的问题，效果反而不好。另外适当增大参数\(C\)的大小可以提高准确率。

(c) 使用原网站a6a数据集，训练集中标签有两个，-1和1，其中-1的占比较大，采用-wi参数：
命令： ./svm-train -w-1 1 -w1 1.5 a6a 其中权值比重为1:1.5，准确率由 84.1713% (17963/21341)上升到84.5321% (18040/21341)，考虑到测试集较大，准确率还是有一定提高。

8.2

(a) 证明:

\[\int_{x_m}^{\infty}p_1(x)dx=\int_{x_m}^{\infty}\frac{c_1}{x^{\alpha+1}}dx=\frac{c_1}{\alpha x_m ^\alpha}=1 \]

解得：\(c_1=\alpha x_m^\alpha\)，故\(p_1(x)=p(x)\)，X服从pareto(\(x_m,\alpha\)).

(b)似然函数：

\[p(D|x_m,\alpha)=\Pi_{i=1}^{n}p(x_i|x_m,\alpha)=\Pi_{i=1}^{n}\frac{\alpha x_m^\alpha}{x^{\alpha+1}}[x\geq x_m] \]

易知该函数为\(x_m\)的非减函数，故\(x_{min}\)的估计值为\(\min \left\{ x_i,1\leq i\leq n \right \}\)，进而：

\[p(D|x_{m},\alpha)=\frac{\alpha^nx_{min}^{\alpha n}}{\Pi_{i=1}^{n} x_i^{\alpha+1}} \]

取对数后对\(\alpha\)求导：

\[\frac{\partial\ln P}{\partial \alpha}=\frac{\partial (n\ln\alpha +n\alpha \ln x_{min}-(\alpha+1)\ln x_i)}{\partial \alpha}={\frac{n}{\alpha}+n\ln x_{min}-\sum_{i=1}^{n}\ln x_i} \]

令其等于0解得:

\[\alpha = \frac{n}{\sum_{i=1}^{n}x_i-n\ln x_{min}}\ \ , x_m=\min \left\{ x_i,1\leq i\leq n \right \} \]

(3)

\[p(\theta|D)=m \Pi_{i=1}^{n}p(x_i|\theta)p(\theta)=m\Pi_{i=1}^{n}\frac{1}{\theta}\frac{k x_m^k}{\theta^{k+1}}=m\frac{k^nx_m^{k n}}{\theta^{n(k+2)}} \]

PDF积分后归一化：

\[\int_{x_m}^{\infty}p(\theta|D)d\theta=m\int_{x_m}^{\infty}\frac{k^nx_m^{k n}}{\theta^{n(k+2)}}d\theta=m\frac{k^nx^{-2n+1}}{k n+2n-1}=1 \]

解得：

\[m=\frac{k n+2n-1}{k^nx_m^{-2n+1}} \]

带回去：

\[p(\theta|D)=\frac{(k n+2n-1)x_m^{k n+2n-1}}{\theta^{(k+2)n}} \]

故后验也是一个Pareto(\(x_m,kn+2n-1\))分布。

9.6

(a) 阅读软件包并编译成功，实验环境：ubuntu16.04，在Makefile所在文件夹下进行make操作

(b) 默认参数命令：/train mnist （训练） ./predict mnist.t mnist.model mnist.t.predict（测试）

准确率：Accuracy = 80.26% (8026/10000)

(c) 训练和测试命令不变，train.c中修改代码：x_space[j].value = sqrt(x_space[j].value); predict.c中修改代码：x[i].value=sqrt(x[i].value); 准确率：Accuracy = 87.22% (8722/10000)

(d) 由上述实验，开根变换后准确率有所上升。由于mnist数据集的特征取值范围大约在0-300左右，跨度较大，且某些特征的取值范围比其他特征大得多，特征值较大的特征影响占比太大，进行开根变换后特征值的相对大小没有改变，但是总体缩小了，因此取值较大的特征值对结果影响降低，使得准确率上升。

10.2

(a) 对于两个向量\(\boldsymbol x\)，\(\boldsymbol y\)，\(\boldsymbol z\)距离度量\(d\)需要满足非负性：\(d(\boldsymbol x,\boldsymbol y)\geq0\)，对称性：\(d(\boldsymbol x,\boldsymbol y)=d(\boldsymbol y,\boldsymbol x)\)，同一性\(d(\boldsymbol x,\boldsymbol y)=0 <=> \boldsymbol x = \boldsymbol y\)，三角不等式\(d(\boldsymbol x,\boldsymbol z)\leq d(\boldsymbol x,\boldsymbol y)+d(\boldsymbol y,\boldsymbol z)\)

(b)根据公式\(KL(p\|q)=\sum_xp(x)\log_2\frac{p(x)}{q(x)}\)

\[\begin{split} KL(A\|B)&=\frac{1}{2}\log_2\frac{\frac{1}{2}}{\frac{1}{4}}+\frac{1}{2}\log_2\frac{{\frac{1}{2}}}{\frac{3}{4}}=1-\frac{1}{2}\log_23\\ KL(B\|A)&=\frac{1}{4}\log_2\frac{\frac{1}{4}}{\frac{1}{2}}+\frac{3}{4}\log_2\frac{{\frac{3}{4}}}{\frac{1}{2}}=\frac{3}{4}\log_23-1\\ KL(A\|C)&=\frac{1}{2}\log_2\frac{\frac{1}{2}}{\frac{1}{8}}+\frac{1}{2}\log_2\frac{{\frac{1}{2}}}{\frac{7}{8}}=2-\frac{1}{2}\log_27\\ KL(C\|A)&=\frac{1}{8}\log_2\frac{\frac{1}{8}}{\frac{1}{2}}+\frac{7}{8}\log_2\frac{{\frac{7}{8}}}{\frac{1}{2}}=\frac{7}{8}\log_27-2\\ KL(B\|C)&=\frac{1}{4}\log_2\frac{\frac{1}{4}}{\frac{1}{8}}+\frac{3}{4}\log_2\frac{{\frac{3}{4}}}{\frac{7}{8}}=\frac{3}{4}\log_26-\frac{3}{4}\log_27-\frac{1}{4}\\ KL(C\|B)&=\frac{1}{8}\log_2\frac{\frac{1}{8}}{\frac{1}{4}}+\frac{7}{8}\log_2\frac{{\frac{7}{8}}}{\frac{3}{4}}=\frac{7}{8}\log_27-\frac{7}{8}\log_26-\frac{1}{8}\\ \end{split} \]

上述各式均不小于0，故满足非负性，\(KL(A\|B)\neq KL(B\|A)\)，故不满足对称性，\(KL(A,A)=0\)，\(A,B,C\)满足同一性。\(KL(A\|C)>KL(A\|B)+KL(B\|C)\)，故不满足三角不等式。

(c) matlab中检验：

DisAB = A(1)*log2(A(1)/B(1))+A(2)*log2(A(2)/B(2))
DisBA = B(1)*log2(B(1)/A(1))+B(2)*log2(B(2)/A(2))
DisAC = A(1)*log2(A(1)/C(1))+A(2)*log2(A(2)/C(2))
DisCA = C(1)*log2(C(1)/A(1))+C(2)*log2(C(2)/A(2))
DisCB = C(1)*log2(C(1)/B(1))+C(2)*log2(C(2)/B(2))
DisBC = B(1)*log2(B(1)/C(1))+B(2)*log2(B(2)/C(2))
DisAC-(DisAB+DisBC)>0  输出1
DisAB =  0.20752;DisBA =  0.18872;DisAC =  0.59632;
DisCA =  0.45644;DisCB =  0.069593;DisBC =  0.083206;

10.6

根据已知设熵为\(h(x)\)：

\[\begin{split} &h(x)=-\int_0^{\infty} q(x)\ln q(x) dx\\ &\max h(x),st.\ \int_0^\infty q(x)dx=1,q(x)\geq 0,\int_0^\infty xq(x)dx=\mu \end{split} \]

使用拉格朗日乘子法：

\[\begin{split} L(q,a,b,c)=-\int_0^{\infty} q(x)\ln q(x) dx+a(\int_0^\infty q(x)dx-1)+bq(x)+c(\int_0^\infty xq(x)dx-\mu) \end{split} \]

对\(q\)求导并令其等于0：

\[\frac{\partial L}{\partial q}=-\ln q(x)+1+a+b+cx=0 \]

解得：

\[q(x)=e^{-cx-a-b-1}=me^{-nx} \]

根据已知：

\[\int_0^{\infty}q(x)dx=\frac{m}{n}=1 => \ \ m=n\\ \int_0^{\infty}xq(x)dx=\int_0^{\infty} mxe^{-mx}dx=\frac{1}{m}=u\ \ => \ \ m=\frac{1}{\mu} \]

故参数为\(\frac{1}{\mu}\)的实数分布是这样约束条件的最大熵分布。