pytorch神经网络-一个简单例子的分解

import torch
import torch.nn as nn
import torch.optim as optim

# 定义神经网络
class SimpleNN(nn.Module):　　
 '''　　

　　fc1 的输出维度是 128，这个张量直接作为 fc2 的输入，因此需要让 fc2 的 in_features 也等于 128。这个数值是人为设计的，确保层与层之间的张量尺寸匹配。



　　若 fc1 输出 256，就必须将 fc2 的输入改为 256，否则张量形状不匹配会报错。

 '''
def __init__(self):
        super(SimpleNN, self).__init__()
        # 定义一个输入层到隐藏层的全连接层
        self.fc1 = nn.Linear(28 * 28, 128)  # 输入层到隐藏层----输入 28×28 像素（例如 MNIST 手写数字）的输入，这里把展平后的 784 维像素映射到 128 维隐藏表示
        # 定义一个隐藏层到输出层的全连接层
        self.fc2 = nn.Linear(128, 10)       # 把 128 维隐藏表示映射到 10 维输出（对应 10 个类别）。

    def forward(self, x):
        # 前向传播过程
        x = x.view(-1, 28 * 28)  # 展平输入
        x = torch.relu(self.fc1(x))  # 激活函数ReLU，常用于隐藏层。
        x = self.fc2(x)    # 输出层
        return x

# 创建模型实例
model = SimpleNN()

# 定义损失函数和优化器
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

# 示例输入
input = torch.randn(1, 28, 28)  # 随机生成一个28x28的输入
output = model(input)  # 前向传播
loss = criterion(output, torch.tensor([3]))  # 假设真实标签为3

# 反向传播和优化
optimizer.zero_grad()
loss.backward()
optimizer.step()

print("输出：", output)
print("损失：", loss.item())

整体意义：

演示了典型的 PyTorch 训练步骤——定义损失与优化器，构造输入并前向传递，计算损失，清空梯度、反向传播，再由优化器执行参数更新。

基础概念：

在进行模型训练时，有三个基础的概念：

　　1. Epoch: 使用全部数据对模型进行以此完整训练，训练轮次

　　2. Batch_size: 使用训练集中的小部分样本对模型权重进行以此反向传播的参数更新，每次训练每批次样本数量

　　3. Iteration: 使用一个 Batch 数据对模型进行一次参数更新的过程

假设数据集有 50000 个训练样本，现在选择 Batch Size = 256 对模型进行训练。

每个 Epoch 要训练的图片数量：50000

训练集具有的 Batch 个数：50000/256+1=196

每个 Epoch 具有的 Iteration 个数：196

10个 Epoch 具有的 Iteration 个数：1960

batch_size：一次前向/反向传入网络的样本数量。比如一次喂 32 张图片，就叫 batch_size=32。PyTorch 张量的第一维通常就是 batch 维，用来同时处理多张图

梯度：

　　是“损失对每个参数的偏导数”，表示“参数微小变化时，损失会如何变化”。

正梯度：参数增大，损失增大（应减小参数）

负梯度：参数增大，损失减小（应增大参数）

梯度绝对值：影响强度

例如，fc1.weight 的某个梯度是 -0.5，表示该权重增加 1，损失大约减少 0.5。

交叉熵是什么

交叉熵是信息论中衡量两个概率分布差异性的核心指标，在机器学习中常被用作分类模型的损失函数。其本质是通过量化真实分布与预测分布之间的信息差异，指导模型优化方向。

定义与核心思想

交叉熵公式为

关键特性

非对称性：交叉熵不具备对称性，
灵敏度优势：对预测概率的微小偏差敏感，当真实类别预测概率从0.9降低到0.8时，交叉熵损失的增长幅度远大于均方误差
数学优化友好：作为凸函数具有唯一极值点，配合Softmax激活函数时梯度计算简洁，便于反向传播

代码解释：

criterion = nn.CrossEntropyLoss()

　　定义损失函数和优化器-----创建交叉熵损失，是分类任务最常用的目标函数，内部会对模型输出做 log_softmax 并与真实标签对齐，对应“希望模型对正确类别给出最高对数概率”的目标。

　　通俗来讲：这句话在“定规则”：告诉模型，分类任务要用“交叉熵”衡量对错。

　　　　　　　交叉熵可以理解成：如果模型说“3”最可能，而真实答案确实是 3，损失就小；答错损失就大。

optim模块

　　优化器主要用在模型训练阶段，用于更新模型中可学习的参数。优化器主要用在模型训练阶段，用于更新模型中可学习的参数。torch.optim提供了多种优化器接口，比如Adam、RAdam、SGD、ASGD、LBFGS等，Optimizer是所有这些优化器的父类。

　　optim模块是用于实现各种优化算法的核心组件，支持SGD、Adam等主流优化器，并提供参数分组、状态管理等功能。

核心公共方法说明：

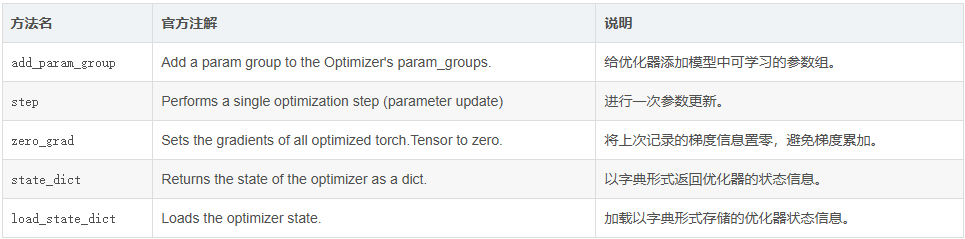
　　Optimizer的init函数接收两个参数：一个是需要被优化的参数，其形式必须是Tensor或者dict；另一个是优化选项，包括学习率、衰减率等。第一个位置通常是model.parameters()填充，如有其他要求，也可手动写一个dict作为输入。仅需要保证dict中存在['params']键即可，其他键可以按照自己的要求填写。

optimizer = optim.SGD(model.parameters(), lr=0.01)

　　相当于给模型配了一个“学习方法”。SGD 就是最传统的“梯度下降”算法，lr=0.01 是学习率，决定每次更新走多远。

第二个参数学习率（lr）是不是设置越大越好？为什么？

　　不是。学习率过大或过小都有问题。

学习率过小（如 0.0001）：更新步长太小，收敛慢，可能卡在局部最优

学习率过大（如 10）：更新步长太大，可能跳过最优解，导致损失震荡甚至发散

　　经验值：

常用范围：0.001 到 0.1

你的代码用 0.01 是合理的起点

实际训练中可能需要根据效果调整

input = torch.randn(1, 28, 28)

　　准备一张“假图片”当训练样本，用随机数生成形状 1×28×28（1 张 28×28 图像）。

　　这里只是为了演示流程，不是真正的手写数字。

　　其中，input = torch.randn(1, 28, 28) 这一行生成的张量本身就是形状 [batch_size, 28, 28]，其含义是“batch_size 张、每张 28×28 像素的灰度图”。在上面的例子里 batch_size=1，所以张量形状就是 [1, 28, 28]；如果一次喂 32 张图片，就会是 [32, 28, 28]。view(-1, 28 * 28) 只是把这种“批次维 + 图像行列”结构拉直为 [batch_size, 784] 的二维矩阵：第一维仍然是批次里的样本数，第二维把 28×28 的像素顺序地排列成长度 784 的一维向量。之所以需要这么做，是因为 nn.Linear(28 * 28, 128) 要求每个输入样本是一个 784 维向量，如果不展开就无法接到全连接层上。

output = model(input)

把假图输入模型，得到一个长度为 10 （执行了model的init和forword，输出为10）的输出向量（logits），每个数字代表“模型认为某个类别的得分”。

loss = criterion(output, torch.tensor([3]))

计算了损失值：假设真实标签为3----以“真实标签 3”计算交叉熵损失，衡量模型输出与期望答案之间的误差。

用之前设定的交叉熵规则计算“模型输出”与“真实标签”的差距，得到一个数字 loss。

optimizer.zero_grad()

在正式算梯度前，先把上一次的梯度清零，避免不同批次之间互相影响。

为什么正式算梯度前要上一次梯度清零？当前代码在这之前有算梯度吗？

原因：PyTorch 默认会累积梯度。如果不清零，新计算的梯度会累加到旧的梯度上，导致更新错误。

# 第一次迭代
loss1.backward()  # 梯度 = 0.5
optimizer.step()  # 更新参数

# 第二次迭代（如果没有zero_grad）
loss2.backward()  # 梯度 = 0.3，但会累加到0.5上，变成0.8！
optimizer.step()  # 用错误的梯度0.8更新，而不是0.3

当前代码在这之前有算梯度吗？在当前代码中，第71行之前没有计算过梯度。这是第一次训练迭代，但 zero_grad() 仍然必要，因为：

模型初始化时，参数的 .grad 可能是 None 或包含随机值

养成习惯：每次迭代前都清零，避免在循环训练时出错

代码可复用：如果这段代码放在循环里，不清零会导致梯度累积

最佳实践：每次 backward() 前都调用 zero_grad()，形成固定模式：

loss.backward()

关键一步：PyTorch 自动计算“损失对每个参数的偏导数”。

loss.backward() 会计算 loss 对 model 中所有参数的梯度（fc1 和 fc2 的权重和偏置）

直观理解：告诉你“每个参数应该往哪个方向调一点，才能让损失变小”。

backward() 是求导函数，使用链式法则自动计算梯度。

针对谁：针对损失函数 loss 对模型所有可训练参数的导数

怎么求：从 loss 开始，沿着计算图反向传播，逐层计算偏导数

loss (标量)
  ↓ backward()
  ↓ 链式法则
  ↓
fc2的权重和偏置的梯度 (∂loss/∂fc2_weight, ∂loss/∂fc2_bias)
  ↓
fc1的权重和偏置的梯度 (∂loss/∂fc1_weight, ∂loss/∂fc1_bias)

当前代码：

optimizer.step()

让优化器根据刚计算出的梯度，结合SGD 规则的学习率，去真正改动参数，完成一次训练迭代。

完成一次“学到经验”的更新，理论上模型会稍微更擅长识别“3”。

因此：

每次循环就包含“前向算输出 → 算损失 → 反向求梯度 → 更新参数”四步。代码片段只是手动写了单次循环的全过程，帮助你理解 PyTorch 基本训练逻辑。

再次解释：四步分别对应哪行代码？

# 第一步：前向算输出
output = model(input)  # 第67行

# 第二步：算损失
loss = criterion(output, torch.tensor([3]))  # 第68行

# 第三步：反向求梯度
loss.backward()  # 第72行

# 第四步：更新参数
optimizer.step()  # 第73行

posted @ 2025-11-26 15:25 c++c鸟阅读(37) 评论(0) 收藏举报

刷新页面返回顶部

c++,c随笔