图论

几个笔记无脑合并的，有亿点乱，而且未完成

图论概述

图

图结构是描述和解决实际应用问题的一种基本而有力的工具 ——《数据结构》

图的定义：所谓的图可定义为 \(G = (V, E)\) ，其中集合 \(V\) 中的元素叫做 节点(node)，集合 \(E\) 中的元素叫做 边(edge)。每条边对应 \(V\) 集合中的一对节点 \((u, v)\) ，代表他们有一定的关系。

为了方便计算，\(V\) 和 \(E\) 都是有限集。

无向图、有向图以及混合图

可大致按照边有无方向将图分为无向图和有向图。

对于边集 \(E\) 中的元素 \((u, v)\)，如果 \(u\) 和 \(v\) 的次序无所谓，则这样的图称为有向图，否则称为无向图，有时一张图中两者皆有，称为混合图。

其实不用考虑那么多，可以对于无向边双向建边，这样可以都转化为有向图。

度

对于一张图的每个节点，与其关联的边数称为度。

对于一条有向边 \((u, v)\) ，对于节点 \(u\) 的出度有 1 贡献，对于 \(v\) 的入度有 1 贡献。

简单图

简单图即为没有自环的图。自环即为两端连接同一节点的边。这类边可能确实有其独特意义，如在城市交通图中，但是一般不讨论自环，有一些题目的数据会出现自环，但这可能是数据随机生成的缘故，对于题目没什么影响，除非觉得存不下特判一下。

通路与回路

所谓通路，也就是路径，是 \(m + 1\) 个节点和 \(m\) 条边交替组成的序列。

\(\pi = \{v_0, e_1, v_1, e_2 ...v_m\}\)

对于任何 \(0 < i \le m\) ，\(e_i = (v_{i-1},v_i)\)，也就是说序列中的节点依次首尾相连，其中沿途经过边的数量是 \(m\) ，记 \(|\pi| = m\)。

也可以简化描述，只列出节点：

\(\pi = \{v_0,v_1,v_2...v_m\}\)。

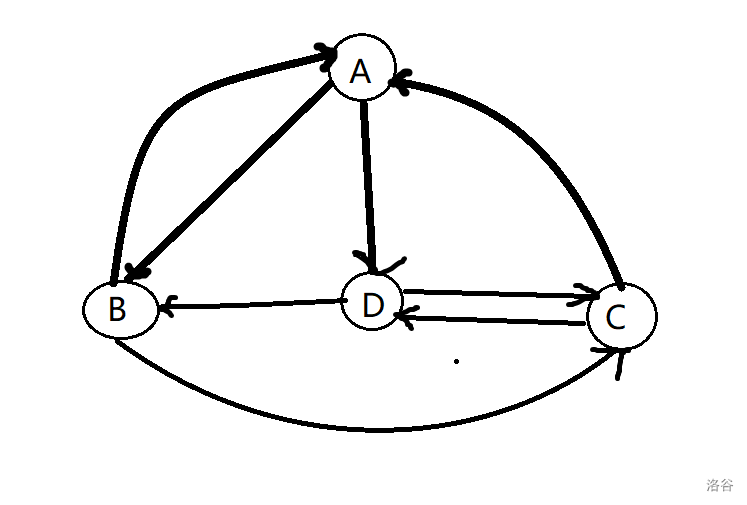
如上图，我们发现，尽管经过的边互不相同，但是经过的节点却可能有重复的。我们将沿途经过节点互异的通路称为简单通路，如下图。

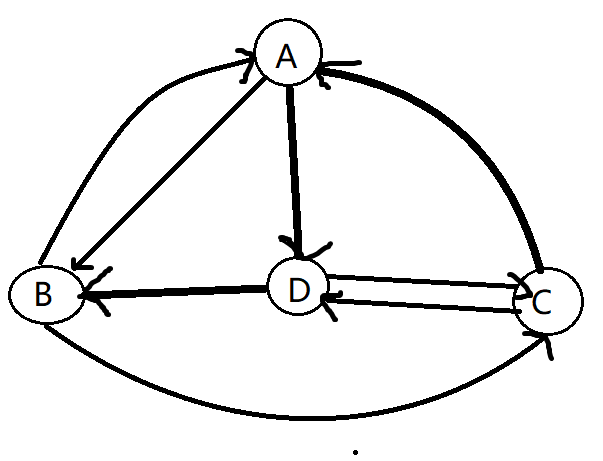
如果一条通路的起始节点和结束节点为同一个，则称为回路，其中，经过每条边恰好一次的回路称为欧拉回路

最小生成树

概念

生成树：即在一个无向连通图中选几条边，使得这个这张图联通；

最小生成树 ： 我们定义无向连通图的 最小生成树（Minimum Spanning Tree，MST）为边权和最小的生成树。

只有连通图才有生成树，对于不连通的图，只有生成生成森林。

Kruskal 算法

实现

Kruskal 算法的基本思想就是：对于一张图，按照边权的从小到大加入边，最后使得这张图连通。

Kruskal 算法的本质其实就是贪心策略，主要贪得是一下两方面：

1. 将边权从小到大排序，先加入边权小的，一定不比先加入边权大的所生成的生成树大；
2. 如果两个节点已经连通，那么不去加入连通这两个点的边一定比加入这个边所形成的生成树小；

基本实现过程如图：

（图寄了）

代码

例题：P3366 【模板】最小生成树

#include<bits/stdc++.h>
#define maxn 200005
using namespace std;
int n, m, as;
int f[maxn];
struct node{
	int u, v, w;
}a[maxn];
bool cmp(node x, node y){
	return x.w < y.w;
}
int find(int k){
    if(f[k]==k)return k;
    return f[k]=find(f[k]);
}
int main(){
	int tot = 0;
	cin >> n >> m;
	for(int i = 1; i <= n; i++) f[i] = i;
	for(int i = 1, u, v, w; i <= m; i++){
		cin >> u >> v >> w;
		a[i].u = u, a[i].v = v, a[i].w = w;
	}
	sort(a+1, a + m + 1, cmp);
	for(int i = 1; i <= m; i++){
		if(find(a[i].u) == find(a[i].v)) continue;
		as += a[i].w;
		f[find(a[i].v)] = find(a[i].u);
		if(++tot == n-1) break;
	}
	if(tot != n-1){
		cout << "orz";
		return 0;
	}
	cout << as;
}

证明（摘自OI.WIKI)

思路很简单，为了造出一棵最小生成树，我们从最小边权的边开始，按边权从小到大依次加入，如果某次加边产生了环，就扔掉这条边，直到加入了 条边，即形成了一棵树。

证明：使用归纳法，证明任何时候 K 算法选择的边集都被某棵 MST 所包含。

基础：对于算法刚开始时，显然成立（最小生成树存在）。

归纳：假设某时刻成立，当前边集为 \(F\)，令 \(T\) 为这棵 MST，考虑下一条加入的边 \(e\)。

如果 \(e\) 属于 \(T\)，那么成立。

否则，\(T + e\) 一定存在一个环，考虑这个环上不属于 \(F\) 的另一条边 \(f\)（一定只有一条）。

首先，\(f\) 的权值一定不会比 \(e\) 小，不然 \(f\) 会在 \(e\) 之前被选取。

然后， \(f\) 的权值一定不会比 \(e\) 大，不然 就是一棵比 \(T\) 还优的生成树了。

所以，\(T + e - f\) 包含了 \(F\) ，并且也是一棵最小生成树，归纳成立。

Prim 算法

实现

Prim 算法的基本思想是从一个结点开始，不断加点（而不是 Kruskal 算法的加边）。

具体来说，每次要选择距离最小的一个结点，以及用新的边更新其他结点的距离。

有一个观察：对应于每个店，其出边边权最小的那个边一定在最小生成树里面。

其实跟 Dijkstra 算法一样，每次找到距离最小的一个点，可以暴力找也可以用堆维护。

堆优化的方式类似 Dijkstra 的堆优化，但如果使用二叉堆等不支持 \(O(1)\) decrease-key 的堆，复杂度就不优于 Kruskal，常数也比 Kruskal 大。所以，一般情况下都使用 Kruskal 算法，在稠密图尤其是完全图上，暴力 Prim 的复杂度比 Kruskal 优，但 不一定 实际跑得更快。

（图寄了）

代码

#include<bits/stdc++.h>
using namespace std;
int n, m, vis[10000];
struct edge {
	int v, w, nxt;
}e[2000005];
int head[200005], cnt;
void add(int u, v, w) {
	e[++cnt].v = v, e[cnt].w = w;
    e[cnt].nxt = head[u], head[u] = 
}
int prim(int x) {
	priority_queue<pair<int, int> > q;
	for (int i = elast[x]; ~i; i = e[i].next) {
		int j = e[i].v;
		q.push({ -e[i].w,j });
	}
	vis[x] = 1;
	int ans = 0, cntt = 0;
	while (q.size()) {
		pair<int, int> temp = q.top();
		q.pop();
		int node = temp.second, value = -temp.first;
		if (vis[node]) continue;
		ans += value, cntt++, vis[node] = 1;
		for (int i = elast[node]; ~i; i = e[i].next) {
			int j = e[i].v;
			if (!vis[j]) {
				q.push({ -e[i].w,j });
			}
		}
	}
	if (cntt != n - 1) return -1;
	return ans;
}
int main() {
	cin >> n >> m;
	memset(elast, -1, sizeof(elast));
	for (int i = 0; i < m; i++) {
		int x, y, z;
		cin >> x >> y >> z;
		add(x, y, z);
		add(y, x, z);
	}
	int t = prim(1);
	if (t == -1) cout << "orz";
	else cout << t;
}

Kruskal 重构树【NOIP2018】T1

最短路

模板： P4779 【模板】单源最短路径（标准版）

Dijkstra算法

用于非负边权的单源最短路求解。

为什么不能处理负权呢？

因为当把一个节点选入集合 \(S\) 时，即意味着已经找到了从源点到这个点的最短路径，但若存在负权边，就与这个前提矛盾，可能会出现得出的距离加上负权后比已经得到 \(S\) 中的最短路径还短。（无法回溯）

流程

将结点分成两个集合：已确定最短路长度的点集（记为 \(S\) 集合）的和未确定最短路长度的点集（记为 \(T\) 集合）。一开始所有的点都属于 \(T\) 集合。

初始化 ，其他点的\(dis()\)均为 $ +\infty$。

然后重复这些操作：

1. 从 集合中，选取一个最短路长度最小的结点，移到 集合中。
2. 对那些刚刚被加入 集合的结点的所有出边执行松弛操作。

直到 集合为空，算法结束。

代码实现

1.暴力

不使用任何数据结构进行维护，每次 2 操作执行完毕后，直接在 \(T\) 集合中暴力寻找最短路长度最小的结点。

2.二叉堆优化

每成功松弛一条边 \((u, v)\)，就将 插入二叉堆中（如果 \(v\) 已经在二叉堆中，直接修改相应元素的权值即可），1 操作直接取堆顶结点即可。共计 \(m\) 次二叉堆上的插入（修改）操作，\(n\) 次删除堆顶操作。

int dist[maxn], v[maxn];
priority_queue<pair<int, int> > q;
void dijkstra(){
	memset(dist, 0x3f, sizeof(dist));
	memset(v, 0, sizeof(v));
	dist[s] = 0;
	q.push(make_pair(0, s));
	while(!q.empty()){
		int x = q.top().second, d = q.top().first; q.pop();
		if(v[x]) continue;
		v[x] = 1;
		for(int i = head[x]; i; i = e[i].nxt){
			int y = e[i].v, z = e[i].w;
			if(dist[y] > dist[x] + z){
				dist[y] = dist[x] + z;
				q.push(make_pair(-dist[y], y));
			}
		}
	}
}

这里借鉴了李煜东的《算法竞赛进阶指南》，通过存负值来保证小根堆性质，也可手写一个结构体

DP 的思想

\(f[l][i]\)表示是否有 \(s\) 到i的，长度为 \(l\) 的路径。

正向转移，枚举边\((i,j,w)\)：\(f[l+w][j]|=f[l][i]\)

优化：只找 dp 值为1，且没有更短的状态更新。

最短路数量：\(f[l+w][j] += f[l][i]\), 加一个cnt数组，如果更新了最短路，更新cnt

SPFA

\(SPFA\) 是 \(Bellman-Ford\) 算法的优先队列优化，其复杂度在一般情况下为 $ O (km)$ ,其中\(k\)通常是一个很小的常数，但在一些极端情况下其复杂度可退化至 $ O(nm)$,和暴力的BF一样。

所以，它死了。

但是还是挺好用的。

void spfa(){
    vis[0] = 1;
	q.push(0);
	while (!q.empty()) {
	    int u = q.front(); q.pop(); vis[u] = 0;
	    if (tot[u] == n - 1) { cout << -1; return 0; }
	    tot[u]++;
	    for (int i = head[u]; i; i = e[i].nxt)
	        if (dis[e[i].v] < dis[u] + e[i].w) {
	            dis[e[i].v] = dis[u] + e[i].w;
	            if (!vis[e[i].v]) vis[e[i].v] = 1, q.push(e[i].v);
	        }
	}
}	

一个点最多被入队 \(n\) 次

• 本身是个BFS，因此经过的边数少的路径会先进队列
• 出队再入队之后经过的边数必定加一
• 最短路长度不超过n

Floyd

可求多源最短路。

虽然 \(Floyd\) 的复杂度是 \(\Theta(n^3)\) ,但是可以求多源最短路（所以其存在是有意义的）

\(f[k][i][j]\) 表示从 \(i\) 到 \(j\) 只经过 \(1\) ~ \(k\) 的点的最短路。

状态转移：不经过 k：\(f[k−1][i][j]\)

经过 k：\(f[k−1][i][k]+f[k−1][k][j]\)

可以省略第一维，因此 \(f[i][j]=min⁡(f[i][j],f[i][k]+f[k][j])\)

for(int k = 1; k <= n; k++)
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
            f[i][j] = min(f[i][k] + f[k][j], f[i][j]);

K短路

A*乱搞

正解：可持久化可并堆

图的连通性相关

缩点

模板：P3387 【模板】缩点

这道题如果没有环的话用拓扑排序就可以了，然而这道题是有环的。这些存在从 \(x\) 到 \(y\) 的路径，也存在从 \(y\) 到 \(x\) 的路径，这叫做强连通分量。

对于每个连通分量，我们可以把它缩成一个点，因为如果这个连通分量中有一个点可以经过，那么整个连通分量也可以经过，也就是说，选了这个连通分量中的一个点，其他点也选上才是最优的。

缩完点后就是一张新的图，我们在这张新图上拓扑即可。

下面是缩点和建图代码：

void add(int u, int v){
	e[++cnt].v = v, e[cnt].u = u;
	e[cnt].nxt = head[u], head[u] = cnt;
}
int dfn[maxn], low[maxn];
int s[maxn];
int n, m;
int tme, top;
int p[maxn], sd[maxn], in[maxn], vis[maxn];
void tarjan(int x){
	low[x] = dfn[x] = ++tme;
	s[++top] = x, vis[x] = 1;
	for(int i = head[x]; i; i = e[i].nxt){
		int v = e[i].v;
		if(!dfn[v]){
			tarjan(v);
			low[x] = min(low[x], low[v]);
		}
		else if(vis[v]) low[x] = min(low[x], dfn[v]);
	}
	if(dfn[x] == low[x]){
		int y = 0;
		while(y = s[top--]){
			sd[y] = x;
			vis[y] = 0;
			if(x == y) break;
			p[x] += p[y];
		}
	}	
}
int d[maxn];

	cin >> n >> m;
	for(int i = 1; i <= n; i++) sd[i] = i;
	for(int i = 1; i <= n; i++) cin >> p[i];
	for(int i = 1; i <= m; i++){
		int u ,v ; cin >> u >> v;
		add(u, v);
	}
	for(int i = 1; i <= n; i++) if(!dfn[i]) tarjan(i);
	for(int i = 1; i <= m; i++){
		int x = sd[e[i].u], y = sd[e[i].v];
		if(x != y){
			e2[++cnt2].nxt = head2[x];
			e2[cnt2].v = y;
			e2[cnt2].u = x;
			head2[x] = cnt2;
			in[y] ++;
		}
	}

割点

P3388 【模板】割点（割顶）

点双连通分量

概念

在一张连通的无向图中，对于两个点 \(u\) 和 \(v\)，如果无论删去哪个点（只能删去一个，且不能删 \(u\) 和 \(v\) 自己）都不能使它们不连通，我们就说 \(u\) 和 \(v\) 点双连通。

若一张无向连通图不存在割点，则称它为点双连通图。

对于一张无向图，其极大点双连通子图（就是说不存在比它更大的子图使得这个子图是一个点双连通图）被称为点双连通分量。

无向连通图是“点双连通图”，当且仅当满足下列两个条件之一：

1）图的顶点不超过 \(2\) 个；

2）图中任意两个点都同时包含在一个简单环中。“简单环”指的是不相交的环。

——摘自李煜东《进阶指南》

具体证明可以看《进阶指南》，本蒟蒻不在这里做搬运工了。（逃）

求法

与边双不一样的是，点双并不是删除割点后图中剩余的连通块。
另外：桥虽然不属于任何边双，但割点可能属于多个点双。

另外，与边双连通分量不同的是，点双连通分量不具有传递性,也就是：如果 \(x\) 与 \(y\) 双连通且 \(y\) 与 \(z\) 双连通， 其实 \(x\) 与\(z\) 不是双连通的。

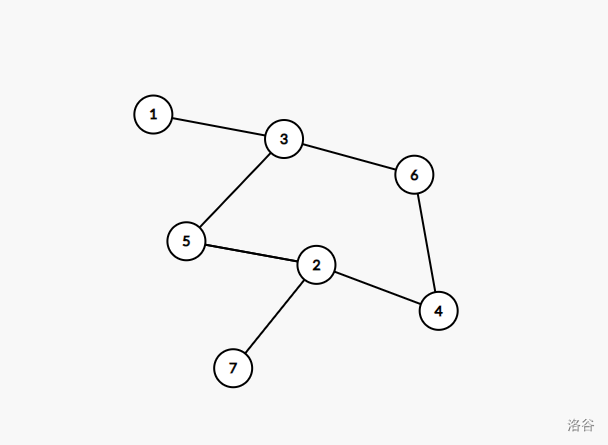
如上图，对于样例四，割点为 \(2\)，\(3\)， 而这两个割点又分别属于多个点双。

求点双连通分量仍然是用 Tarjan。

Tarjan 算法是什么呢？ Tarjan 算法是以美国著名计算机学家 Robert Tarjan 的名字命名的，能够在线性时间内求出无向图的割点与桥（其实还有个与有向图连通性相关的 Tarjan 算法可以求缩点），进而去求出图的双连通分量的算法。

其实 Tarjan 本质就是深搜，同时在深搜时维护时间戳、追溯值等信息和一个栈，通过一些法则来求割点等。

时间戳：时间戳就是在遍历整个无向图时，每个节点第一次被访问的顺序，我们记作 \(dfn(x)\) ;

追溯值： Tarjan 算法引入追溯值 \(low(x)\) ，将 \(low(x)\) 定义为以 \(x\) 为根的子树中 \(dfn(x)\) 与通过一条不在搜索树上的边，到达搜索树中 \(x\) 子树的点的 \(dfn(x)\) 的最小值。

同时，Tarjan 算法还维护一个栈，这个栈是用来维护当前路径上的节点的。先放上这个栈的维护规则，这个从各大网站上一搜就能搜到：

1. 在每个节点第一次访问时，就将它入栈；

2. 对于 \(x\) 的任意可以到达的节点 \(y\)， 当割点判定 \(dfn(x) \leqslant low(y)\) 成立时，无论 \(x\) 是否为根，都要从栈顶不断弹出节点，直到 \(y\) 弹出，并且让弹出的节点与 \(x\) 一起构成一个点双。

至于这个栈是干什么的呢？我们仍然用样例四模拟一下：

当访问到 \(7\)，然后回溯时，发现 \(2\) 是个割点。

此时的栈： 1 3 6 4 2 7

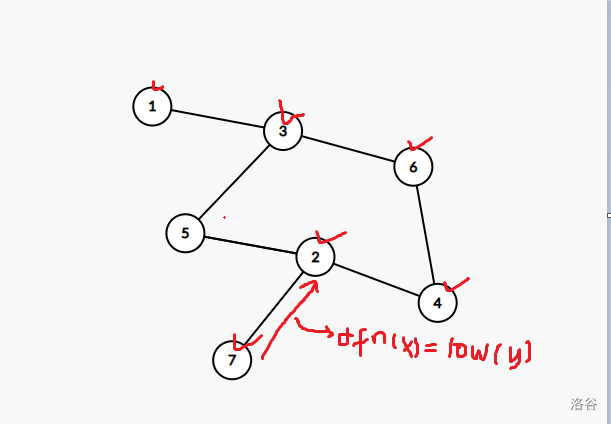
我们将它弹出，让 \(7\) 与 \(2\) 构成一个点双，弹出后： 1 3 6 4 2；

通过 \(5\) 访问到 \(3\) ，回溯时发现符合割点判定定理，此时的栈： 1 3 6 4 2 5

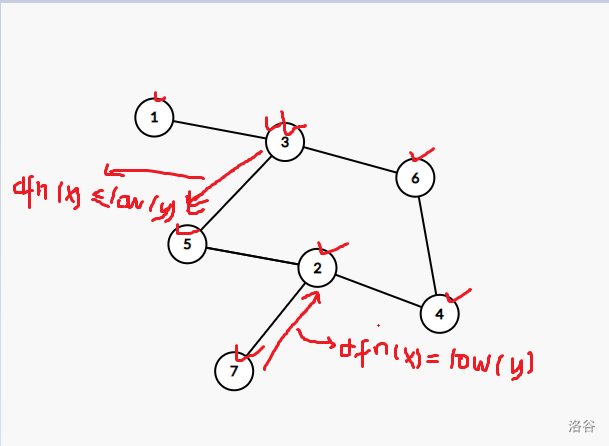
我们把它弹出，弹出元素为： 5 2 4 6 ，让他们与 \(3\) 构成一个点双，剩余的栈： 1 3；

最后同理，在从 \(3\) 回溯到 \(1\) 时也符合割点判定定理，让 \(1\) 与 \(3\) 构成一个点双。

通过模拟，我们可以发现：其实这个栈维护的就是一些有一定连通性的节点，也就是这个栈中所存的节点所构成的图应该没有割点。而当有割点的时候呢？就让这个栈中的节点不断弹出，直到这个栈中没有割点为止，此时，弹出的节点与先前那个割点一同构成一个点双。

为什么能这样呢？我们再返回点双连通分量的定义：对于两个点 \(u\) 和 \(v\)，如果无论删去哪个点都不能使它们不连通，这说的不就是要有一定的封闭性吗！

再看割点的定义：在无向连通图中，如果将其中一个点以及所有连接该点的边去掉，图就不再连通，那么这个点就叫做割点。那么我们将无向连通图中的割点去掉，在它形成的几个子图中再分别将割点再加回去，不就是一张无向连通图了吗！

例如还说样例四，将割点去掉后再根据上文所说分别在子图中加入割点的话，就成了这个样子：

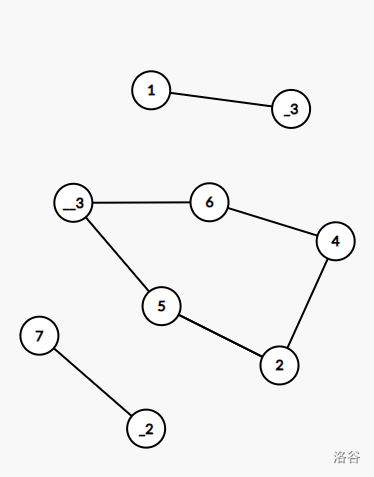
这不就是我们所要求的点双连通分量吗！所以说，对于一张无向连通图，将其割点去掉若有 \(n\) 张子图，将每个割点分别在这 \(n\) 子图上加上，就构成了 \(n\) 张没有割点的无向连通图，也就是找到了这 \(n\) 个点双连通分量。 其实上面说的一堆应该就是这个意思（个人见解）。

另：一个孤立点也是一个点双连通分量哦。

代码

最后贴上代码，上面有一些细节。

#include <bits/stdc++.h>
#define maxn 100005
using namespace std;
inline int read(){
    int x = 0 , f = 1 ; char c = getchar() ;
    while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; } 
    while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; } 
    return x * f ;
}
int n, m;
struct edge{
	int u, v, nxt;
}e[5 * maxn];
int head[maxn], cnt;
void add(int u, int v){
	e[++cnt].v = v, e[cnt].nxt = head[u], head[u] = cnt;
}
int dfn[maxn], low[maxn], tot, s[maxn], top, tme, root;
vector<int> dcc[maxn];
int cut[maxn];
void tarjan(int x){
	dfn[x] = low[x] = ++tme;
	s[++top] = x;
	if(x == root && head[x] == 0){		//这些说明x是一个孤立点，孤立点自身是一个点双 
		dcc[++tot].push_back(x);
		return;
	}
	for(int i = head[x]; i; i = e[i].nxt){
		int y = e[i].v;
		if(!dfn[y]){
			tarjan(y);
			low[x] = min(low[x], low[y]);	//更新追溯值
			if(low[y] >= dfn[x]){	//符合割点判定定理，弹栈
				tot++;
				int k;
				do{
					k = s[top--];
					dcc[tot].push_back(k);
				}while(k != y);
				dcc[tot].push_back(x);
			}
		}
		else low[x] = min(low[x], dfn[y]);
	}
}
int main() {
	n = read(), m = read();
	while(m--){
		int u = read(), v = read();
		add(u, v), add(v, u);
	}
	for(int i = 1; i <= n; i++){
		root = i;
		if(!dfn[i]) tarjan(i); 
	}
	cout << tot << endl;
	for(int i = 1; i <= tot; i++){
		cout << dcc[i].size() << " ";
		for(int j = 0; j < dcc[i].size(); j++){
			cout << dcc[i][j] << " ";
		}
		cout << endl;
	}
}

```cpp
int n, m, cntb, cntw, flag;
int nw[maxn], nb[maxn], vis[maxn], in[maxn], col[maxn];
int sum[2];

struct edge {
	int v, nxt;
}e[10 * maxn];
int head[maxn], cnt;

void add(int u, int v) {
	e[++cnt].v = v;
	e[cnt].nxt = head[u], head[u] = cnt;
}

void dfs(int x, int color) {
	vis[x] = 1;
	col[x] = color;
	sum[color] ++;
	for (int i = head[x]; i; i = e[i].nxt) {
		int y = e[i].v;
		if (vis[y]) {
			if (col[y] == color) flag = 1;
			continue;
		}
		dfs(y, color ^ 1);
	}
}

signed main() {
	n = read(), m = read();
	for (int i = 1; i <= m; i++) {
		int u = read(), v = read();
		add(u, v), add(v, u);
		in[u] ++, in[v] ++;
	}
	int ans = 0;
	for (int i = 1; i <= n; i++) {
		if (!vis[i] && in[i]) {
			sum[0] = sum[1] = 0;
			dfs(i, 0);
			if (flag) {
				cout << "Impossible";
				return 0;
			}
			ans += min(sum[0], sum[1]);
		}
	}
	if (flag) cout << "Impossible";
	else cout << ans;
}