Python: Guess and Check algorithms, Approximate solutions, Bisection method

 

判断一个整数是否为完全立方数 cubic number:

 

 

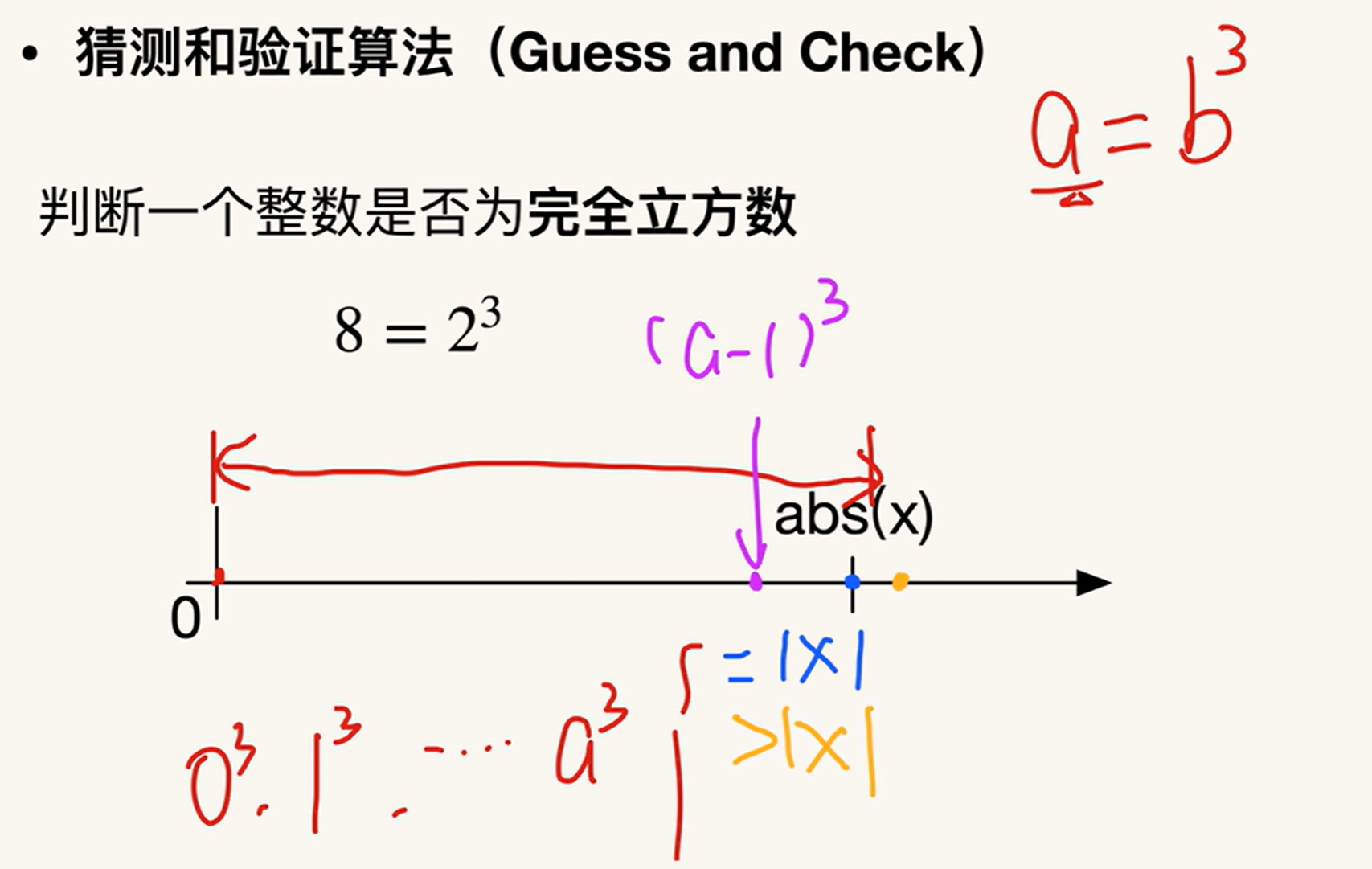
import math

cubical = int(input('number: '))


def is_cubical(cubical: int):
    n = math.ceil(pow(cubical.__abs__(), 1 / 3))
    # for v in range(abs(cubical) + 1):
    for v in range(n + 1):
        if pow(v, 3) == abs(cubical):
            if cubical < 0:
                return True, -v
            else:
                return True, v
    return False, None


print(is_cubical(cubical))

 

Approximation: 近似算法

 

 

 

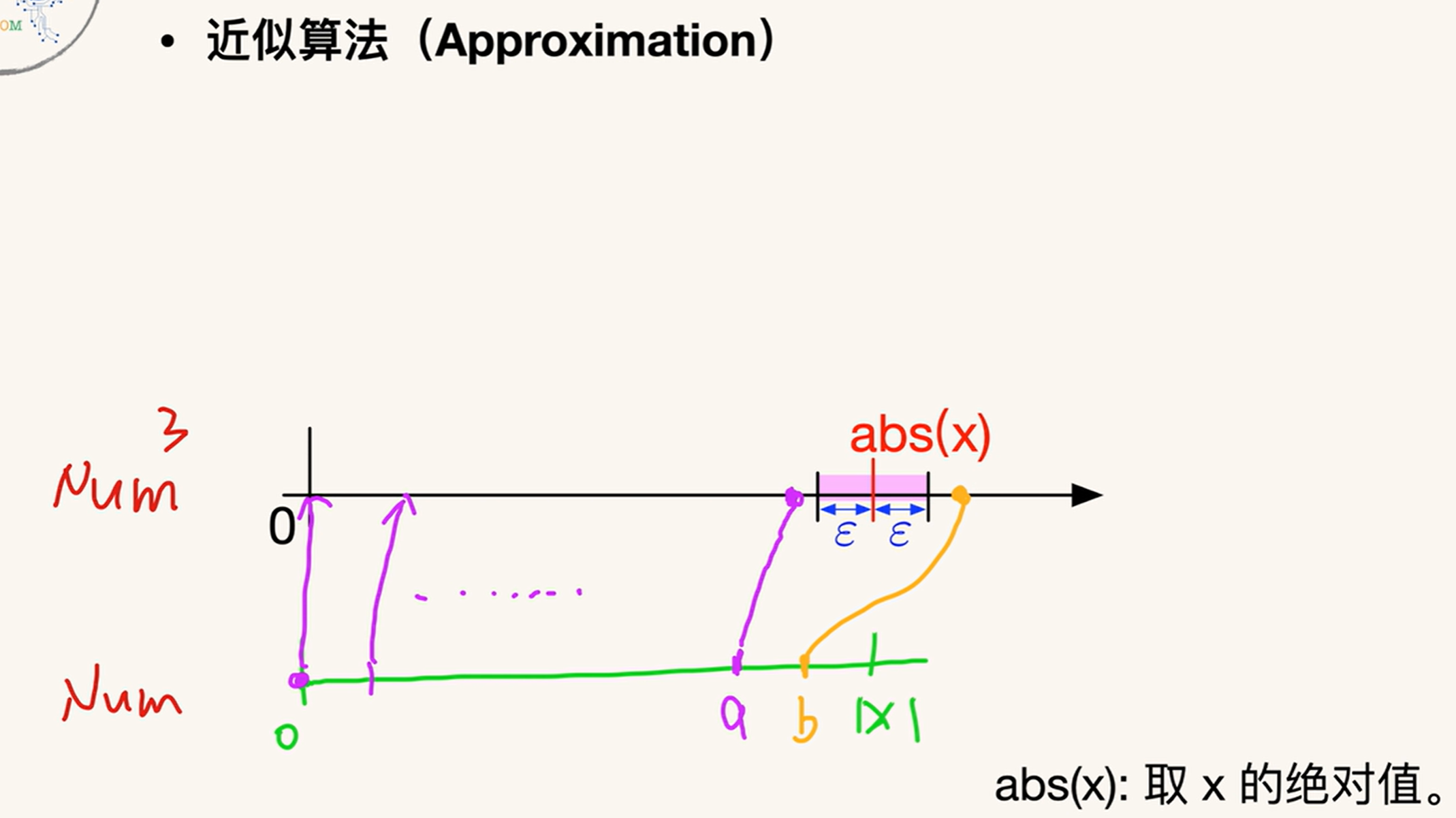
import math

cubical = float(input('number: '))


def cube_root(cubical: float):
    guess = 0.0
    increment = 0.0001
    epsilon = 0.001  # the precision must below epsilon, need to less than increment
    count = 0
    while abs(pow(guess, 3) - abs(cubical)) >= epsilon and guess <= abs(cubical):
        guess += increment
        count += 1

    if abs(pow(guess, 3) - abs(cubical)) >= epsilon:
        return None, count
    else:
        if cubical < 0:
            return -guess, count
        else:
            return guess, count


print(cube_root(cubical))

 

Bisection 二分法:

 

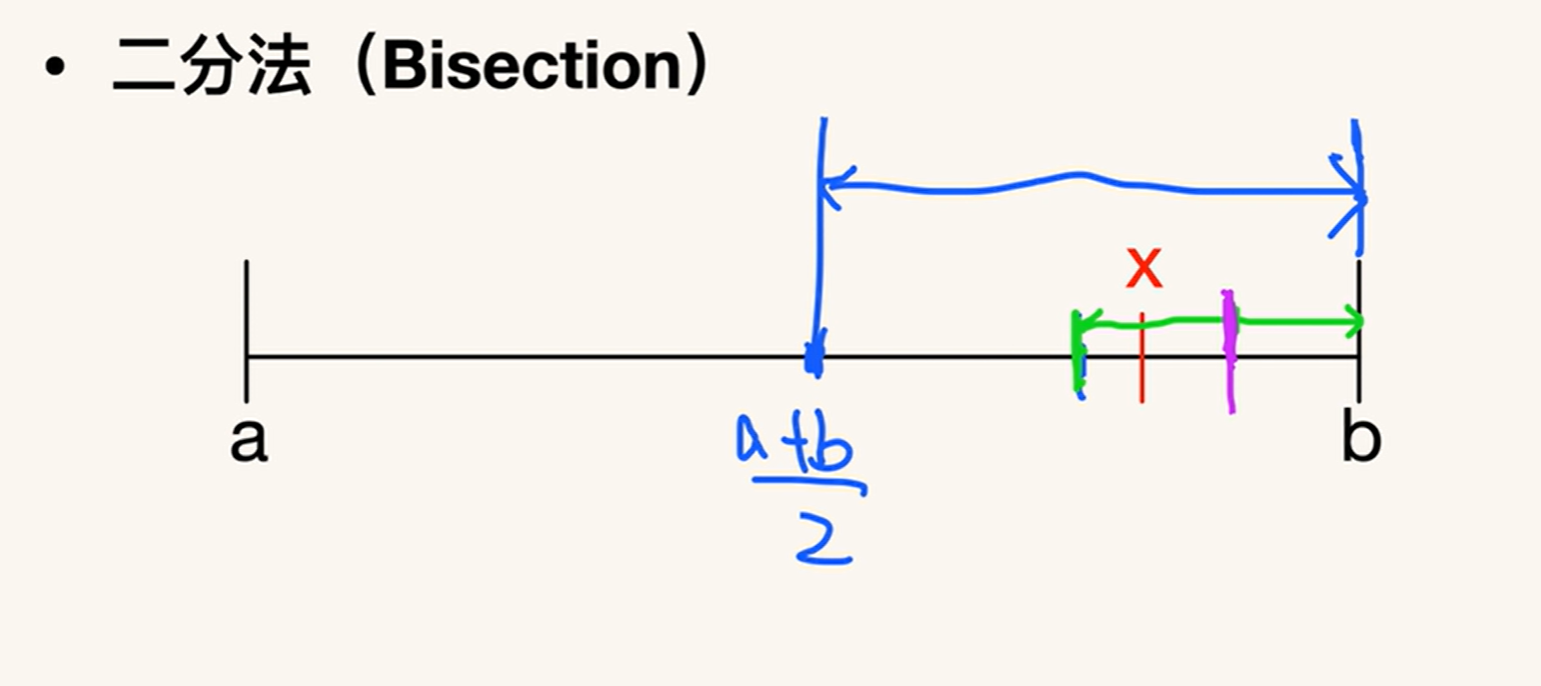
cubical = float(input('number: '))


def cube_root(cubical: float):
    epsilon = 0.001
    low = 0.0
    high = abs(cubical)
    middle = (low + high) / 2
    while abs(pow(middle, 3) - abs(cubical)) >= epsilon:
        if pow(middle, 3) > abs(cubical):
            high = middle
        else:
            low = middle
        middle = (low + high) / 2
    return middle


print(cube_root(cubical))