《人工神经网络》第4章 Hopfield网络模型

Hopfield 网络模型

相互连接型的神经网络模型，简称为 HNN （Hopfield Neural Network），解决了具有 NPC 复杂性的旅行商问题（TSP）

对比：

MP模型、感知器模型、自适应神经元Adaline、EBP网络：属于前向神经网络。

学习观点：是强有力的学习系统，结构简单，易于编程

系统观点：静态的非线性映射，通过简单非线性处理单元复合映射获得复杂的非线性处理能力，缺乏反馈，不是强有力的动力学系统

Hopfield：反馈型神经网络

具有很强的计算能力，注重系统稳定性，稳定性是具有联想记忆功能神经网络模型的核心，学习记忆过程就是系统向稳定状态发展的过程。

 

4.1  离散型Hopfield神经网络

反馈神经网络作为非线性动力学系统，有丰富的动态特性：稳定性、极限环、奇怪吸引子（混沌）等。

两个重要特性：1、系统有若干个稳定状态，若从某一个初始状态开始运动，系统总可以进入其中一个稳定状态；2、系统的稳定状态可以通过改变各个神经元之间的连接权值得到。

网络稳定性由能量函数判定

 

4.1.1  离散 Hopfield 神经网络模型

离散 Hopfield 神经网络是一个离散时间系统，工作原理：

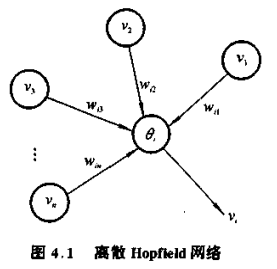
设有 n 个神经元，V 是神经网络的状态矢量，vi 是第 i 个神经元的输出，输出值是0或1的二值状态。对任意神经元 i ，v₁、v₂，... 、v_n 是第 i 个神经元的输入，他们对神经元的影响程度用连接权 w_i1、w_i2、... 、w_in 表示，θ_i 是阈值，则有，

Hopfield 网络是对称网络，w_ij = w_ji 。当 w_ii = 0 时，称为无自主反馈的离散 Hopfield 网络，反之，称为有自主反馈的Hopfield网络。

Hopfield 网络两种工作方式：

1、异步方式：在任一时刻 t ，只有某个神经元按式（4.1）发生变化，而其余 n - 1 神经元保持不变

2、同步方式：在任一时刻 t ，有部分神经元按式（4.1）变化（部分同步）或所有神经元按式（4.1）变化（全并行同步）

[ 定义4.1 ]  若神经网络从 t = 0 的任意一个初始状态 V(0) 开始，存在一个有限的时刻，从该时刻后，神经网络状态不再发生变化，即：

　　　　V( t + Δt ) = V( t ) ，Δt > 0

则称网络是稳定的。

 

4.1.2  网络的变化

对于 n 节点的 HNN 有 2ⁿ 个可能的状态，网络状态用一个包含 0 和 1 的矢量表示。每个时刻整个网络处于一个状态。状态变化采用随机异步更新，随机的选择下一个要更新的神经元，且允许所有的神经元具有相同的平均变化率。

节点状态更新的三种情况：由 0 变为 1 、由 1 变为 0 、状态保持不变

按照单元异步更新的工作方式，某一时刻网络中只有一个节点被选择更新状态，当该节点状态变化时，网络状态就以某一概率转移到另一种状态；当该节点状态保持不变时，网络状态更新的结果保持前一时刻状态。通常，网络从某一初始状态开始经过多次更新后，才可能到达某一稳态。

异步状态更新的好处：

1、算法容易实现，每个神经元节点有自己的状态更新时刻，不需要同步机制

2、以串行的方式更新网络的状态可以限制网络的输出状态，避免不同稳态以等概率出现

一但给出了 HNN 的权值和神经元的阈值，网络的状态转移序列就确定了。

Th 4.1 若神经网络的连接矩阵 W 是零主对角元素的对称矩阵，即满足 wij = wji 且 wii = 0, i = 1，2，... ，n，网络状态按串行异步方式跟新，网络状态必收敛于状态空间中的某一个稳定状态。

 

4.1.3  能量函数

能量函数用来描述系统的稳定性

4.1.3.1  能量函数的定义

 

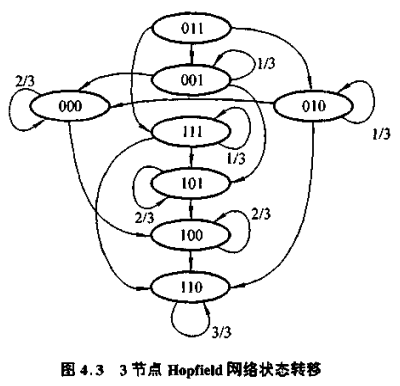
由上图可发现，状态转移关系规律：任意一个状态要么在同一“高度”变化，要么从上到下转移。

Hopfield 网络模型是一个多输入、多输出、带阈值的二态非线性动力系统。

在满足一定的参数条件下，某种能量函数在网络运行过程中是不断降低、最后趋于稳定平衡状态。这种能量函数作为网络计算求解的工具，被称为计算能量函数。

Hopfield 网络状态变化分析的核心是对每个网络的状态定义一个能量 E ，任意一个神经元节点状态发生变化时，能量 E 都将减小。

假设第 i 个神经元节点状态 v_i 的变化量为 Δv_i ，相应的能量变化量记为 ΔE_i 。所谓能量Ei随状态变化而减小意味着 ΔE_i 总是负值。

两种情况：

(1) 当状态 vi 由 0 变为 1 时， Δv_i > 0 ，必有 Net_i > 0

(2) 当状态 vi 由 1 变为 0 时， Δv_i < 0 ，必有 Net_i ≤ 0

所以，Δv_i 和  Net_i 的积总是正的。则：

　　　　ΔE_i = - Net_i Δv_i 

即：

 

式 (4.2) 出现 1/2 因子，是因为离散 Hopfield 网络模型中，w_ij = w_ji ，如果直接求 ΣE_i ，会使 E_i 中每一项都计算两次。

 

Th 4.2  在离散 Hopfield 模型状态更新过程中，能量函数 E 是随状态变化而严格单调递减的。

Th 4.3  离散 Hopfield 模型的稳定状态与能量函数 E 在状态空间的局部最小点是一一对应的。

 

4.1.3.2  设计能量极小点

当网络的能量极小点被选择和设定时，网络具有的能力才能发挥作用。

能量极小值点的分布由网络的连接权值和阈值所决定。

设计极小值点的核心：如何获取一组合适的参数值。

两种方法：

1、根据求解问题的要求，直接设计出所需要的连接权值——静态学习方法，对于一个具体应用而言，权矩阵为定常矩阵，如 TSP 求解等

2、通过提供的附加机制来训练网络，使其自动调整连接权，产生期望的能量极小点——动态学习方法，如联想记忆的实现等

 

4.1.4  离散 Hopfield 网络的学习与联想记忆

Hopfield 网络用于计算时，其权矩阵给定为 W ，目的是寻找具有最小能量 E 的网络稳定状态；作为记忆的学习时，稳定状态是给定的，通过网络的学习求合适的权矩阵 W（对称阵）。一旦学习完成后，以计算的方式进行联想。

只要 Hopfield 神经网络的权值矩阵 W 是对称的，其网络状态最终将收敛到由 W 及其阈值 θ 所定义的能量函数的极小点，就可以实现联想记忆功能。

联想记忆：预先把要记忆的完整模式以一定方式形成记忆矩阵，然后把他们记忆到计算机中。之后，当网络输入不完整模式时，可以通过记忆矩阵和阈值函数的作用，在网络的输出端得到完整的模式。

Hopfield 网络，可以采用 Hebb 学习规则和误差型学习算法

基于 Hebb 学习规则的 Hopfield 网络的学习：对给定的 M 个模式，Hopfield 网络学习按 Hebb 学习算法进行：

 

按上述规则求出权矩阵后，可以认为网络已经将这 M 个模式存入网络的连接权中。

在联想过程中，先给出一个原始模式 m⁰ ，使网络处于某种初始状态下，用网络方程动态运行，最后达到一个稳定状态。如果此稳定状态对应已存贮的 M 个模式中某个模式 m^k ，则称 m^k 是由模式 m⁰ 联想起来的。

Hopfield 网络用于记忆联想，是受其记忆容量和样本差异制约的。当记忆的模式较少，且模式之间的差异较大，则联想的结果就比较正确；当需要记忆的模式较多，容易引起混淆，网络达到的稳定状态往往不是已记忆的模式；当需要记忆的模式之间较为相近时，网络就不能辨别出正确的模式，甚至连自身都会搞错，即使用已记忆的模式作为联想模式（自联想），也可能会出错。

网络的记忆容量问题：

 

 

 

4.2  连续型 Hopfield 神经网络

由简单电子线路实现的连续时间神经网络模型

4.2.1  模型结构

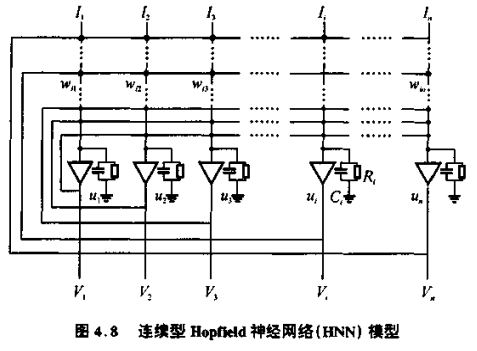
将离散的 Hopfield 神经网络模型扩展到连续时间的动力学模型，其网络的连接方式不变，仍然是全互联对称结构。连接型 Hopfield 神经网络（ HNN ）如下图所示

 

其动力模型如下：

与离散的 HNN 相比较，上式多了一个一阶惯性环节（ 连续时间动力学方程 ）。实际上，离散的 HNN 中直接有 ui = si 。特别注意：函数 f(•) 是连续的 S 型函数，不再是二值函数。

Hopfield 用模拟电路设计了一个连续 Hopfield 神经网络的电路模型，如下图表示其中由运算放大器电路实现的一个节点的模型

 

 

网络节点神经元由运算放大器实现。该模型，电路方程是：

 

 

式 ( 4.12 ) 中，u_i 是神经元 i 的内部状态；v_i 是神经元 i 的输出；w_ij 是神经元 i，j 之间的连接权。该式就是系统的动态方程。

动态方程描述了神经元 i 的输出和其内部状态 u_i 之间的关系。连续型 Hopfield 网络实质上是一个连续的非线性动力学系统，由一组非线性微分方程来描述。给定初始状态 v_i (0),（ i = 1，2，...，n ）通过求解非线性微分方程组即可求得网络状态的运动轨迹。若系统是稳定的，则它最终会收敛到一个稳定状态。若用模拟电路的硬件来实现此模型，求解非线性微分方程的过程将由该电路自动完成，求解速度非常的快。

 

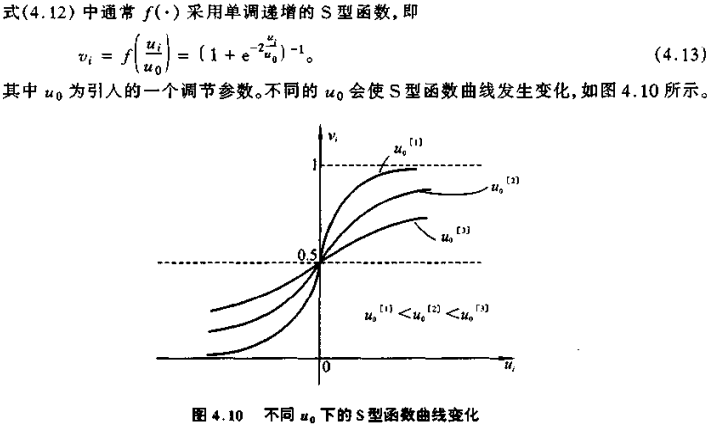
当 u0 不断减小时，S 型函数之间和一个阶跃函数靠近。

 

4.2.2  稳定性分析

和离散的 Hopfield 网络一样，Hopfield 对连续型的模型定义了一个 Lyapunov 意义下的计算能量函数：

 

 

连续型 Hopfield 神经网络特性：

1、系统在运行过程中，能量函数会逐渐减小到某一极小状态

2、系统的极小状态一般不止一个，存在有限个平衡点

3、连续型 Hopfield 神经网络可以用模拟电路实现。电路中的放大器和电阻电容等器件的电气特性在物理上对生物神经网络的某些特征有较好的模拟

 

4.3  旅行商问题（ TSP ）的 HNN 求解

4.3.1  计算复杂性

计算复杂性（ Computational Complexity ）涉及计算问题求解的定量分析，用定量分析以确定解决某一类问题算法所需要的计算资源的限额。通常用 n 表示某一计算问题的规模大小。

算法：将问题一步一步解决过程的规则描述

衡量算法复杂度的方法：与计算时间有关的程序长度，并行计算时并发步的层数（程序的深度），所需要的存贮容量和执行算法所需要的时间等

图灵机模型

利用图灵机可以给算法复杂性下一个形式化的定义，即从输入 x 开始，到停机为止的运行步数，作为图灵机对输入 x 的时间复杂性。

对于任意长度小于等于 n 的输入，某一确定型图灵机从初始状态 q0 开始，在不超过 n 的多项式 p(n) 步停机，则称机器在 p(n) 时间内运行，或输入 x 在 p(n) 时间内接受。

用确定型图灵机在多项式时间内能解决的问题，或者说解决某一问题算法的时间复杂型为O (p (n))（ n 为问题的规模，p 为 n 的某一多项式表达），则称该问题为时间问题 P类。

对于时间复杂性为 p(n) 的计算问题，是易于用快速计算机在有限时间内解决的。

复杂性较高的问题：矩阵运算、FFT 运算、文件检索、数据排列、任务分配、路由选择等

当某种问题的计算复杂性大到不能用多项式的时间函数来表示时，称它具有指数复杂性（ Exponential Complexity）。呈指数增长的时间复杂性要比多项式时间复杂性大得多。

基本术语：

[ P类问题 ]  可以用多项式时间复杂性 O (p (n)) 的算法解决的问题，也就是在有限个 0 和 1 组成的符号串集合 {0，1} 中，那些为图灵机在多项式时间内所接受的子集。

如，时间复杂性 O（n），O（n²）

当多项式 p（n）的最大阶数 K 的数值较大时，随着规模 n 的增大，将会使问题的计算耗时相当大。但他们仍属于 P 类问题。

[ NP 问题 ]  一类不能用每一步都唯一确定的确定算法（ Deterministic Algorithms ）来解决计算难度较大的问题。它能用一种非确定算法（ Non-Deterministic Algorithms ）在多项式时间内加以解决。

非确定算法包含两级算法：第一级是猜想级，第二级是检验级。非确定图灵机（NTDM）在猜想阶段随机地选定一个 {0，1} 序列输入作为答案，在检验级阶段检查输入“是”的答案，然后输出“是”或者“不是”。如果在检验级阶段能以多项式时间进行“否”的检验，则称它属于 Co-NP 类。

[ NPC 问题 ]  NP 完全（ NP-Complete ）问题。

[ 超 NP 类问题 ]  除 P 类和 NP 类问题外，还有很多重要的问题，它们用非确定性图灵机也无法计算解决。这些被称为超 NP 类问题。