树上基础操作(直径 & 中心 & 重心 & 树上差分 & dfs序)
补一补。
树的直径
树上任意两节点之间最长的简单路径即为树的「直径」。一棵树可以有多条直径,他们的长度相等。
两种求法。
求法一
两遍 dfs,第一次 dfs 随便从一点 y 开始,dfs 到最远点 s,第二次从 s 开始 dfs 到最远点 t。(s,t)即为树的直径。
证明:如果 s 是直径的一端,那么 t 肯定就是另一端,只需要证 s 是直径的一端即可。
考虑反证,假设 s 不为直径的一端,然后多分几种情况,画画图去证。
(下述证明过程建立在所有路径均不为负的前提下。如果树上存在负权边,则证明不成立。故若存在负权边,则无法使用两次 DFS 的方式求解直径)

如果要记录直径有哪些点,记录一下每个点从哪个前驱点 dfs 过来即可。
求法二
树上每条简单路径一定都有最高点,可以考虑对这个最高点讨论。(从而避免讨论路径的起点终点,变成 O(n^2))
假设存在一条最长简单路径,最高点为 u,这个最长的简单路径只会是 u 拼接两段最长和次长的简单路径组成。
于是可以考虑树形 DP。设 d1[u], d2[u] 分别表示 u 为最高点时,最长/次长 简单路径长度。
换句话说,就是在 u 子树内的 最长/次长 简单路径。但是,两简单路径不能有公共部分。(因为基于上面的讨论需要)
正常转移即可。(事实上,可以把数组压成一个,但是没啥必要)
所以树形 DP 可以在存在负权边的情况下求解出树的直径。
如果要记录直径有哪些点,记录一下每个点从哪转移即可。
板子
一点理解:不需要用 d2[v] 更新 d2[u],因为 d1[v] 能更新 d2[u],就不用 d2[v] 更新了,d1[v] 更新不了 d2[u],d2[v] 更不能更新 d2[u]。
#include <bits/stdc++.h>
using namespace std;
const int N=500005;
struct node
{
int v, w;
};
int n, u1, v1, w1, d1[N], d2[N], ans=0;
vector<node> a[N];
void dfs(int u, int fa)
{
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i].v, w=a[u][i].w, t=0;
if (v==fa) continue;
dfs(v, u);
t=d1[v]+w;
if (t>=d1[u]) d2[u]=d1[u], d1[u]=t;
else if (t>d2[u]) d2[u]=t;
}
ans=max(ans, d1[u]+d2[u]);
}
int main()
{
scanf("%d", &n);
for (int i=1; i<n; i++)
{
scanf("%d%d%d", &u1, &v1, &w1);
a[u1].push_back({v1, w1});
a[v1].push_back({u1, w1});
}
dfs(1, 0);
printf("%d", ans);
return 0;
}
性质
转自:树的直径,树的中心性质整理 - dbxxx - 博客园(这里不是很详细,只摘录了一些比较人性好理解的部分,某些我任务不重要的没摘出来,链接提供的性质更详细)
下文的 ${u \leftrightsquigarrow s}$ 表示 u 到 v 的简单路径。$(a \sim b)$ 表示 a 到 b 的简单路径长度。
下文讨论都是基于树上所有边边权均为正
1.如果一个点 u 在一条直径 D 上,D 的端点是 s 和 t,那么 ${u \leftrightsquigarrow s}$ 和 ${u \leftrightsquigarrow t}$ 中较长的一定是一条从 u 出发的最长链。
比较显然。
2.从任意一个点出发,能到达的最远点一定是某条直径的端点。
上文证明过。
3.直径的端点一定都是叶子节点。
显然。
4.对于两棵树,如果第一棵树直径两端点为 (u,v),第二棵树直径两端点为 (x,y),用一条边将两棵树连接,那么新树的直径一定是 u,v,x,y 中的两个点。

5.一棵树上,一定存在一个点 $p$ 被这棵树的所有直径经过。

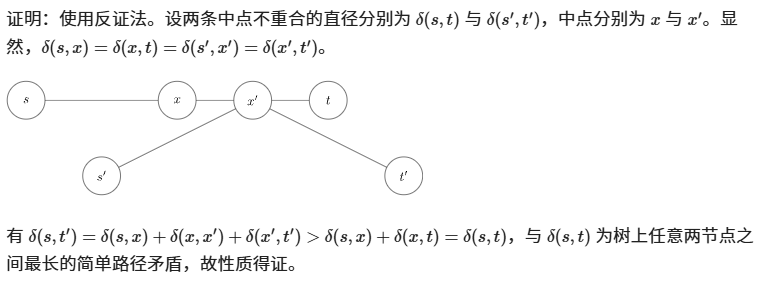
假设此时有三条直径,那一定交于同一点,因为如果三条直径分别交不同两点,那么一定存在两条直径不存在交点,根据上述证明,一定有一条直径是矛盾的。
所以多条直径一定同时交于一个或一个以上的点。
6.树的所有直径中点重合
例题
P2195(Code),类似性质4,这里可以把树的直径抽出来理解,这样就贪心的取两直径中点相连就好。
1.对于这种游戏策略题,可以考虑其中一位玩家的最优决策,另外一位的最优决策也可以跟着出来。最好的方法是手玩样例+详细的分类讨论+考虑极端情况。
2.树上的特殊点:树的直径中点,可以以最短长度覆盖整棵树。
其实这两题可以归到树的中心去。因为这些题同时都是一些关于树的中心的性质。
树的中心
详解
找到一个结点作为根,使得树的最长链最短。这个结点就是树的中心。
具体求法可以看:换根 DP - cn是大帅哥886 - 博客园
这里贴个板子:U392706
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+5, INF=1e18;
struct node
{
int v, w;
};
int n, u1, v1, w1, g[N][2], pre[N][2], up[N], f[N], mn=INF;
vector<node> a[N];
void dfs(int u, int fa)
{
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i].v, w=a[u][i].w, t=0;
if (v==fa) continue;
dfs(v, u);
t=g[v][0]+w;
if (t>=g[u][0]) g[u][1]=g[u][0], pre[u][1]=pre[u][0], g[u][0]=t, pre[u][0]=v;
else if (t>g[u][1]) g[u][1]=t, pre[u][1]=v;
}
}
void dfs2(int u, int fa)
{
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i].v, w=a[u][i].w;
if (v==fa) continue;
if (pre[u][0]!=v) up[v]=max(up[u], g[u][0])+w;
else up[v]=max(up[u], g[u][1])+w;
dfs2(v, u);
}
f[u]=max(g[u][0], up[u]), mn=min(mn, f[u]);
}
signed main()
{
scanf("%lld", &n);
for (int i=1; i<n; i++)
{
scanf("%lld%lld%lld", &u1, &v1, &w1);
a[u1].push_back({v1, w1});
a[v1].push_back({u1, w1});
}
dfs(1, 0);
dfs2(1, 0);
for (int i=1; i<=n; i++) if (f[i]==mn) printf("%d\n", i);
return 0;
}
性质
0.把一颗树的直径拎出来,那直径中点一定是中心。
证明还是毕竟显然,然后由此可以推出若干显然的性质:
1.树的中心不一定唯一,但最多有 2 个,且这两个中心是相邻的。
2.树的中心一定位于树的直径上。
3.树上所有点到其最远点的路径一定交会于树的中心。
4.当树的中心为根节点时,其到达直径端点的两条链分别为最长链和次长链。
5.当通过在两棵树间连一条边以合并为一棵树时,连接两棵树的中心可以使新树的直径最小。
6.树的中心到其他任意节点的距离不超过树直径的一半。
例题
鸽子了。
树的重心
详解
找到一个结点,删掉这个结点,树形成若干棵子树,使得这些子树中权值最大的最小。这个结点就是树的中心。
也可以考虑换根,毕竟删不同结点答案不一样。
我们发现删除 u,会形成 u 向上的一整颗子树,也就是整棵树除了 u 子树的部分,和 u 的若干子树。
对于 u 的若干子树,可以树形 DP 算。
对于 u 往上的一整颗子树可以利用加减法,即 u 子树外的整棵子树,是可以算的,具体的就是 n-sz[u]。
就做完了。
但是这里不用两遍 dfs,因为利用加减法时不需要知道父亲的结果,是能直接算的。
#include <bits/stdc++.h>
using namespace std;
const int N=5e4+5;
int n, u1, v1, sz[N], g[N], f[N], mn=N+5;
vector<int> a[N];
void dfs(int u, int fa)
{
sz[u]=1;
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i];
if (v==fa) continue;
dfs(v, u);
sz[u]+=sz[v], g[u]=max(g[u], sz[v]);
}
f[u]=max(g[u], n-sz[u]), mn=min(mn, f[u]);
}
signed main()
{
scanf("%d", &n);
for (int i=1; i<n; i++)
{
scanf("%d%d", &u1, &v1);
a[u1].push_back(v1);
a[v1].push_back(u1);
}
dfs(1, 0);
for (int i=1; i<=n; i++) if (f[i]==mn) printf("%d ", i);
return 0;
}
性质
转自 算法学习笔记(72): 树的重心 - 知乎,写的非常好,能看懂!!
(可以自己手推。大多用调整法去证是好证的)

1.以树的重心为根时,所有子树的大小(也可以说是最大子树大小)都不超过整棵树大小的一半。(常常利用该性质找重心)

2.树至多有两个重心。如果树有两个重心,那么它们相邻。此时树一定有偶数个节点,且可以被划分为两个大小相等的分支,每个分支各自包含一个重心。

3.树中所有点到某个点的距离和中,到重心的距离和是最小的;如果有两个重心,那么到它们的距离和一样。

4.在一棵树上添加或删除一个叶子,那么它的重心最多只移动一条边的距离。
更准确的说法:往树上增加或减少一个叶子,如果原节点数是奇数,那么重心可能增加一个,原重心仍是重心;如果原节点数是偶数,重心可能减少一个,另一个重心仍是重心。
配着图看证明就好理解很多:
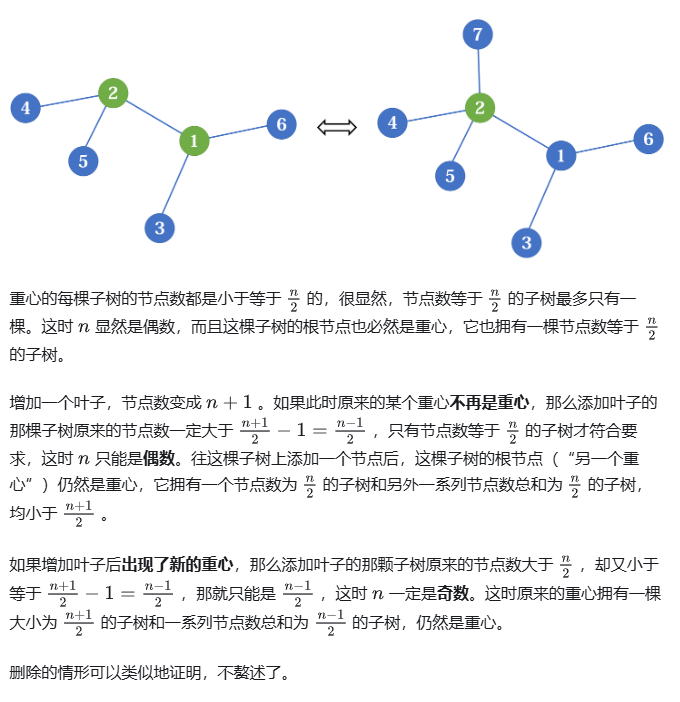
5.把两棵树通过一条边相连得到一棵新的树,那么新的树的重心在连接原来两棵树的重心的路径上。
6.以 u 为根的子树的重心,一定在以 u 的重儿子为根的子树的重心与 u 的连线上
例题
CF685B(Code),根据性质 6 能做,暴力跳就好。因为每次从上次跳到的地方接着跳,所以复杂度是 O(n)。
CF1406C(Code),根据性质 2 做,只要让调整两颗分出的子树大小不相等就行。
树的三心 小总结
1.树的直径和树的中心,求的时候不要弄混了。
2.求树的直径是不用换根的,可以直接树形DP的。但求树的中心/重心,就需要换根了,然后方法也都类似。
树上差分
序列差分
先看看简单回顾一下普通的序列差分。
差分数组:b[i]=a[i]-a[i-1],这样满足:b[1]+b[2]+b[...]+b[i]=a[i]。
然后就转化成前缀和。那么区间操作转化成单点操作(对 b[] 进行操作)。
板子:P2367
#include <bits/stdc++.h>
using namespace std;
const int N=5e6+5;
int n, p, a[N], x, y, z, b[N], Min=INT_MAX, s=0;
int main()
{
scanf("%d%d", &n, &p);
for (int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
b[i]=a[i]-a[i-1];
}
while (p--)
{
scanf("%d%d%d", &x, &y, &z);
b[x]+=z, b[y+1]-=z;
}
for (int i=1; i<=n; i++)
s+=b[i], Min=min(s, Min);
printf("%d", Min);
return 0;
}
例题:
P3948(Code),差分数组不要轻易取模,不然无法保证正确性!!!
P5026(Code),想复杂了,但也能做。解决区间加等差数列问题,可以用两个差分解决。
具体的,你顺序考虑差分就行。第一个差分把前缀和拆开,第二个差分利用拆出来的差分因为等差中间项都相等的,就可以维护了。比如:
等差数列 1 3 5 7 9 0 0
差分数组1 1 2 2 2 2 -9 0
差分数组2 1 -1
2 -2
-9 9
当然,你做出了第一个差分后,可以直接用线段树维护区间加,但是可能麻烦一点,不过适用于动态查询。
区间加等差数列板子:
void add(int L, int R, int p, int k) //区间 [L,R]+=p,p+k...p+(R-L+1)*k,其中 p 是首项,k 是公差
{
s[L]+=p, s[L+1]-=p;
s[L+1]+=k, s[R+1]-=k;
s[R+1]-=p+(R-L)*k, s[R+2]+=p+(R-L)*k;
}
AT_joi2017ho_a(Code)利用差分把区间修改转换为单点修改,从而只关注单点的信息。(当然你可以用线段树爆艹过去)
P1083,比较典就不写了,主要是要想到二分。然后再把区间加转换成单点加,就能做了。
P3943,咕咕咕。
树上点差分
类比序列差分,令 $d$ 为差分数组:
1.序列上求差分数组,也就是 $d_i=a_i-a_{i-1}$,当前数减去前面一个数,挂到树上相当于当前结点权值减去所有儿子结点权值。
即:$d_u=a_u- \sum\limits_{v=son(u)}a_v$。
2.序列上的对差分数组求前缀和就还原回原数组了,当前数加上前面一个数,挂到树上相当于当前结点权值加上所有儿子结点权值。也就是求子树和。
即:$a_u=d_u+ \sum\limits_{v=son(u)}d_v$(此时的 $d_v$ 是对 $v$ 做完子树和后的结果)
3.序列上对差分数组 $d_i$ 修改,相当于对原数组 $a$ 的后缀 $[i, n]$ 都进行了修改,挂到树上相当于对原数组 $a$ 的 $u \rightsquigarrow root$ 的路径上的结点权值都被修改了。
那么,修改 $s \rightsquigarrow t$ 路径上的权值(这里假设是加 val)。就等价于:
d[s]+=val, d[t]+=val, d[p]-=val, d[fa[p]]-=val(其中 $p$ 是 $s, t$ 的最近公共祖先)
板子:P3128
#include <bits/stdc++.h>
using namespace std;
const int N=5e4+5, M=22;
int n, m, u1, v1, dep[N], f[N][M], d[N], ans=0;
vector<int> a[N];
void dfs(int u, int fa)
{
dep[u]=dep[fa]+1, f[u][0]=fa;
for (int i=1; i<=20; i++) f[u][i]=f[f[u][i-1]][i-1];
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i];
if (v==fa) continue;
dfs(v, u);
}
}
int lca(int x, int y)
{
if (dep[x]<dep[y]) swap(x, y);
for (int i=20; i>=0; i--) if (dep[f[x][i]]>=dep[y]) x=f[x][i];
if (x==y) return x;
for (int i=20; i>=0; i--) if (f[x][i]!=f[y][i]) x=f[x][i], y=f[y][i];
return f[x][0];
}
void dfs2(int u, int fa)
{
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i];
if (v==fa) continue;
dfs2(v, u);
d[u]+=d[v];
}
}
int main()
{
scanf("%d%d", &n, &m);
for (int i=1; i<n; i++)
{
scanf("%d%d", &u1, &v1);
a[u1].push_back(v1);
a[v1].push_back(u1);
}
dfs(1, 0);
for (int i=1; i<=m; i++)
{
int p=0;
scanf("%d%d", &u1, &v1);
p=lca(u1, v1);
d[u1]++, d[v1]++, d[p]--, d[f[p][0]]--;
}
dfs2(1, 0);
for (int i=1; i<=n; i++) ans=max(ans, d[i]);
printf("%d", ans);
return 0;
}
树上边差分
类似边权转点权的技巧,把边塞进点里。这里应该把 $(u, v)$ 这条边塞进 $v$ 点,即儿子结点。很好理解,塞进父亲结点的话,一个点可能对应多条边,不好处理。
然后就和点差分一样了嘛。所以有以下式子:
$d_u=w(u, fa) - \sum\limits_{v=son(u)}w(u, v)$
$w(u, fa)=d_u + \sum\limits_{v=son(u)}w(u, v)$
你把边还原回去就好理解了,相当于一个结点应该对应着连向他父亲的那条边,且这条边是唯一的。
那么,修改 $s \rightsquigarrow t$ 路径上的权值(这里假设是加 val)。就等价于:
d[s]+=val, d[t]+=val, d[p]-=2*val(其中 $p$ 是 $s, t$ 的最近公共祖先)
和点差分类似,就是把上面的式子实现出来,比较容易就不贴板子了。
例题
P3258 (Code)树上点差分的板,但要注意 corner case。
P2680(Code)树上边差分+二分,其实也还好,能想到就不难,但是还要卡常。调一调二分边界就好。
转化题意的时候要转化完整,尽可能往典型题目转化,另外对二分啥的敏感一些,对于可能出现的“最大值最小”等等就应该往二分考虑。
DFS 序
代码可能要先鸽子了。但是思路已经非常完善。
注意,比较卡常,可以用树剖求 LCA+树状数组。
详解
DFS 序就是将树的节点按照先根的顺序遍历得到的节点顺序,如下:
void dfs(int u, int fa)
{
st[u]=++tim, pos[tim]=u;
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i];
if (v==fa) continue;
dfs(v, u);
}
en[u]=tim;
}
性质:一个子树全在一个连续的区间内,然后就能在 dfs 序上建立树状数组和线段树。
然后对于树上链修改,可以配合着树上差分。所以应该没什么难度。
点修改,子树和查询
转换成 dfs 序后变成:单点修改+区间查询,可以树状数组。
子树修改,子树查询
转换成 dfs 序后变成:区间修改+区间查询,可以线段树。
树链修改,点查询,子树和查询
#146. DFS 序 3,树上差分 1 - 题目 - LibreOJ
对于链修改+点查询,用树上差分可以转换为:单点修改+区间查询(子树和查询)
但是!原题要求的子树和查询,怎么处理?类比树状数组的处理,推式子,再优美式子,转换成好维护的形式。
考虑子树 u 的子树和,会由若干个子树内结点的值相加组成,我们只需要考虑某个结点 k 对 u 的贡献即可。但是经过差分,结点 k 的值要再求一遍 k 的子树和才能得来。
容易推出 k 对 u 的贡献为:(dep[k]-dep[u]+1)*val[k],拆式子变成 val[k]*dep[k]-val[k]*(dep[u]-1)。
容易发现 dep[u]-1 是定值,所以这个式子后半边可以维护 val[k] 的和,也就是区间查询,然后再乘上 (dep[u]-1) 即可。
前半边呢,再对于每个 k 维护 val[k]*dep[k] 就好,然后相当于区间查询。
所以整体需要区间查询+单点修改,容易发现树状数组就可以实现
点修改,子树修改,树链查询
因为有数链查询,我们考虑维护每个点 u 到根节点的权值和。这样侧重点就变成了考虑如何维护修改操作,然后查询操作就非常好维护了。
然后三个操作一起是不好考虑的,分成两个子问题考虑。(也就是考虑如何维护修改,使得查询时可以直接快速查询)
1.点修改,树链查询
修改一个点,这个点的所有儿子一定经过该点,于是单点修改变成子树修改,也就是区间修改。
然后链查询类比树上差分,单点查询即可。
2.子树修改,树链查询
类比上一个模型,推式子。对于子树 u 修改,就考虑子树 u 内的某个点 v 被如何修改即可。
改 v 相当于 1 的单点修改,一定是修改子树。那么容易发现 v 的父亲,v 的祖先一定会改到 v,也就是改 u 对 v 的贡献为:add*(dep[v]-dep[u]+1)。
然后拆式子变成:add*dep[v]-add*(dep[u]-1),发现 -add*(dep[u]-1) 是定值,可以直接修改。也就是对于 u 来说,只需要子树修改即可,也就是区间修改。
对于式子前半部分,再维护一颗树状数组就好,维护每次 add 的和,因为只有单点查询,最后取出来时 *dep[v] 即可。
整体只需要 区间修改+单点查询,可以树状数组、
鸽子
一些性质证明+例题。
有些还没来得及分类的题挂这:
CF708C
P5666
P1522
P1395
P3761
还有这份题单:图树模板 - 题单 - 洛谷 | 计算机科学教育新生态


 浙公网安备 33010602011771号
浙公网安备 33010602011771号