牛客 周赛105 20250829

牛客 周赛105 20250829

https://ac.nowcoder.com/acm/contest/115861

A：
题目大意：

void solve(){
	int k;
	cin>>k;
	cout<<1<<' '<<(1^k)<<endl;
}

签到

B：
题目大意：

void solve(){
	int n;
	cin>>n;
	vector<int> a(n+1);
	for (int i=1;i<=n;i++) cin>>a[i];
	int ans=0;
	for (int i=1;i<n;i++)
		ans=__gcd(ans,a[i]^a[i+1]);
	cout<<ans;
}

模拟一遍即可

C：
题目大意：

void solve(){
	int n,k;
	cin>>n>>k;
	if (k&1){cout<<-1;return;}
	k>>=1;
	for (int i=1;i<=n;i++){
		for (int j=1;j<=n;j++){
			if (i==j&&k){
				cout<<1;
				k--;
			}else cout<<0;			
		}
		cout<<endl;
	}
}

题目给定的 \(k\le 2n\) ，刚好符合每行每列的异或和全为 \(n\) 的情况

如果在矩阵 \((i,j)\) 的位置上放置一个 \(1\) ，那么第 \(i\) 行，第 \(j\) 列的异或和都会同时改变，换句话说某个位置上的 \(1\) 对答案的贡献要么为 \(0\) 要么为 \(\pm 2\)

所以当 \(k\) 为奇数时一定无解，有解时只在对角线上依次放 \(1\) 就能凑出答案

D：
题目大意：

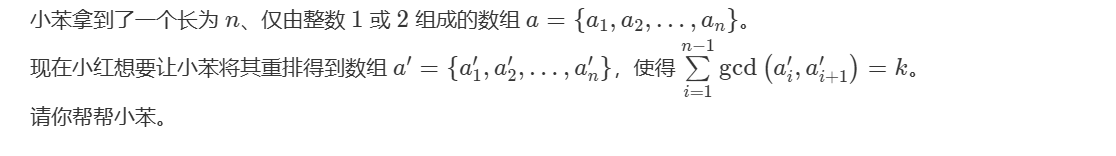
void solve(){
	int n,k;
	cin>>n>>k;
	int cnt[3]={0};
	for (int i=1;i<=n;i++) {
		int x;
		cin>>x;
		cnt[x]++;
	}
	int L;
	if (cnt[2]>cnt[1]) L=cnt[1]*2+2*(cnt[2]-cnt[1]-1);
	else L=n-1;
	int R=cnt[1]+2*(cnt[2]-1);
	if (k>R||k<L){cout<<-1;return;};
	vector<int> a(n+1);
	int idx=0;
	for (int i=1;i<=cnt[1];i++) a[++idx]=1;
	for (int i=1;i<=cnt[2];i++) a[++idx]=2;
	int i=1,j=cnt[1]+1;
	while (R>k){
		if (i<1||j>n) {cout<<-1;return;};
		swap(a[i],a[j]);
		i+=2,j+=1;
		R--;
	}
	for (int i=1;i<=n;i++) cout<<a[i]<<' ';
}

考虑排序可以形成的最大权值和最小权值：

• 最大权值，形如 \(111\cdots1222\cdots2\) ，前一段全 \(1\) 的权值为 \(cnt_1\) 后一段的权值为 \((cnt_2-1)\times 2\)

• 最小权值，形如 \(2121\cdots\) ，交错排列并且考虑 \(1,2\) 的数量

如果 \(k\) 在权值的范围内，那么一定可以通过重新排列达到，（存在改变权值 \(1\) 的操作）

\(111\cdots1222\cdots2\) ，交换其中某个 \(1,2\) 的位置变成 \(211\cdots 1212\cdots2\) 对答案的贡献为 \(-1\)

可以证明，通过不断的交换 \(1,2\) 的操作可以把序列从最大权值的排列变为最小权值的排列

int i=1,j=cnt[1]+1;
while (R>k){
	if (i<1||j>n) {cout<<-1;return;};
	swap(a[i],a[j]);
	i+=2,j+=1;
	R--;
}

E：
题目大意：

const int mod=998244353;

vector<int> e[200010];
LL a[200010];
int d[200010][35];

void solve(){
	int n,m;
	cin>>n>>m;
	for (int i=1;i<=n;i++) cin>>a[i];
	for (int i=1;i<=m;i++){
		int u,v;
		cin>>u>>v;
		e[u].push_back(v);
		e[v].push_back(u);
	}
	
	for (int i=1;i<=n;i++)
		for (int j=0;j<31;j++)
			d[i][j]=(a[i]>>j)&1;
	
	LL ans=0;
	for (int i=1;i<=n;i++){
		for (int j=0;j<31;j++){
			int cnt1=0,cnt0=0;
			for (auto v:e[i]){
				if ((a[i]>>j)&1){
					if (d[v][j]==0) ans+=cnt0*(1<<j);
					else ans+=cnt1*(1<<j);
				}else{
					if (d[v][j]==0) ans+=cnt1*(1<<j);
					else ans+=cnt0*(1<<j);
				}
				ans%=mod;
				if (d[v][j]==1) cnt1++;
				else cnt0++;
			}
		}
	}
	cout<<ans;
}

枚举每个顶点连接的两个邻居，暴力的最坏时间复杂度为 \(O(n^3)\) 级别

可以考虑通过二进制拆分，每个二进制位在计算异或时是相互独立的，所以枚举顶点后

再以 \(\log\) 的时间复杂度枚举所有的二进制位，每次遍历一遍所有的邻居记录下前缀 \(1,0\) 的数量

• 如果顶点当前的二进制位是 \(1\) ，那么异或产生贡献当且仅当两个邻居的二进制位都相同

  if ((a[i]>>j)&1){
  	if (d[v][j]==0) ans+=cnt0*(1<<j);//当前枚举的邻居为0时，产生的贡献为前缀0的数量
  	else ans+=cnt1*(1<<j);
  }
  

• 如果顶点当前的二进制位是 \(0\) ，那么异或产生贡献当且仅当两个邻居的二进制位都不同

  else{
  	if (d[v][j]==0) ans+=cnt1*(1<<j);
  	else ans+=cnt0*(1<<j);
  }
  

总时间复杂度为 \(O((n+m)\log N)\)

F：
题目大意：

void solve(){
	int n,m,t;
	cin>>n>>m>>t;
	struct node{int mg,ms,mk;};
	vector<vector<vector<int>>> dp(n+2,vector<vector<int>>(m+2,vector<int>(n*m+2)));
	vector<vector<vector<node>>> pre(n+2,vector<vector<node>>(m+2,vector<node>(n*m+2)));
	vector<int> ans;
	bool f=0;
	auto dfs=[&](auto &&self,int x,int pg,int sum){
		if (f) return;
		if (dp[x][pg][sum]) return;
		dp[x][pg][sum]=1;
		if (x>n){
			if (sum!=t) return;
			f=1;
			int G=pg,V=sum;
			for (int i=n+1;i>1;i--){
				auto [mg,ms,mk]=pre[i][G][V];
				ans.push_back(mk);
				G=mg,V=ms;
			}
			reverse(ans.begin(),ans.end());
			return;
		}
		
		for (int i=1;i<=m;i++){
			int g=__gcd(i,pg);
			if (!dp[x+1][g][sum+g]){
				pre[x+1][g][sum+g]={pg,sum,i};
				self(self,x+1,g,sum+g);
			}
		}
	};
	
	dfs(dfs,1,0,0);
	if (!f){cout<<-1<<endl;return;}
	for (auto i:ans) cout<<i<<' ';
	cout<<endl;
}

\(n,m=50\) 可以考虑 \(O(n^4)\) 级别的算法，想到用记忆化搜索和前导数组记录方案

\(dp_{i,j,k}\) 表示填了 \(i\) 位数，前缀 GCD 为 \(j\) ，总权值为 \(k\) 的状态是否可达

\(pre_{i,j,k}=\{mg,ms,mk\}\) 分别表示 \(dp_{i,j,k}\) 从前缀 GCD 为 \(mg\) ，总权值为 \(ms\) 且最后一位填 \(mk\) 的状态转移来的

到了递归出口时，如果总权值满足要求，那么通过 \(pre\) 数组回溯构造答案

int G=pg,V=sum;
for (int i=n+1;i>1;i--){
	auto [mg,ms,mk]=pre[i][G][V];
	ans.push_back(mk);
	G=mg,V=ms;
}