牛客 周赛104 20250825
牛客 周赛104 20250825
https://ac.nowcoder.com/acm/contest/114848
A:
题目大意:
void solve(){
int cnt=0;
for (int i=1;i<=4;i++){
int x;
cin>>x;
cnt+=(x==i);
}
cout<<cnt;
}
签到
B:
题目大意:

int n,k;
vector<int> ans;
bool vis[15];
bool dfs(int x){
if (x==n){
int cnt=0;
for (int i=0;i<n;i++) cnt+=(ans[i]==i+1);
return cnt==k;
}
for (int i=1;i<=n;i++){
if (vis[i]) continue;
vis[i]=1;
ans.push_back(i);
if (dfs(x+1)) return 1;
ans.pop_back();
vis[i]=0;
}
return 0;
}
void solve(){
cin>>n>>k;
if (dfs(0)) for (auto x:ans) cout<<x<<' ';
else cout<<-1;
}
DFS 枚举全排列,时间复杂度 \(O(2^n)\) ,\(n\le 10\) 时可以接受
C:
题目大意:

void solve(){
int n;
cin>>n;
unordered_map<int,int> mp;
for (int i=1;i<=2*n;i++){
int x;
cin>>x;
mp[x]++;
}
int ans=0;
for (auto [k,v]:mp)
if (k<=n) ans+=min(2,v);
cout<<ans;
}
将 \(2n\) 个数划分为两组,如果一个数是一个不动点,那么他一定满足 \(a_i=i\) ,所以可以先把这些数填入
剩余的数用来补在其他的位置上,由于只有两组,那么每个数所产生的贡献最多为 \(2\)
D:
题目大意:

int n,m;
int g[510][510];
int dfs(int x,int need){
int res=0;
for (int i=x;i<=n;i++){
if (g[i][x]==need) res=max(res,2);
if (g[i][x]!=x) res=max(res,1);
}
for (int j=x;j<=n;j++){
if (g[x][j]==need) res=max(res,2);
if (g[x][j]!=x) res=max(res,1);
}
return res;
}
void solve(){
cin>>n>>m;
for (int i=1;i<=n;i++)
for (int j=1;j<=m;j++)
cin>>g[i][j];
int cnt=0;
for (int i=1;i<=n;i++)
for (int j=1;j<=m;j++)
if (g[i][j]==min(i,j)) cnt++;
if (cnt==n*m) {cout<<cnt;return;};
int res=0;
for (int i=1;i<=n;i++){
for (int j=1;j<=m;j++){
if (g[i][j]!=min(i,j)){
res=max(res,dfs(g[i][j],min(i,j)));
if (res==2){
cout<<cnt+2;
return;
}
}
}
}
cout<<cnt+res;
}
暴力的想,枚举每一个不是矩阵不动点的点 \(a_{i,j}\) ,枚举另外一个要被交换的点 \(a_{x,y}\) , \(a_{i,j}=\mathrm{min}(x,y)\) 时贡献为 \(1\)
当同时满足 \(a_{x,y}=\mathrm{min}(i,j)\) 时对答案的贡献为 \(2\) ,这样的时间复杂度为 \(O(n^2m^2)\)
考虑枚举第二个点时可以优化,可以至少能使得 \(a_{i,j}\) 交换到 \((x,y)\) 后一定能产生贡献的位置 \((a_{i,j},a_{i,j}:n),(a_{i,j}:n,a_{i,j})\)
形如直拐角的一行和一列
1 1 1 1
1 2 2 2
1 2 3 3
1 2 3 4
在这些点上,如果存在一个不是矩阵不动点的点,那么贡献为 \(1\) ,同时如果交换后也能满足 \(a_{x,y}=\mathrm{min}(i,j)\) 那么贡献为 \(2\)
int dfs(int x,int need){
int res=0;
for (int i=x;i<=n;i++){
if (g[i][x]==need) res=max(res,2);
if (g[i][x]!=x) res=max(res,1);
}
for (int j=x;j<=n;j++){
if (g[x][j]==need) res=max(res,2);
if (g[x][j]!=x) res=max(res,1);
}
return res;
}
时间复杂度为 \(O(nm\times(n+m))\)
E:
题目大意:

int a[300010];
int pos[300010];
void solve(){
int n;
cin>>n;
for (int i=1;i<=n;i++) cin>>a[i];
for (int i=1;i<=n;i++) pos[a[i]]=i;
int L=1e9,R=0,l=1e9+1,r=-1;
LL ans=0;
for (int i=1;i<=n;i++){
L=min(L,pos[i]);
R=max(R,pos[i]);
LL t=1ll*(L)*(n-R+1);
ans+=1ll*t;
}
cout<<ans;
}
一个子数组中的不动点当且仅当这个不动点 \(a_i=i\) ,所以分开考虑每个元素可以带来的贡献
如果子数组中存在一个数为 \(i\) ,要想要这个数产生贡献,那么子数组中一定要有 \(i-1\) ,由此递推
所以考虑子数组中元素从 \(1\) 开始扩展,设区间 \([L,R]\) 是能满足区间内的数产生贡献的区间
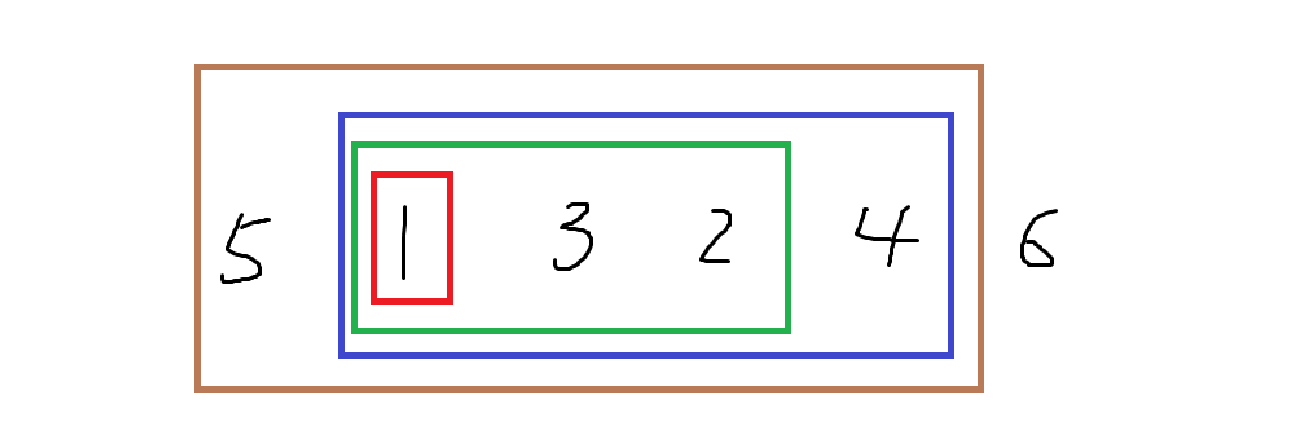
记录下每一个数在数组中的位置,然后维护区间的左右端点
从 \(1\) 开始扩展,要让数 \(i\) 产生贡献,那么 \(i\) 一定要在维护的区间内,区间外可以随意选数来构成子数组
左右各利用插板法可以得到贡献为 \(L\times (n-R+1)\)
F:
题目大意:

vector<int> e[200010];
int dep[200010],fa[200010][20];
void dfs(int x,int p){
dep[x]=dep[p]+1;
fa[x][0]=p;
for (int i=1;i<=18;i++)
fa[x][i]=fa[fa[x][i-1]][i-1];
for (auto v:e[x]){
if (v==p) continue;
dfs(v,x);
}
}
int lca(int x,int y){
if (dep[x]<dep[y]) swap(x,y);
for (int i=18;i>=0;i--)
if (dep[fa[x][i]]>=dep[y]) x=fa[x][i];
if (x==y) return y;
for (int i=18;i>=0;i--)
if (fa[x][i]!=fa[y][i])
x=fa[x][i],y=fa[y][i];
return fa[x][0];
}
void solve(){
int n;
cin>>n;
for (int i=1;i<n;i++){
int u,v;
cin>>u>>v;
e[u].push_back(v);
e[v].push_back(u);
}
dfs(n,0);
LL ans=0,P=1;
for (int i=1;i<=n;i++){
P=lca(i,P);
ans+=dep[P];
}
cout<<ans;
}
类似的想法,如果一个子树中 \(i\) 是一个不动点,那么 \(i-1\cdots 1\) 这些数也一定在这个子树中
所以从 \(1\) 开始扩展子树,维护子树的父亲节点,每次扩展的数 \(i\) 如果要产生贡献,那么就要将这个点加入集合中
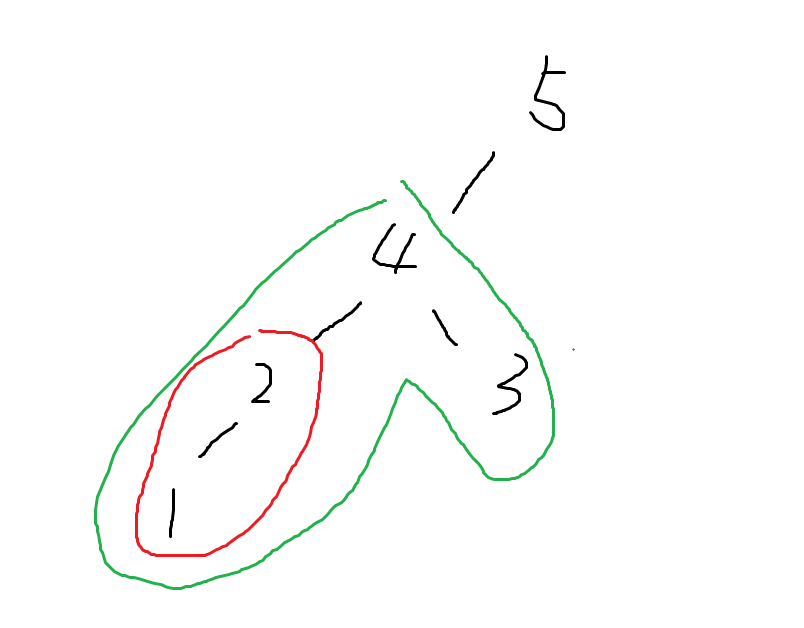
当图中 \(3\) 要能产生贡献时,必然和 \(1,2\) 在一个子树上,求出 \(3\) 和 \(1,2\) 集合的 LCA \(=4\) 后,合并这两个分支得到集合 \(1,2,3,4\)
从 \(4\) 到根节点上所有的数都可以任选,那么产生的贡献为 \(dep_4=2\)
推广到其他情况同理



 浙公网安备 33010602011771号
浙公网安备 33010602011771号