牛客 周赛103 20250821
牛客 周赛103 20250821
https://ac.nowcoder.com/acm/contest/114593
A:
题目大意:
void solve(){
string s;
cin>>s;
if (s.back()=='0') cout<<"NO";
else cout<<"YES";
}
签到
B:
题目大意:

void solve(){
int n;
cin>>n;
vector<int> a(n);
for (auto &x:a) cin>>x;
int p;
for (p=0;p<n-1;p++)
if (a[p]>a[p+1]) break;
if (p+1==n||(is_sorted(a.begin()+p+1,a.end())&&a[n-1]<=a[0])) cout<<"YES"<<'\n';
else cout<<"NO"<<'\n';
}
循环数组满足单调不减,一定可以找到一个最小的起点
起点要么是数组的开头元素,要么是第一个不满足 \(a_{i+1}\ge a_i\) 的元素
如果是第二种情况,那么将数组从下标 \(i\) 开始,判断 \([i,n]\) 区间内的元素是否单调不减并且 \(a_n\le a_1\) (拼接后仍然不减)
bool is_sorted (ForwardIterator first, ForwardIterator last, Compare comp);
函数判断从迭代器 first 到迭代器 last 之间的元素是否满足比较函数 comp (默认单调不减)
C:
题目大意:

const int mod=1e9+7;
LL ksm(LL a,LL b,LL p){
LL res=1;
while (b){
if (b&1) res=res*a%p;
a=a*a%p;
b>>=1;
}
return res;
}
void solve(){
int n;
cin>>n;
cout<<ksm(2,n-1,mod)<<endl;
}
考虑一个区间和他的子区间是否是一个排列,从小到大看
长度为 \(1\) 的排列满足题意的有 \(\{1\}\) 一种,长度为 \(2\) 的排列满足题意的有 \(\{1,2\},\{2,1\}\)
长度为 \(3\) 的排列满足题意的有 \(\{1,2,3\},\{3,1,2\},\{2,1,3\},\{3,2,1\}\)
每次扩展一个元素进来必然是在左右的两端加入,那么对于每一个加入的元素都有两种选择
所以对于一个长 \(n\) 的排列,满足题意的排列个数有 \(2^{n}\) 个
D:
题目大意:

void solve(){
int n;
cin>>n;
string s;
cin>>s;
int cnt=0;
for (int i=0;i<n-1;i++){
if ((s[i]!=s[i+1])||(s[i]!=s[i+1])) cnt++;
}
if (cnt>=3){
cout<<0<<'\n';
return;
}
if (cnt==0){
cout<<2<<'\n';
return;
}
if (cnt==1){
for (int i=0;i<n-2;i++){
if (s[i]==s[i+1]&&s[i+1]==s[i+2]){
cout<<1<<'\n';
return ;
}
}
cout<<2<<'\n';
return;
}
if (s[0]!=s[1]&&s[n-1]!=s[n-2] && n==4) cout<<2<<'\n';
else cout<<1<<'\n';
}
首先考虑一下修改一个字符可以产生的贡献:
- 操作一:如果这个字符是在一段长为 \(3\) 的全相同子串上比如 \(111,000\),修改中间的字符后可以产生 \(2\) 的贡献
- 操作二:如果这个字符和一个与他不同的字符相邻比如 \(01,10\) ,修改左侧的字符不产生贡献
- 操作三:如果这个字符处于开头或结尾且和相邻字符相同比如 \(\#00,11\#\) 修改一个字符会产生 \(1\) 的贡献
读入原有的字符串,如果 \(01,10\) 串的个数已经大于等于 \(3\) ,那么显然不需要修改
-
如果 \(cnt=0\) ,原字符串肯定为全 \(1\) 或者全 \(0\) ,此时修改任意两个不相邻的字符即可使得 \(cnt\ge 3\)
-
如果 \(cnt=1\) ,判断第一个操作是否存在,可以直接产生 \(2\) 的贡献,否则需要修改两个字符
-
如果 \(cnt=2\) ,那么原字符串一定形如两个全相同的 \(1/0\) 串夹一段全相同的 \(0/1\) 串
我们一定可以通过第一个操作或者第三个操作满足条件,除非原字符串为 \(0110,1001\) (修改两次)
E:
题目大意:

vector<int> e[100010];
int a[100010];
int fa[100010];
int st[1<<21+1];
void dfs(int x,int p){
fa[x]=p;
for (auto v:e[x]){
if (v==p) continue;
dfs(v,x);
}
int s1=0,s2=0;
int step=0;
int now=x;
while (step<=21&&now!=0){
s1=(s1<<1)|a[now];
s2=s2|(a[now]<<step);
st[s1]++,st[s2]++;
step++;
now=fa[now];
}
}
void solve(){
int n,q;
cin>>n>>q;
string s;
cin>>s;
for (int i=0;i<n;i++) a[i+1]=(s[i]=='1');
for (int i=1;i<n;i++){
int u,v;
cin>>u>>v;
e[u].push_back(v);
e[v].push_back(u);
}
dfs(1,0);
while (q--){
int x;
cin>>x;
if (st[x]) cout<<"YES"<<'\n';
else cout<<"NO"<<'\n';
}
}
询问的 \(x\) 小于 \(2^{20}\) ,那么对于一个路径对答案有效的最长长度就是 \(21\) 个节点,可以对每一个节点都维护出以它为端点向上和向下 \(20\) 个节点的路径,并处理这些路径上形成的二进制串,时间复杂度为 \(O(21n)\)
维护路径是,一条路径有两个端点,我们只需要对一个端点进行单向处理就能维护出这一整条路径
int s1=0,s2=0;//从两个端点走完整个路径的二进制串
int step=0;//节点个数
int now=x;//当前的节点
while (step<=21&&now!=0){
s1=(s1<<1)|a[now];//新访问到的节点添加在末尾
s2=s2|(a[now]<<step);//新访问到的节点添加在开头
st[s1]++,st[s2]++;//记录下二进制串对应的十进制表示
step++;
now=fa[now];
}
记录下所有可以被表示的十进制整数,空间复杂度 \(O(2^{21})\) 在允许的范围内可以存下
最后对每一个询问进行 \(O(1)\) 回答
F:
题目大意:

using u128=unsigned __int128;
const ULL base=13331;
const ULL mod=212370440130137957;
void solve(){
int n,m;
string S;
cin>>n>>m>>S;
vector<string> a(m);
for (int i=0;i<m;i++) cin>>a[i];
int slen=0;
for (int i=0;i<m;i++) slen+=a[i].size();
vector<vector<int>> tr(slen+10,vector<int>(26,0)),cnt(slen+10,vector<int>(26,0));
int idx=0;
auto insert=[&](string s)->void{
int p=0,len=s.size();
for (int i=0;i<len;i++){
int c=s[i]-'a';
if (tr[p][c]==0) tr[p][c]=++idx;
p=tr[p][c];
cnt[p][c]++;
}
};
for (int i=0;i<m;i++) insert(a[i]);
unordered_map<ULL,int> mp;
auto dfs=[&](auto &&self,int x,ULL hash,int sum)->void{
if (x>0) mp[hash]=sum;
for (int i=0;i<26;i++){
if (tr[x][i]==0) continue;
ULL nhash=((u128)hash*base+i+'a')%mod;
self(self,tr[x][i],nhash,sum+cnt[tr[x][i]][i]);
}
};
dfs(dfs,0,0,0);
S=' '+S;
vector<ULL> f(n+1,0),g(n+1,0);
g[0]=1;
for (int i=1;i<=n;i++){
f[i]=((u128)f[i-1]*base+S[i])%mod;
g[i]=(u128)g[i-1]*base%mod;
}
auto get_hash=[&](int l,int r)->ULL{
int len=r-l+1;
ULL ans=(f[r]-(u128)f[l-1]*g[len]%mod+mod)%mod;
return ans;
};
int ans=0;
for (int i=1;i<=n;i++){
int l=i,r=n+1;
while (l+1!=r){
int mid=l+r>>1;
ULL res=get_hash(i,mid);
if (mp.count(res)) l=mid;
else r=mid;
}
ULL res=get_hash(i,l);
if (mp.count(res)) ans=max(ans,mp[res]);
}
cout<<ans<<'\n';
}
处理所有的字符串集合 \(t\) 中每个字符串的最长公共前缀可以利用 tire 树记录,插入一个字符串串时对所在路径上的节点都记录下相同前缀的个数,例如字符串集合 \(\{abc,abc,adb\}\)
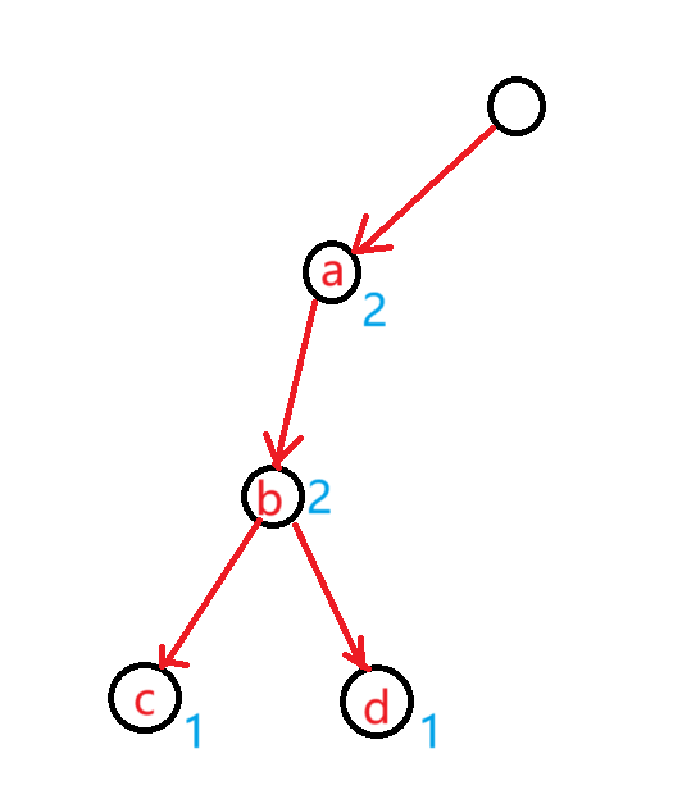
可以清晰看出在集合 \(t\) 内部 \(ab\) 的最长公共前缀为 \(2+2=4\) 个字符,\(abc\) 的最长公共前缀为 \(2+2+1\) 个字符
然后问题转化为怎么把 \(s\) 中去掉某个前缀串后的字符串映射到 tire 树上计算最长公共前缀
对整棵 tire 树进行一遍DFS,对每一个公共前缀串都进行一次字符串哈希,同时映射对应的最长公共前缀
unordered_map<ULL,int> mp;
auto dfs=[&](auto &&self,int x,ULL hash,int sum)->void{
if (x>0) mp[hash]=sum;
for (int i=0;i<26;i++){
if (tr[x][i]==0) continue;
ULL nhash=((u128)hash*base+i+'a')%mod;
self(self,tr[x][i],nhash,sum+cnt[tr[x][i]][i]);
}
};
dfs(dfs,0,0,0);
暴力的想,枚举 \(s\) 删掉前缀串的终点然后遍历剩下的后缀串记录最长公共前缀,时间复杂度是 \(O(\lvert s\rvert ^2)\)
可以发现遍历后缀串时计算的最长公共前缀是满足单调性的,形象化的说:
如果 \(S\) 的某个前缀串 \(L=s_1s_2\cdots s_i\) 与匹配串 \(T\) 的最长公共前缀长度为 \(x\),那么前缀串 \(L^\prime=s_1s_2\cdots s_is_{i+1}\) 和匹配串 \(T\) 的最长公共前缀长度 \(y\) 一定不小于 \(x\)
所以枚举\(s\) 删掉前缀串的终点 \(i\) 后,二分查找后缀串中的某个特定位置 \(p\) ,满足 \(s_{[i:p]}\) 在 tire 树中,而\(s_{[i:p+1]}\) 则不在
此时 \(s_{[i:p]}\) 哈希后映射的整数就是 \(s\) 从 \(i\) 开始的后缀串与集合 \(t\) 中每个字符串的最长公共前缀之和
for (int i=1;i<=n;i++){
int l=i,r=n+1;
while (l+1!=r){
int mid=l+r>>1;
ULL res=get_hash(i,mid);
if (mp.count(res)) l=mid;
else r=mid;
}
ULL res=get_hash(i,l);
if (mp.count(res)) ans=max(ans,mp[res]);
}
时间复杂度可以被优化到 \(O(\lvert s\rvert \log\lvert s\rvert)\) ,同时对于字符串 \(s_{[i,p]}\) 的哈希也必须进行 \(O(1)\) 计算
标准的字符串区间哈希操作
S=' '+S;//下标从1开始
vector<ULL> f(n+1,0),g(n+1,0);
g[0]=1;
for (int i=1;i<=n;i++){
f[i]=((u128)f[i-1]*base+S[i])%mod;
g[i]=(u128)g[i-1]*base%mod;
}
auto get_hash=[&](int l,int r)->ULL{
int len=r-l+1;
ULL ans=(f[r]-(u128)f[l-1]*g[len]%mod+mod)%mod;
return ans;
};



 浙公网安备 33010602011771号
浙公网安备 33010602011771号