牛客2025多校 R5
牛客2025多校 R5
I:
题目大意:

void solve(){
LL n;
cin>>n;
LL s=(n+1)*n/2;
LL ans=9e18;
for (LL i=1;i*i<=s;i++)
if (s%i==0&&(i>=n||s/i>=n))
ans=min(ans,2LL*(i+s/i));
cout<<ans;
}
可以计算出总面积为 \(n(n+1)/2\) ,题目的约束下一点存在合适的矩形可以被构造出来,那么矩形的长宽为 \(a,b\)
枚举合适的 \(a\cdot b=S=n(n+1)/2\) 得到答案,时间复杂度为 \(O(n)\) ,特别的 \(a,b\) 必须满足的条件是都要大于等于 \(n\) ,即不能比最长的矩形还要小
E:
题目大意:

int a[100010];
int d[100010][32];
int pre[100010][32];
int x[32][4];
void solve(){
int n;
cin>>n;
for (int i=1;i<=n;i++) cin>>a[i];
for (int i=1;i<=n;i++){
int x=a[i],idx=0;
while (x){
d[i][++idx]=(x&1);
x>>=1;
}
}
for (int i=1;i<=n;i++)
for (int j=1;j<=30;j++)
pre[i][j]=pre[i][j-1]^d[i][j];
LL ans=0;
for (int i=1;i<=30;i++){
for (int j=1;j<=n;j++){
if (pre[j][i]==0&&d[j][i]==0) x[i][0]++;
if (pre[j][i]==0&&d[j][i]==1) x[i][1]++;
if (pre[j][i]==1&&d[j][i]==0) x[i][2]++;
if (pre[j][i]==1&&d[j][i]==1) x[i][3]++;
}
ans+=1ll*(x[i][0]*x[i][3]+x[i][2]*x[i][1])*(1<<(i-1));
}
cout<<ans;
}
考虑每一位的贡献问题,当 \(a\oplus_m b\) 的结果在某一位上为 \(1\) 时,\(a,b\) 在这一位上会被约束
明显的有如果异或后这一位为 \(1\) ,那么 \(a,b\) 在这一位上一定不会相同,现在考虑这一位之前异或结果为 \(1\) 的数量
如果 \(a\) 的这一位为 \(1\) 且这是第奇数个 \(1\) ,那么只有当 \(b\) 的这一位为 \(0\) 且已经有了奇数个 \(1\) 才能产生贡献
简单证明:
设 \(a\) 的这一位是第 \(x\) 个 \(1\) ,那么之前就有 \(x-1\) 个 \(1\) ,\(b\) 的这一位之前有 \(y\) 个 \(1\),共有 \(m\) 位
那么普通异或的结果是这一位之前有 \(\mathrm{min}(m-(x-1),y)+\mathrm{min}(m-y,(x-1))\) 个 \(1\) ,可以发现如果取 \(\mathrm{min}(m-(x-1),y)=y\) 时必有 \(\mathrm{min}(m-y,(x-1))=(x-1)\) ,所以普通异或后的结果在这一位之前有 \(2m-x-y+1\) 或 \(x+y-1\) 个 \(1\)
当且仅当 \(x,y\) 的奇偶性不同时才能保证这一位异或后的 \(1\) 是第奇数个
ans+=1ll*(x[i][0]*x[i][3]+x[i][2]*x[i][1])*(1<<(i-1));
最后单独计算每一位的贡献求和后得到答案
J:
题目大意:

int n,m;
vector<vector<int>> g;
vector<vector<int>> dis;
vector<vector<bool>> vis;
vector<pair<int,int>> zro;
int dx[]={0,0,-1,1};
int dy[]={1,-1,0,0};
bool judge(int T){
int umin=-Iinf,umax=Iinf,vmin=-Iinf,vmax=Iinf;
bool f=0;
for(auto [x,y]:zro){
if(dis[x][y]>T){
f=1;
int u=x+y,v=x-y;
umin=max(umin,u-T);
umax=min(umax,u+T);
vmin=max(vmin,v-T);
vmax=min(vmax,v+T);
}
}
if(!f)return 1;
if(umin>umax||vmin>vmax)return 0;
for(auto [x,y]:zro){
int u=x+y,v=x-y;
if(u>=umin&&u<=umax&&v>=vmin&&v<=vmax)return 1;
}
return 0;
}
void solve(){
cin>>n>>m;
g.assign(n+1,vector<int>(m+1,0));
dis.assign(n+1,vector<int>(m+1,1e9));
vis.assign(n+1,vector<bool>(m+1,0));
for (int i=1;i<=n;i++)
for (int j=1;j<=m;j++)
cin>>g[i][j];
queue<pair<int,int>> q;
for (int i=1;i<=n;i++){
for (int j=1;j<=m;j++){
if (g[i][j]==1){
dis[i][j]=0;
q.push({i,j});
vis[i][j]=1;
}
else
zro.push_back({i,j});
}
}
while (q.size()){
auto t=q.front();
q.pop();
for (int i=0;i<4;i++){
int tx=t.first+dx[i],ty=t.second+dy[i];
if (tx<1||ty<1||tx>n||ty>m) continue;
if (vis[tx][ty]==1) continue;
vis[tx][ty]=1;
q.push({tx,ty});
dis[tx][ty]=dis[t.first][t.second]+1;
}
}
int l=-1,r=2e5+1;
while (l+1!=r){
int mid=l+r>>1;
if (judge(mid)) r=mid;
else l=mid;
}
cout<<r<<endl;
}
首先对每一个白色点都预处理出它被染成黑色的时间 \(dis_{i,j}\) ,然后二分时间找是否能满足所有点都被变为黑色
当在时间 \(T\) 内所有点都能被染成黑色,说明所有的 \(dis_{i,j}>T\) 的点都要通过我们手动染色的点被染黑
取所有 \(dis_{i,j}>T\) 的点根据 \(T\) 时间形成的区域(区域内所有点到 \((i,j)\) 这个点的距离都小于 \(T\) ),我们就说如果点 \((i,j)\) 能被染成黑色,当且仅当这个区域内存在我们手动染色的点
对所有区域取交集后,在交集内的白色的点即为可以将所有 \(dis_{i,j}>T\) 的点都染上黑色的点,如果不存在这样的点说明 \(T\) 取的比较小
如果能够取到这样的点,那么就缩小 \(T\) 直到一个确定的值
这样的区域是一个曼哈顿圆,即 \(\lvert u-x\rvert+\lvert v-y\rvert\le T\) ,更改参考系为 \((x-y),(x+y)\)
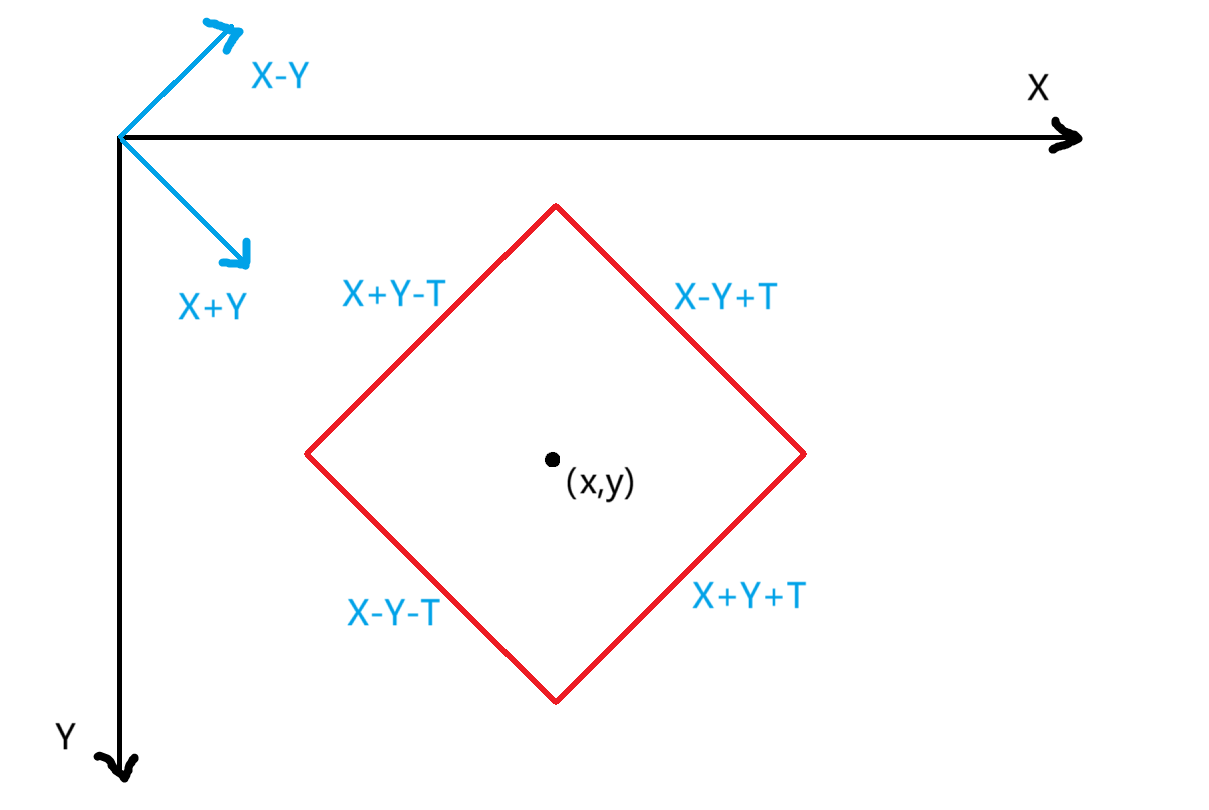
维护曼哈顿圆在映射坐标系下的交集即可
for(auto [x,y]:zro){
if(dis[x][y]>T){
f=1;
int u=x+y,v=x-y;
umin=max(umin,u-T);
umax=min(umax,u+T);
vmin=max(vmin,v-T);
vmax=min(vmax,v+T);
}
}
K:
题目大意:

const int mod=998244353;
LL fac[110];
vector<int> e[200010];
vector<pair<int,int>> path;
int p[200010],x[30];
int fa[200010][20],pre[200010],dep[200010],idx;
LL A[1<<23],B[1<<23],ans;
int n,m,k;
LL ksm(LL a,LL b,LL p){
LL res=1;
while (b){
if (b&1) res=res*a%mod;
a=a*a%mod;
b>>=1;
}
return res;
}
void dfs(int x,int p){
pre[x]=p;
dep[x]=dep[p]+1;
fa[x][0]=p;
for (auto v:e[x]){
if (v==p) continue;
dfs(v,x);
}
}
int lca(int a,int b){
if (dep[a]<dep[b]) swap(a,b);
for (int i=18;i>=0;i--){
if (dep[fa[a][i]]>=dep[b])
a=fa[a][i];
}
if (a==b) return b;
for (int i=18;i>=0;i--){
if (fa[a][i]!=fa[b][i])
a=fa[a][i],b=fa[b][i];
}
return fa[a][0];
}
void FWT(LL a[],int op){
for (int d=2;d<=(1<<m);d<<=1){
int k=d>>1;
for (int i=0;i<(1<<m);i+=d){
for (int j=0;j<k;j++){
(a[i+j+k]+=a[i+j]*op+mod)%=mod;
}
}
}
}
bool judge(int mid){
for (int i=0;i<(1<<m);i++)
B[i]=ksm(A[i],mid,mod);
LL sum=0;
for (int i=0;i<(1<<m);i++){
if (__builtin_popcount((1<<m)-i-1)&1) sum-=B[i];
else sum+=B[i];
sum=(sum+mod)%mod;
}
if (sum!=0) ans=sum;
return sum==0;
}
void solve(){
fac[0]=1;
for (int i=1;i<=100;i++) fac[i]=fac[i-1]*i%mod;
cin>>n>>m>>k;
path.resize(n+1);
for (int i=1;i<n;i++){
int u,v;
cin>>u>>v;
e[u].push_back(v);
e[v].push_back(u);
path[i]={u,v};
}
dfs(1,0);
for (int i=1;i<=m;i++) cin>>x[i];
for (int i=1;i<n;i++)
if (pre[path[i].first]==path[i].second)
swap(path[i].second,path[i].first);
for (int i=1;i<=18;i++)
for (int j=1;j<=n;j++)
fa[j][i]=fa[fa[j][i-1]][i-1];
int road=0;
while (k--){
int a,b;
cin>>a>>b;
int c=lca(a,b);
int mask=0;
for (int i=1;i<=m;i++){
if (lca(path[x[i]].first,c)==c){
if (lca(path[x[i]].second,a)==path[x[i]].second||
lca(path[x[i]].second,b)==path[x[i]].second)
mask|=1<<(i-1);
}
}
road|=mask;
A[mask]++;
}
if (road!=(1<<m)-1){
cout<<-1<<endl;
return;
}
if (A[(1<<m)-1]){
cout<<1<<' '<<A[(1<<m)-1]<<endl;
return;
}
FWT(A,1);
int l=0,r=m+2;
while (l+1!=r){
int mid=l+r>>1;
if (judge(mid)) l=mid;
else r=mid;
}
cout<<r<<' '<<ans*ksm(fac[r],mod-2,mod)%mod;
}
给出的道路是无序的,因为我们在一棵树上寻找答案,所以首先需要对树边进行处理,即 \(path_i=(u_i,v_i)\) 表示 \(i\) 时一条从 \(u_i\) 到 \(v_i\) 的树边,且 \(u_i\) 是上层的节点
然后对每对给出的旅游线路都处理出这条线路上被经过的特定道路,具体流程是:
给定的旅游线路起点终点分别为 \((a,b)\) ,LCA 处理出他们的最近祖先,枚举所有的特定道路
当且仅当存在一条特定道路它的 \(u_i\) 的层数小于 LCA 的层数,且 \(v_i\) 是 \((a,b)\) 任意一个的祖先,\((u_i,v_i)\) 就被 \((a,b)\) 经过
然后是集合计数问题,我们需要找到能够覆盖完所有特定道路的旅游线路集合
类似于集合并集的关系,考虑构造多项式 \(A=a_0+a_1x+\cdots+a_nx^n\) ,其中 \(a_i\) 表示能够通过二进制表示下的 \(i\) 的了旅游线路的条数
例如:\(a_4=4\) 表示能够通过 \(i=100_2\) 即第 \(3\) 条特定道路的旅游线路数
利用 FWT 处理多项式 \(A\) ,考虑二分答案最少旅游线路数
bool judge(int mid){
for (int i=0;i<(1<<m);i++)
B[i]=ksm(A[i],mid,mod);
LL sum=0;
for (int i=0;i<(1<<m);i++){
if (__builtin_popcount((1<<m)-i-1)&1) sum-=B[i];
else sum+=B[i];
sum=(sum+mod)%mod;
}
if (sum!=0) ans=sum;
return sum==0;
}
多项式 \(B=A^{mid}\) 即 \(mid\) 条旅游线路能够覆盖的特定道路的集合,\(b_i\) 表示在 \(mid\) 条旅游线路的覆盖下,经过二进制表示下 \(i\) 的方案数
例如:\(b_5=7\) 表示能够通过 \(i=101_2\) 即能够覆盖第 \(1,3\) 条特定道路的方案数
设最后二分出来的最少旅游条数为 \(x\) ,方案数即为 \(b_{2^m-1}/x!\) ,除掉阶乘的原因是在 FWT 中同一个划分会被计算 \(x\) 次,由于我们的方案不能重复,所以需要去掉重复的划分的数量 \(x!\)
又因为每轮二分的 FWT 都会调用一次逆变换,时间复杂度最坏为 \(O(m^22^m)\) ,事实上我们不需要通过逆变换计算出多项式 \(B\) 的每一项的系数,采用容斥原理可以在 \(2^m\) 的时间复杂度内求得任意一项的系数
所以总时间复杂度可以优化为 \(O(m2^m)\)
H:
题目大意:



int n,m,s,t;
int a[110],q[110],b[110],c[110],pre[110];
int dp[110][110][110];
bool judge(int p){
memset(dp,-0x3f,sizeof dp);
dp[0][0][0]=0;
for (int i=0;i<=n;i++){
for (int j=0;j<=t;j++){
for (int k=0;k<=j;k++){
if (dp[i][j][k]>=s) return 1;
int sum=pre[i];
if (j<t)
dp[i][j+1][k+1]=max(dp[i][j+1][k+1],dp[i][j][k]+sum);
if (i+1<=n){
int d=(a[i+1]-1)/sum+1;
if (j+d<=t)
dp[i+1][j+d][k+d]=max(dp[i+1][j+d][k+d],dp[i][j][k]);
d=(a[i+1]-c[i+1]-1)/sum+1;
if (p==0) continue;
int u=(b[i+1]-1)/p+1;
if (j+d<=t&&k-u+d>=0)
dp[i+1][j+d][k-u+d]=max(dp[i+1][j+d][k-u+d],dp[i][j][k]);
}
}
}
}
return 0;
}
void solve(){
cin>>m>>s>>t>>n;
for (int i=1;i<=n;i++) cin>>a[i]>>q[i]>>b[i]>>c[i];
pre[0]=m;
for (int i=1;i<=n;i++) pre[i]=pre[i-1]+q[i];
int l=-1,r=10001;
while (l+1!=r){
int mid=l+r>>1;
if (judge(mid)) r=mid;
else l=mid;
}
if (r==10001) cout<<-1;
else cout<<r;
}
二分最小的生产力 \(p\) ,对于每一个 \(p\) 我们都进行一次动态规划判断是否存在这样的一个最优方案使得在 \(t\) 天内可以将科技点胜利槽叠加到 \(s\) 点
定义 \(dp_{i,j,k}\) 表示解锁了前 \(i\) 个科技,当前为第 \(j\) 天,剩余 \(k\) 天的生产力没有分配时可以得到的最大科技胜利点
对于任意一天 \(j\) ,我们有以下的转移方向:\(sum_i\) 表示解锁第 \(i\) 个科技后每回合可以得到的科技点
-
不解锁下一项科技,那么有 \(dp_{i,j,k}+sum_i\to dp_{i,j+1,k+1}\)
-
解锁下一项科技不使用尤里卡,\(dp_{i,j,k}\to dp_{i+1,j+d,k+d}\),\(d\) 表示解锁下一项科技不使用尤里卡时所需要投入的科技点的天数,因为在这一段时间内,我们都不分配生产力,所以待分配的生产力的天数多增加 \(d\)
-
解锁下一项科技使用尤里卡,\(dp_{i,j,k}\to dp_{i+1,j+d,k+d-u}\) ,\(u\) 表示解锁下一项科技所需要投入的尤里卡所需的天数,\(d\) 表示解锁下一项科技使用尤里卡时所需要投入的科技点的天数,这一段时间内,我们会度过 \(d\) 天,会消耗 \(u\) 天来分配生产力,所以待分配生产力的天数为 \(k+d-u\)
A:
题目大意:

void solve(){
int n,k,s,t;
cin>>n>>k>>s>>t;
if (s==t){
cout<<0<<endl;
return;
}
if (n==k){
if (s+t==n) cout<<1<<endl;
else cout<<-1<<endl;
return;
}
int L=2*min(n-k,k);
int sl=s+k-2*min(s,k);
int sr=s+k-2*max(0,k-n+s);
int ans=2e9;
if (s%2==t%2) ans=min(ans,2*((abs(t-s)-1)/L+1));
if (sl%2==t%2){
if (t<sl) ans=min(ans,1+2*((sl-t-1)/L+1));
if (t>sr) ans=min(ans,1+2*((t-sr-1)/L+1));
if (t>=sl&&t<=sr) ans=min(ans,1);
}
if (ans==2e9) cout<<-1<<endl;
else cout<<ans<<endl;
}
考虑连续两次操作带来的影响:如果第一次改变 \(k\) 枚,第二次也改变 \(k\) 枚,设在这两次中都改变的硬币个数为 \(l\)
那么总的改变硬币个数为 \(2k-2l\) ,必然是偶数个,所以可以递推地得到:
- 连续两次操作可以改变 \(0\) 枚硬币
- 连续两次操作可以改变 \(2\) 枚硬币,当 \(k\in [1,n-1]\) 时
- …………
可以得到连续两次操作可以改变 \(0,2,\cdots ,2\times\mathrm{min}(n-k,k)\) 枚硬币,证明:
设两次操作后只改变一次状态的硬币个数为 \(2a\) ,则有 \(k-a\) 枚硬币在两次操作后的状态不变
\(2a+k-a\le n\) 这是一定满足的必要条件(至少有 \(2a+k-a\) 枚不同的硬币才能选到)
得到 \(a\le n-k\) 又因为 \(a\in [0,k]\) ,所以 \(a\) 的取值范围为 \([0,\mathrm{min}(n-k,k)]\)
所以可以通过 \(2m,m\in N^+\) 次操作改变至多 \(m\times2\times\mathrm{min}(n-k,k)\) 枚硬币,那么当且仅当 \(s,t\) 的奇偶性相同时,我们才能通过这类操作使得硬币序列满足题意
int L=2*min(n-k,k);
if (s%2==t%2) ans=min(ans,2*((abs(t-s)-1)/L+1));
考虑奇数次操作可以带来的影响,可以看作先做一次单独的操作再做上述的偶数次操作,所以计算这一次单独操作的贡献
设这一次操作将朝上的硬币数量减少 \(i\),那么最终会有 \(s-i+(k-i)=s+k-2i\) 枚硬币朝上
满足的约束有:\(i\in[0,\mathrm{min}(s,k)],k-i\in[0,\mathrm{min}(k,n-s)]\) ,所以 \(i\in[\mathrm{max}(0,k-n+s),\mathrm{min}(s,k)]\)
做一次单独的操作可以将朝上的硬币个数变为 \([s+k-2\times\mathrm{max}(0,k-n+s),s+k-2\times\mathrm{min}(s,k)]\)
分类讨论 \(t\) 在区间上的取值:\(s_l=\mathrm{max}[0,s+k-2\times\mathrm{max}(0,k-n+s)],s_r=\mathrm{min}[n,s+k-2\times\mathrm{min}(s,k)]\)
- \(t\in [s_l,s_r]\) ,显然只需要一次操作就能满足题意
- \(t\in[0,s_l]\) ,通过一次操作将朝上的硬币个数变为 \(s_l\) ,然后做上述的偶数次操作
- \(t\in [s_r,n]\) ,同理
同样的需要在 \(s_l,s_r\) 和 \(t\) 的奇偶性相同时才能做之前的偶数次操作
if (sl%2==t%2){
if (t<sl) ans=min(ans,1+2*((sl-t-1)/L+1));
if (t>sr) ans=min(ans,1+2*((t-sr-1)/L+1));
if (t>=sl&&t<=sr) ans=min(ans,1);
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号