FFT 快速傅里叶变换

FFT 快速傅里叶变换

高效实现 DFT 离散傅里叶变换的一种手段，可以将两个 \(n\) 次多项式相乘的时间复杂度优化到 \(O(n\log n)\) 的算法

引理：给定 \(n\) 个点可以确定 \(n-1\) 次函数曲线的系数和系数存在映射关系

设两个多项式分别为 \(F(x),G(x)\)

  • 通过这两个多项式的系数经过系数乘法可以计算出 \(F(x)\cdot G(x)\) 的系数，基于单位圆划分出 \(n\) 个点，通过计算得到的这 \(n\) 个点值，我们就能唯一确定函数 \(F(x)\cdot G(x)\)

  • 基于单位圆划分出 \(n\) 个点，计算这两个多项式的这 \(n\) 个点值，再利用点值乘法确定函数 \(F(x)\cdot G(x)\)

单位圆

image-20250807220538390

复平面的单位元圆上的点都可以被表示为：

\[z=\cos \theta +i\sin \theta\ (0\le \theta < 2\pi) \]

把单元圆 \(n\) 等分（\(n=2^{b\in N^+}\)），可以得到方程 \(z^n=1\) 的 \(n\) 个复数根 \(\omega_n\) ，单位根为：

\[\omega_n^k=\cos \frac{2\pi k}{n}+i\sin\frac{2\pi k}{n} \]

满足性质有：\(\omega _n^k\cdot \omega_n^m=\omega_n^{k+m},(\omega _n^k)^m=\omega _n^{km}\) ，周期性：\(\omega _n^{k+n}=\omega _n^k\) ，对称性：\(\omega _n^{k+\frac{n}{2}}=-\omega _n^k\) ，折半性：\(\omega _n^{2k}=\omega _{\frac{n}{2}}^k\)

正变换

通过多项式 \(A(x)\) 的系数求点值，设系数为 \(a_0,a_1,\cdots,a_{n-1}\) ，则 \(A(x)\) 被表示为：

\[A(x)=a_0+a_1x+a_2x^2+\cdots +a_{n-1} x^{n-1} \]

将奇次项和偶次项分离后有：

\[A(x)=(a_0+a_2x^2+\cdots +a_{n-2}x^{n-2})+(a_1+a_3x^2+\cdots+a_{n-1}x^{n-2})x \]

分别设 \(A_0(x),A_1(x)\) 为：

\[A_0(x)=a_0+a_2x+a_4x^2+\cdots+a_{n-2}x^{\frac{n}{2}-1}\\ A_1(x)=a_1+a_3x+a_5x^2+\cdots+a_{n-1}x^{\frac{n}{2}-1}\\ A(x)=A_0(x^2)+A_1(x^2)x \]

将 $$x=\omega _n^k\ (k<\frac{n}{2})$$ 代入得：

\[A(\omega_n^k)=A_0(\omega_n^{2k})+A_1(\omega_n^{2k})\omega_n^k=A_0(\omega_\frac{n}{2}^{k})+A_1(\omega_\frac{n}{2}^{k})\omega_n^k \]

同理代入 $$x=\omega _n^{k+\frac{n}{2}}\ (k<\frac{n}{2})$$

\[A(\omega_n^{k+\frac{n}{2}})=A_0(\omega_n^{2k+n})+A_1(\omega_n^{2k+n})\omega_n^{k+\frac{n}{2}}=A_0(\omega_\frac{n}{2}^{k})-A_1(\omega_\frac{n}{2}^{k})\omega_n^{k} \]

在求出 \(A_0(\omega _n^k),A_1(\omega _n^k)\) 后我们就能同时得到 \(A(\omega _n^k),A(\omega _n^{k+\frac{n}{2}})\) ，所以对 \(A_0,A_1\) 分别进行递归求解

特别的，基于分治 FFT 处理的多项式长度只能是 \(2^{b\in N^+}\) ，所以对于不是二整数次幂的形式，都需要补齐再计算

逆变换

通过多项式 \(A(x)\) 的点值求系数，设代入 \(\omega _n^0,\omega _n^1,\cdots,\omega _n^{n-1}\) 得到的点值为 \(y_0,y_1,\cdots,y_{n-1}\ (y_i=\sum\limits_{j=0}^{n-1} a_j(\omega_n^i)^j)\)

构造多项式 \(B(x)\)：

\[B(x)=y_0+y_1x+\cdots+y_{n-1}x^{n-1} \]

将单位根的倒数 \(\omega _n^0,\omega _n^{-1},\cdots,\omega _n^{-(n-1)}\)

\[\omega _n^k=\cos \theta +i\sin \theta\\ \frac{1}{\omega _n^k}=\frac{1}{\cos \theta +i\sin \theta}=\cos \theta -i\sin \theta=\cos (-\theta) +i\sin (-\theta) \]

代入 \(B(x)\) 得到新点值为 \(z_0,z_1,\cdots,z_{n-1}\)，其中：

\[z_k=\sum\limits_{i=0}^{n-1} y_i(\omega_n^{-k})^i=\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{n-1} a_j(\omega_n^i)^j(\omega_n^{-k})^i=\sum\limits_{j=0}^{n-1}a_j\sum\limits_{i=0}^{n-1}(\omega_n^{j-k})^i\\ \sum\limits_{i=0}^{n-1}(\omega_n^{j-k})^i= \left\{ \begin{array}{l} \sum\limits_{i=0}^{n-1}1=n & j=k\\ (\omega_n^{j-k})^n=(\omega_n^n)^{j-k}=0 & j\ne k \end{array} \right. \]

所以 \(z_k=na_k\) ，通过 \(\omega_n^{-k}\) 确定的点值逆变换后可以确定原函数的系数

基于递归实现的 FFT

void FFT(vector<complex<double>> &A,int n,int op){
	if (n==1) return;
	vector<complex<double>> A0(n/2),A1(n/2);
	for (int i=0;i<n/2;i++)
		A0[i]=A[i*2],A1[i]=A[i*2+1];
	FFT(A0,n/2,op),FFT(A1,n/2,op);
	complex<double> w1({cos(2*PI/n),sin(2*PI/n)*op});
	complex<double> wk({1,0});
	for (int i=0;i<n/2;i++){
		A[i]=A0[i]+A1[i]*wk;
		A[i+n/2]=A0[i]-A1[i]*wk;
		wk=wk*w1;
	}
}

op 参数表示当前执行的是正变换还是逆变换，区别在于对 \(\omega_n^k\) 的符号控制

基于迭代实现的 FFT

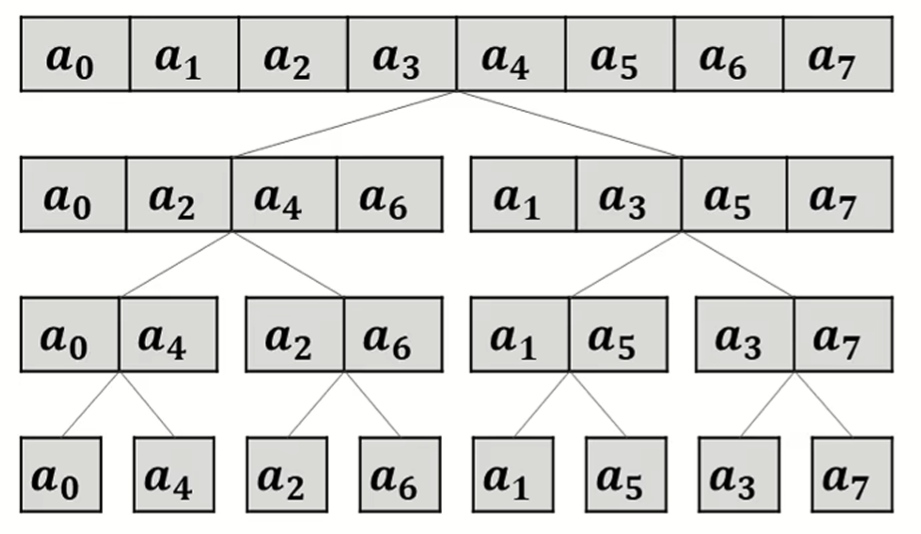
image-20250808142932444

原序列分治到底层后变换的序列存在一个规律：

  • 每个数用二进制表示，将二进制翻转对称一下，就是最终那个位置的下标，例如 \(a_1=001_2,a_4=100_2\) ，我们称这个变换为位逆序置换

根据定义的方法，我们可以在 \(O(n\log n)\) 的时间复杂度内求出每个数变换后的结果

事实上，还可以通过 \(O(n)\) 的递推时间复杂度实现，设 \(n=2^k\) ，\(k\) 表示二进制数的长度

设 \(R_x\) 为长度为 \(k\) 的二进制数 \(x\) 翻转后的结果，存在这样的递推关系：

\[R_x=\frac{R_{\frac{x}{2}}}{2} +(x\ \mathrm{mod}\ 2)\times \frac{n}{2} \]

从小到大求 \(R_x\) ，\(R_{\frac{x}{2}}\) 的值已知。把 \(x\) 除以二（右移一位）然后翻转再除以二，就得到了 \(x\) 除开二进制个位之外其他位翻转的结果，再单独考虑二进制个位的影响，如果翻转前个位是 \(1\) ，那么翻转后的最高位也为 \(1\)

void change(vector<complex<double>> &A,int n){
	vector<int> R(n,0);
	for (int i=0;i<n;i++)
		R[i]=(R[i>>1]>>1)+((i&1)?(n>>1):0);
	for (int i=0;i<n;i++)
		if (i<R[i]) swap(A[i],A[R[i]]);
}

利用位逆序变换得到后序列，然后自底向上合并

void FFT(vector<complex<double>> &A,int n,int op){
	change(A,n);
	for (int m=2;m<=n;m<<=1){//枚举分治块的长度
		complex<double> w1({cos(2*PI/m),sin(2*PI/m)*op});
		for (int i=0;i<n;i+=m){//枚举块的个数
			complex<double> wk({1,0});
			for (int j=0;j<m/2;j++){//
				complex<double> x=A[i+j],y=A[i+j+m/2]*wk;
				A[i+j]=x+y;
				A[i+j+m/2]=x-y;
				wk=wk*w1;
			}
		}
	}
}

优化高精度乘法

void solve(){
	string sa,sb;
	cin>>sa>>sb;
	int n=sa.size(),m=sb.size();
	for (int i=n-1;i>=0;i--) a[n-i-1]=sa[i]-'0';
	for (int i=m-1;i>=0;i--) b[m-i-1]=sb[i]-'0';
	int nm=n+m;
	for (n=1;n<=nm;n<<=1);
	FFT(a,n,1),FFT(b,n,1);
	for (int i=0;i<n;i++) ab[i]=a[i]*b[i];
	FFT(ab,n,-1);
	vector<int> ans;
	for (int i=0,t=0;i<n;i++){
		t+=(ab[i].real()/n+0.5);
		ans.push_back(t%10);
		t/=10;
	}
	while (ans.size()>1&&ans.back()==0) ans.pop_back();
	for (int i=ans.size()-1;i>=0;i--) cout<<ans[i];
}

将十进制数看作一个 \(x=10\) 的函数 \(A(x)\) ，每个系数 \(a_{i}\) 表示第 \(i+1\) 位上的数

同样的，将读入的两个数 \(a,b\) 转化为数组存储后利用 FFT 计算出点值，然后通过点值乘法计算 \(a\times b\) 映射的点值

再通过 FFT 逆变换计算出系数，最后按位取模得到拆分下来的十进制的每一位

posted @ 2025-08-08 20:34  才瓯  阅读(13)  评论(0)    收藏  举报