牛客 周赛100 20250720
牛客 周赛100 20250720
https://ac.nowcoder.com/acm/contest/112576
A:
题目大意:
void solve(){
int n;
cin>>n;
for (int i=1;i<=n;i++)
cout<<i<<' '<<i<<' ';
}
签到
B:
题目大意:

void solve(){
int n;
cin>>n;
vector<int> a(2*n);
for (int i=0;i<2*n;i++) cin>>a[i];
set<int> st;
vector<int> u,v;
for (auto x:a){
if (st.count(x)){
u.push_back(x);
continue;
}
st.insert(x);
v.push_back(x);
}
for (auto x:u) cout<<x<<' ';
cout<<endl;
for (auto x:v) cout<<x<<' ';
}
set 判重,答案存进 vector 内
C:
题目大意:

void solve(){
int n;
cin>>n;
vector<int> a(2*n);
for (auto &x:a) cin>>x;
stack<int> st;
set<int> m;
for (auto x:a){
if (m.count(x)){
while (st.top()!=x){
m.erase(st.top());
st.pop();
}
m.erase(st.top());
st.pop();
continue;
}
st.push(x);
m.insert(x);
}
if (st.size()) cout<<"No"<<endl;
else cout<<"Yes"<<endl;
}
用栈模拟,每次从最小的满足条件的区间开始删一定正确,时间复杂度为 \(O(n\log n)\)
也可以从左到右依次枚举端点,因为所有数都会被删除,那么数列的第一个数一定会被删,否则不能完全删去
每次都模拟删去当前数列第一个数的所满足区间,然后将这个区间的下一个数视为新的数列起点,时间复杂度 \(O(n)\)
void solve(){
int n;
cin>>n;
vector<int> a(2*n);
for (auto &x:a) cin>>x;
int p=0;
for (int i=1;i<2*n;i++){
if (a[i]==a[p]){
i++;
p=i;
}
}
if (p==2*n) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
D:
题目大意:

void solve(){
int n;
cin>>n;
vector<int> a(2*n+1);
for (int i=1;i<=2*n;i++) cin>>a[i];
vector<int> L(n+1,2*n);
LL ans=0;
int tl=2*n+1,tr=0;
for (int i=1;i<=2*n;i++){
L[a[i]]=min(L[a[i]],i);
if (L[a[i]]<i){//如果当前元素存在左端点,那么i就为右端点
ans+=i-L[a[i]]-1;//计算这个元素的f函数
tl=min(tl,i);//更新tl
}
tr=max(tr,L[a[i]]);//更新tr
}
cout<<ans+max(0,2*(tr-tl))<<endl;
}
每次交换操作可以视为交换两个区间的端点,当且仅当这两个区间互不相交时交换端点才能使得权值变大
L[x] 表示以元素 \(x\) 为端点的区间的左端点,tl,tr 表示最靠左的完整区间的右端点和最靠右的完整区间的左端点
交换端点后新增加的权值为 \(2\times (tr-tl)\)
E:
题目大意:
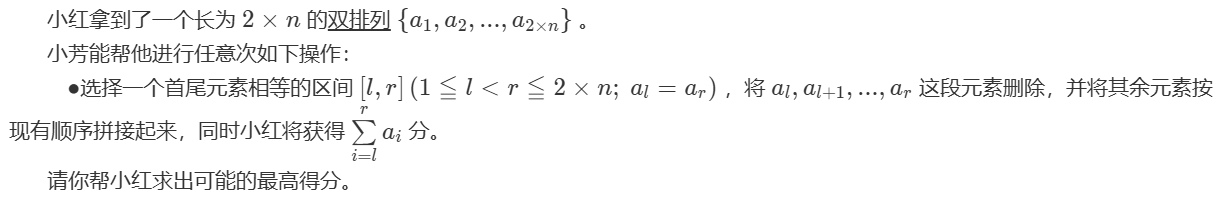
LL dp[400010][2];
void solve(){
int n;
cin>>n;
vector<int> a(2*n+1);
vector<LL> p(2*n+1);
for (int i=1;i<=2*n;i++) cin>>a[i];
for (int i=1;i<=2*n;i++) p[i]=p[i-1]+a[i];
vector<int> pos(2*n+1,0);
for (int i=1;i<=2*n;i++){
if (!pos[a[i]]){
dp[i][0]=max(dp[i-1][0],dp[i-1][1]);
pos[a[i]]=i;
}else{
dp[i][0]=max(dp[i-1][0],dp[i-1][1]);
dp[i][1]=max(dp[pos[a[i]]-1][0],dp[pos[a[i]]-1][1])+p[i]-p[pos[a[i]]-1];
}
}
cout<<max(dp[2*n][0],dp[2*n][1])<<endl;
}
因为删除区间后会导致左右部分的改变,且左右部分的分数是独立的,那么考虑动态规划
\(dp_{i,0/1}\) 表示数组从 \([1,i]\) 上(0/1,不删除/删除)以 \(a_i\) 为右端点的区间后的最高分数
使用 pos 数组记录元素 \(a_i\) 的左端点,状态转移方程可以被表示为:
如果当前的 \(a_i\) 还不能形成一个完整的区间
如果 \(a_i\) 已经能形成一个完整区间,考虑删去区间后的状态,用前缀和 p 维护区间和
如果删去以 \(a_i\) 为右端点的区间,那么状态从 \(a_i\) 所在区间的左端点的前一个元素转移,同时加上区间和
F:
题目大意:

const int mod=1e9+7;
LL ksm(LL a,LL b,LL p){
LL res=1;
while (b){
if (b&1) res=res*a%p;
a=a*a%p;
b>>=1;
}
return res;
}
void solve(){
int n;
cin>>n;
vector<int> b(2*n);
for (int i=0;i<2*n;i++) cin>>b[i];
sort(b.begin(),b.end());
LL ans=0,cnt=1;
for (int i=0;i<2*n;i++){
ans=(ans+100*cnt*ksm(b[i],mod-2,mod)%mod)%mod;
if (i%2) cnt++;
}
cout<<ans<<endl;
}
简单版本的题目不考虑失败的后果,所以使得一个数增加 \(1\) 的期望操作次数就是概率的倒数,且每一步之间都是独立的
那么用加法原理就能计算出总的期望步数,显然的有贪心的想法,将概率较大的操作放在较大的数上
所以对概率数组从小到大排序后,按照 \(1,1,2,2,\cdots,n,n\) 的顺序计算
G:
题目大意:

const int mod=1e9+7;
LL dp[101][100010];
LL ksm(LL a,LL b,LL p){
LL res=1;
while (b){
if (b&1) res=res*a%p;
a=a*a%p;
b>>=1;
}
return res;
}
void solve(){
int n;
cin>>n;
vector<int> b(2*n);
for (int i=0;i<2*n;i++) cin>>b[i];
sort(b.begin(),b.end());
LL ans=0;
LL inv100=ksm(100,mod-2,mod);
for (int p=1;p<=100;p++){
LL P=p*inv100%mod;
LL invp=ksm(P,mod-2,mod);
for (int i=1;i<=100000;i++)
dp[p][i]=(1+dp[p][i-1]*(1-P+mod)%mod)*invp%mod;
for (int i=1;i<=100000;i++)
dp[p][i]=(dp[p][i-1]+dp[p][i])%mod;
}
int cnt=1;
for (int i=0;i<2*n;i++){
ans=(ans+dp[b[i]][cnt])%mod;
if (i%2) cnt++;
}
cout<<ans<<endl;
}
比较经典的概率DP,因为是计算期望步数而不是计算总概率,那么设置 \(dp_{i,j}\) 表示在概率为 \(i\%\) 的情况下,从 \(j-1\) 到 \(j\) 的期望步数
考虑状态的转移:
含义是从 \(j-1\) 到 \(j\) 的期望步数由两部分组成,第一部分是有 \(i\%\) 的概率之间从 \(j-1\) 加上 \(1\) 得来
第二部分是考虑有 \((1-i\%)\) 的概率后退一步到 \(j-2\) , 那么考虑从 \(j-2\) 到 \(j-1\) 的期望步数 \(dp_{i,j-1}\) ,再加上从 \(j-1\) 到 \(j\) 的期望步数 \(dp_{i,j}\) ,以及后退的步数 \(1\) ,最后得到方程。两侧移动后得到只由 \(dp_{i,j-1}\) 转移的方程
在题目时空允许的情况下可以预处理出所有的 \(dp_{i,j}\) ,累加每一步的期望步数得到总的期望步数
最后根据贪心依次计算答案



 浙公网安备 33010602011771号
浙公网安备 33010602011771号