牛客 周赛99 20250712

牛客 周赛99 20250712

https://ac.nowcoder.com/acm/contest/112544

A：

void solve(){
	string s;
	cin>>s;
	for (int i=0;i<s.size()-1;i++){
		if (s[i]=='9'&&s[i+1]=='9'){
			cout<<"YES"<<endl;
			return;
		}
	}
	cout<<"NO"<<endl;
}

签到

B：

题目大意：给出一格字符串，判断至少需要多长的 ASCII 码表才能完整输出这些字符

void solve(){
	int n;
	cin>>n;
    int ans=0;
	for (int i=1;i<=n;i++){
        char c;
        cin>>c;
        ans=max(ans,(int)c);
    }
    cout<<ans<<endl;
}

记录 ASCII 码最大的字符即可

C：
题目大意：

void solve(){
	int k;
	cin>>k;
	if (k==0){
		cout<<1<<endl;
		return;
	}
	if (k&1){
		cout<<4;
		for (int i=1;i<=k/2;i++) cout<<8;
	}else{
		for (int i=1;i<=k/2;i++) cout<<8;
	}
	cout<<endl;
}

贪心，如果能在当前位放 \(8\) ，则放 \(8\) 是最优的

因为前导 \(0\) 不参与计算，所以当洞数为奇数时，首位放 \(4\) 一定优，其余位则放 \(8\) ，用更少的数累加得到更多的洞数

特别的，当 \(k=0\) 时，特判为 \(1\)

D：

题目大意：

void solve(){
	LL x,p;
	cin>>x>>p;
	
	if (x==1){
		cout<<2*p-1<<endl;
		return;
	}
	if (p<x){
		cout<<2*p<<endl;
		return;	
	}else{
		if (p%x==0)
			cout<<p/x*2-1<<endl;
		else
			cout<<2*((x-1)*(p/x)+p%x)<<endl;
	}
}

可以观察到这样一个性质：

当 \(k\%x=0\) 时，这一位的元素才为奇数，否则都为偶数，这是因为当且仅当 \(k\%x=0\) 时 \(\lfloor\frac{k}{x}\rfloor\) 的奇偶性才发生改变，且这时的前缀和的奇偶性也发生改变，那么只有这一位为奇数，\(\lfloor\frac{k}{x}\rfloor\) 分块内的元素为偶数才满足

所以可以根据周期性来计算 \(p\) 位上的数

• 当 \(p<x\) 时，第一段分块内的数都是偶数

• 当 \(p\ge x\) 时，判断是否在分界点上（奇数），否则计算偶数的个数

  \[a_p=2\times (x-1) \times(\lfloor\frac{p}{x}\rfloor)+p\%x \]

• 特别的，当 \(x=1\) 时，数组全为奇数

E：
题目大意：

int a[200010];

void solve(){
	int n;
	cin>>n;
	for (int i=1;i<=n;i++) cin>>a[i];
	map<int,int> mp;
	for (int i=1;i<=n;i++) mp[a[i]]++;
	int r=n;
	a[n+1]=1e9+1;
	while (r>=1&&a[r]>=r&&a[r]<a[r+1]&&mp[a[r]]==1) r--;
	set<int> st;
	for (int i=1;i<=r;i++)
		if (a[i]!=i) st.insert(a[i]);
	cout<<st.size()<<endl;
}

如果存在一段连续严格单调递增的前缀串，当到某一位出现 \(a_i\le a_{i-1}\) 时，区间 \([1,i]\) 上，所有的数都需要被修改，且修改后 \(a_i=i\)

所以可以找到一个分界点，分界点左边的元素需要修改为 \(a_i=i\) 右边的数则不需要修改

所以从后往前遍历找分界点 \(r\) ，当满足 \(a_r\ge r\) 且 \(a_r<a_{r+1}\) 时才能向左扩展

需要注意的是，如果 \(a_r\) 在 \(r\) 之前已经出现过一次了，那么就需要停止

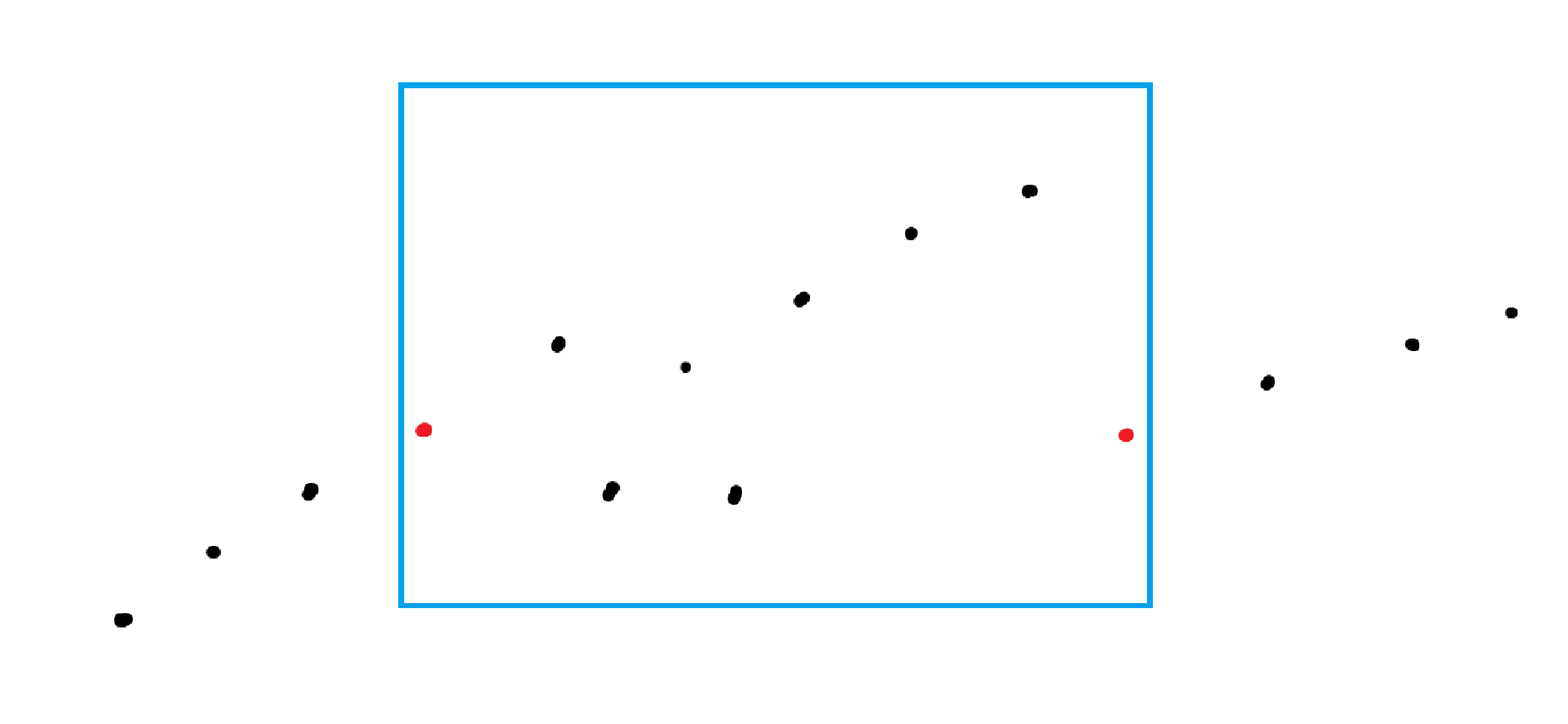
将元素大小转化成折线图，当一段区间的左右端点值相同时，无论中间的情况如何，这一段区间一定需要修改

while (r>=1 && a[r]>=r && a[r]<a[r+1] && mp[a[r]]==1) r--;

找到分界点后，遍历这一段前缀区间，需要修改的次数为 \(a_i\ne i\) 的个数

F：

题目大意：\(n\) 个糖果分给 \(m\) 个人，计算最后所有人分到的糖果数最大按位与的数值

void solve(){
	LL n,m;
	cin>>n>>m;
	LL ans=0;
	
	if (m==1){
		cout<<n<<endl;
		return;
	}
	
	for (int i=30;i>=0;i--){
		if (n>=m*(1<<i)){
			ans+=(1<<i);
			n-=m*(1<<i);
		}else if (n>=m*((1<<i)-1)){
			LL k=(n-m*((1<<i)-1)+(1<<i)-1)/(1<<i);
			n-=k*(1<<i);
		}
	}
	cout<<ans<<endl;
}

从最高位到最低位贪心，存在三种情况：

• 当前的 \(n\) 比这一位 \(i\) 全放 \(1\) 的数值还大，那么这一位就可以填 \(1\)

• 当前的 \(n\) 比这一位 \(i\) 全放 \(1\) 小，但是比 \(i-1\) 之后的所有位都放 \(1\) 还大，如果后面全放 \(1\) ，那么最后必然会剩下某些糖果，所以在 \(i\) 位上需要放某些 \(1\) 使得部分糖果浪费掉（必要的牺牲）

  \[k=\lceil \frac{n-m*(2^i-1)}{2^i} \rceil \]

  需要在这一位填 \(1\) 的个数是上取整的

• 当前的 \(n\) 比 \(i-1\) 位之后所有位都放 \(1\) 还小，那么就重新考虑 \(i-1\) 的情况