牛客 周赛93 20250524
牛客 周赛93 20250524
https://ac.nowcoder.com/acm/contest/109904
A:
题目大意:
void solve(){
int n;
cin>>n;
if (pow(2,n)>pow(n,3)) cout<<"B";
else cout<<"A";
}
签到
B:
题目大意:给定字符串 \(s\) ,计算长度为 \(5\) 的连续完美对称子串数量,(连续完美对称子串:当且仅当第 \(1,3,5\) 个字符相同,第 \(2,4\) 个字符相同,且第 \(1,2\) 个字符不同)
void solve(){
string s;
cin>>s;
int ans=0;
for (int i=0;i+4<s.size();i++){
if (s[i]==s[i+2]&&s[i]==s[i+4]&&s[i+1]==s[i+3]&&s[i]!=s[i+1])
ans++;
}
cout<<ans;
}
暴力枚举,没什么好说的
C:
题目大意:

void solve(){
int n,sx,sy,ex,ey;
cin>>n;
cin>>sx>>sy>>ex>>ey;
int da=abs(2-sx)+abs(n-sy);
int db=abs(2-ex)+abs(n-ey);
if(da==db){
cout<<"YES";
}else{
if (abs(sx-ex)==1&&abs(sy-ey)==1&&max(sy,ey)+1<n)
cout<<"YES";
else
cout<<"NO";
}
}
一开始横纵坐标写反了卡了十多发
显然有:如果两个坐标离 \((2,n)\) 的曼哈顿距离相同,那么不放障碍就能满足题意
如果要放障碍,那么放一个障碍就足够,多放障碍没有作用,且障碍必须放置在第二行上
因为放在第一行的障碍不会缩短初始坐标在第一行的人到终点的最短距离,这个人在路径中必然存在一次向下移动
所以如果要放障碍,那么存在一个人的初始坐标在第二行,这个人因为障碍而额外增加的步数为 \(2\) ,即向上向下各一次
那么这两个人初始坐标需要满足横纵坐标差的绝对值都为 \(1\) ,如图:
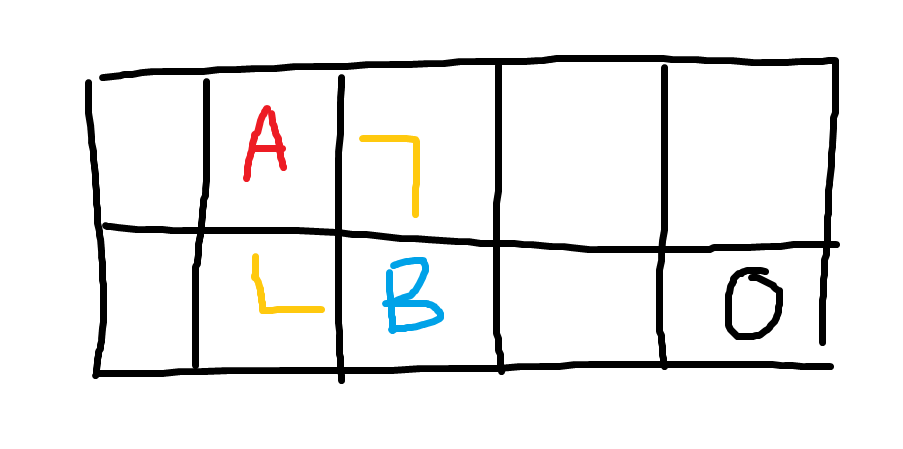
还要判断能否放得下障碍,即第二行的人到终点的距离需要大于 \(1\)
D:
题目大意:

void solve(){
int n,k;
cin>>n>>k;
vector<LL> a(n+1);
for (int i=1;i<=n;i++) cin>>a[i];
vector<pair<LL,int>> b;
for (int i=2;i<=n;i++) b.push_back({a[i],i});
auto cmp=[](pair<LL,int> x,pair<LL,int> y){
if(x.first!=y.first) return x.first>y.first;
else return x.second>y.second;
};
sort(b.begin(),b.end(),cmp);
vector<bool> st(n+1,0);
for (int i=0;i<k;i++){
a[1]+=b[i].first;
st[b[i].second]=1;
}
for (int i=1;i<=n;i++)
if (!st[i]) cout<<a[i]<<' ';
cout<<endl;
}
贪心算法,把较大的数加到 \(a_1\) 上一定最优
所以记录 \(a_2,a_3,\cdots,a_n\) 的数值和所在的位置,排序后取前 \(k\) 个最大数,并记录需要删除的位置
但是排序过程中存在一个问题,假如 \(a_3=a_5\) 数值相同时应该先取谁?取后面的更优
简单证明:在取 \(a_3,a_5\) 时,后面的元素中一定不存在大于 \(a_3\) 的元素,所以对于 \(a_3,a_4,a_5,a_6\) 而言,一定有 \(a_4,a_6\le a_3,a_5\)
取走 \(a_3\),剩余元素的字典序列为 \(a_4,a_5,a_6\) , 取走 \(a_5\),剩余元素的字典序列为 \(a_3,a_4,a_6\)
明显的, \(a_4,a_5,a_6\) 的字典序小于等于 \(a_3,a_4,a_6\) 的字典序,所以取较后面的最优
E:
题目大意:

const int mod=1e9+7;
int a[1000010];
int mp[1000010];
LL p[1000010];
void solve(){
int n;
cin>>n;
for (int i=1;i<=n;i++) cin>>a[i];
for (int i=1;i<=n;i++) mp[a[i]]++;//记录元素数量
p[0]=1;
for (int i=1;i<=n;i++)
p[i]=p[i-1]*2%mod;
LL ans=0;
for (int i=1;i<=n;i++)
ans=(ans+p[mp[i]]-1)%mod;
LL sum=1;
for (int i=0;i<=n;i++){
if (mp[i]==0) break;
sum=sum*(p[mp[i]]-1)%mod;
ans=(ans+sum)%mod;
}
cout<<ans;
}
\(mex=0\) 时满足题意的情况下有 \(max=min\) ,则对每一个值不为 \(0\) 的元素,自身形成的子串都满足题意
for (int i=1;i<=n;i++)
ans=(ans+p[mp[i]]-1)%mod;
值为 \(i\) 的元素能形成的非空子串个数为 \(2^{mp_i}-1\) ,即每个元素的选择数 \(2^{mp_i}\) 减去空串的 \(1\)
\(mex\ne 0\) 时,根据定义,选出的子串一定有值为 \([0,mex-1]\) 的元素,且个数至少为 \(1\) ,那么 \(min\) 一定为 \(0\)
满足题意时,\(max\le mex-0\) 又因为 \(max\ne mex\) ,所以 \(max=mex-1\)
那么从 \(i=0\) 开始遍历,如果遇到 \(mp_i=0\) ,则说明序列元素值不连续,直接中断
LL sum=1;
for (int i=0;i<=n;i++){
if (mp[i]==0) break;
sum=sum*(p[mp[i]]-1)%mod;
ans=(ans+sum)%mod;
}
令 \(sum_i\) 表示 \(max=i\) 时的子串数量,且根据乘法原理 \(max=i+1\) 的子串数量为 \(sum_i\times (2^{mp_{i+1}}-1)\)
对答案的贡献为 \(\sum_{i=1}^k sum_i\)
F:
题目大意:

const int mod=1e9+7;
int g[510][510];
LL dp[510][510][510];
void solve(){
int n;
cin>>n;
for (int i=1;i<=n;i++)
for (int j=1;j<=i;j++)
cin>>g[i][j];
if (n%2)
for (int i=1;i<=n/2+1;i++)
dp[n/2+1][i][i]=1;
else
for (int i=1;i<=n/2;i++)
for (int j=i;j<=i+1;j++)
if (g[n/2][i]==g[n/2+1][j])
dp[n/2][i][j]+=1;
for (int k=n/2;k>=1;k--){
for (int i=1;i<=k;i++){
for (int j=1;j<=(n+1-k);j++){
if (g[k][i]==g[n+1-k][j]){
dp[k][i][j]+=dp[k+1][i][j]+
dp[k+1][i+1][j]+
dp[k+1][i][j-1]+
dp[k+1][i+1][j-1];
dp[k][i][j]%=mod;
}
}
}
}
LL ans=0;
for (int i=1;i<=n;i++) ans=(ans+dp[1][1][i])%mod;
cout<<ans;
}
根据回文串的特性,\(s_i=s_{n-i+1}\) 得到最小回文子串为 \(s_{n/2},s_{n/2+1}\) (n为偶数),\(s_{n/2+1}\) (n为奇数)
所以状态转移应该从字符串的中间开始向两侧转移,设 \(dp_{i,j,u,v}\) 表示第 \(i\) 行第 \(j\) 列与第 \(u\) 行第 \(v\) 列的元素构成回文串的路径数
那么状态转移方程为:\(g_{i,j}\) 表示三角形上坐标为 \((i,j)\) 的元素
因为奇偶性的不同,所以状态的初始化也不同
\(n\) 为奇数:最小回文子串为 \(s_{n/2+1}\) ,所以对所有的 \(dp_{n/2+1,i,n/2+1,i}\) 初始化为 \(1\) ,表示选第 \(n/2+1\) 行的任意单个元素都能构成回文串
\(n\) 为偶数:最小回文子串为 \(s_{n/2},s_{n/2+1}\) ,则需要先处理这两行的回文子串,当 \(g_{i,j}=g_{i+1,j},g_{i,j}=g_{i+1,j+1}\) 时,那么 \(dp_{i,j,i+1,j},dp_{i,j,i+1,j+1}\) 为 \(1\)
特别的,因为每一层的状态 \(dp_{i,j,u,v}\) 都由 \(dp_{i+1,j,u-1,v}\) 转移,且 \(u=n+1-i\) ,所以可以优化掉 \(u\) 层空间



 浙公网安备 33010602011771号
浙公网安备 33010602011771号