牛客 周赛92 20250515

牛客 周赛92 20250515

https://ac.nowcoder.com/acm/contest/108589

A：

题目大意：

void solve(){
	int n;
	cin>>n;
	cout<<"a_";
	for (int i=3;i<=n;i++) cout<<'a';
}

签到，随便构造就行

B：
题目大意：

char g[1010][1010];
int n,m;
int dx[]={0,1};
int dy[]={1,0};
vector<char> path;

bool dfs(int x,int y){
	if (x==n&&y==m){
		for (auto it:path) cout<<it;
		return 1;
	}
	for (int i=0;i<2;i++){
		int tx=x+dx[i],ty=y+dy[i];
		if (tx<1||ty<1||tx>n||ty>m)	continue;
		if (g[tx][ty]=='#') continue;
		if (i==0) path.push_back('D');
		else path.push_back('S');
		if (dfs(tx,ty)) return 1;
		path.pop_back();
	}
	return 0;
}

void solve(){
	cin>>n>>m;
	for (int i=1;i<=n;i++)
		for (int j=1;j<=m;j++)
			cin>>g[i][j];
	bool f=dfs(1,1);
}

DFS爆破，用path存路径

C：
题目大意：

void solve(){
	int n;
	cin>>n;
	if (n<=2){
		cout<<-1;
		return;
	}
	cout<<1<<' ';
	for (int i=n;i>1;i--) cout<<i<<" ";
}

显然当 \(n\le 2\) 时无解，考虑普通情况

存在这样一个特殊的序列 \(a=\{1,n,n-1,n-2,\cdots ,2\}\)，那么退化一次后的序列为 \(b=\{n-1,1,1,\cdots,1\}\)

退化两次后的序列为 \(c=\{n-2,0,0,\cdots,0\}\) 满足题意，此后的所有退化序列都为 \(\{n-2,0,\cdots,0\}\)

D：
题目大意：给出正整数 \(k\) ，需要找到两个正整数满足 \(p+q=k\) ，并且 \(x^2-px+q=0\) 存在两个正整数解

void solve(){
	LL k;
	cin>>k;
	if (k<=2){
		cout<<-1;
		return;
	}
	for (LL a=1;a<=sqrt(k);a++){
		LL b=(k-a)/(a+1);
		if (b==0) break;
		if ((k-a)%(a+1)==0){
			cout<<a+b<<' '<<a*b;
			return;
		}
	}
    cout<<-1;
}

方程 \(x^2-px+q=0\) 可以被分解为 \((x-a)*(x-b)=0\) ，其中

\[a*b=q,a+b=p\\ a,b\in N^+ \]

所以 \(p+q=k=(a+b)+a*b\)，则 \(b\) 被表示为 \((k-a)/(a+1)\) ，枚举 \(a\) 然后判断 \(b\) 是否满足条件

又因为 \(k+1=(a+1)*(b+1)\) ，只需要找到其中一个因数即可，那么最多枚举到 \(sqrt(k)+1\) 即可

时间复杂度为 \(O(\sqrt n)\)

E：
题目大意：

struct node{
	int l,r;
};
node tr[100010];
int lm[10010];
int idx;

void dfs(int dep,int p){
	tr[p].l=tr[p].r=-1;
	if (lm[dep+1]){
		tr[p].l=++idx;
		dfs(dep+1,tr[p].l);
		lm[dep+1]--;
	}
	if (lm[dep+1]){
		tr[p].r=++idx;
		dfs(dep+1,tr[p].r);
		lm[dep+1]--;
	}
}

void solve(){
	int n;
	cin>>n;
	int sum=0;
	for (int i=1;i<=n;i++){
		cin>>lm[i];
		sum+=lm[i];
	} 
	dfs(0,1);
	cout<<1<<endl;
	for (int i=1;i<=sum;i++) 
		cout<<tr[i].l<<' '<<tr[i].r<<endl;
}

DFS 建树，如果当前节点的下一层有空间，那么就给这个节点添加儿子并编号

F：
题目大意：

int g[510][510];

void solve(){
	int n,m;
	cin>>n>>m;
	int d=0;
	for (int i=1;i<=n+m;i++) d^=i;
	if (d) {cout<<-1<<endl; return;}
	if (n>=m){
		for (int i=1;i<n;i++) g[i][min(i,m)]=i;
		for (int i=1;i<m;i++) g[n][i]=i^(n+i);
		g[n][m]=n+m;
		for (int i=m;i<n;i++) g[n][m]^=g[i][m];
	}else{
		for (int i=1;i<m;i++) g[min(i,n)][i]=i;
		for (int i=1;i<n;i++) g[i][m]=i^(m+i);
		g[n][m]=n+m;
		for (int i=n;i<m;i++) g[n][m]^=g[n][i];
	}
	for (int i=1;i<=n;i++){
		for (int j=1;j<=m;j++){
			cout<<g[i][j]<<' ';
		}
		cout<<endl;
	}
}

对于行列异或和为排列的情况下存在这样一个必要条件：

\[\bigoplus_{i=1}^{n} \bigoplus_{j=1}^m g_{i,j}\ \oplus\ \bigoplus_{j=1}^{m} \bigoplus_{i=1}^n g_{i,j}=\bigoplus_{k=1}^{n+m} \]

又因为对于一格上的元素在行列被选取了两次，所以上式为 \(0\)

需要知道 \(0\oplus x=x\) ，可以构造这样一个特殊的形式，空白处为 \(0\)

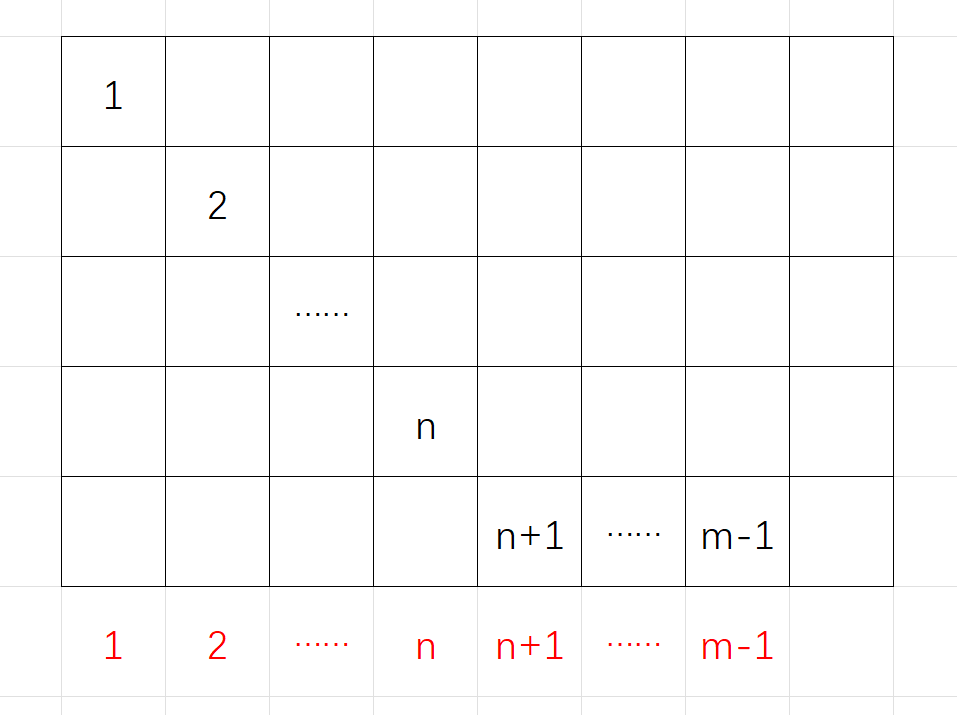
这样所有对所有列，异或和都是这一列所填数字本身，现在需要使得每一行的异或和为 \([m+1,n+m]\) ，那么可以构造

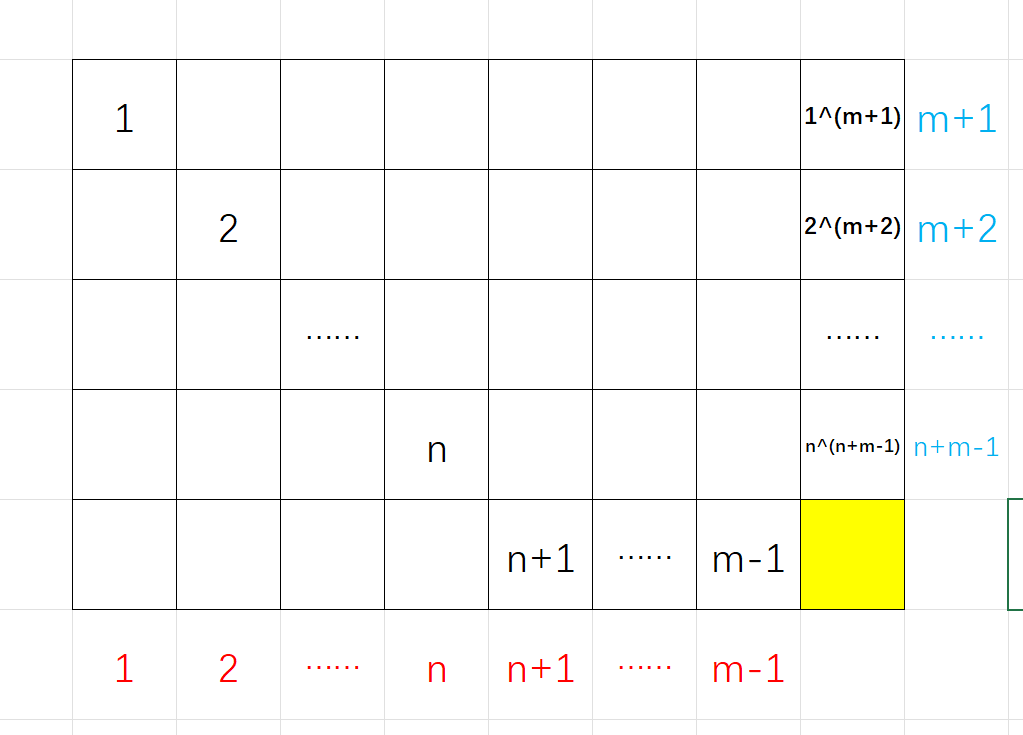
只剩下坐标为 \((n,m)\) 的格子需要填，且这个格子填上后需要满足 \(\bigoplus_{j=1}^{n} g_{i,j}=m,\bigoplus_{i=n}^{m}g_{i,j}=n+m\)

那么这种构造方案下需要满足

\[\left[\bigoplus_{i=1}^{i=n-1} i\oplus (i+m) \right]\oplus g_{n,m}=m\\ \left[\bigoplus_{j=n+1}^{j=m-1} j\right] \oplus g_{n,m} =n+m\\ \]

化简后得到

\[\bigoplus _{k=1}^{n+m} k=0 \]

与前面得出的必要条件相同，说明这种构造方式成立，且该条件为充分必要条件