牛客周赛91 20250501

https://ac.nowcoder.com/acm/contest/108038#question

A：

题目大意：

const string c="while";

void solve(){
	string s;
	cin>>s;
	int cnt=0;
	for (int i=0;i<5;i++){
		if (s[i]!=c[i]) cnt++;
	}
	cout<<cnt;
}

签到

B：

题目大意：给定一个数组，求连续 $10$ 个元素的最大元素和

LL a[100010];
LL p[100010];

void solve(){
	int n;
	cin>>n;
	for (int i=1;i<=n;i++){
		cin>>a[i];
		p[i]=p[i-1]+a[i];
	}
	LL mx=0;
	for (int i=1;i<=n;i++)
		mx=max(mx,p[i]-p[max(i-10,0)]);
	cout<<mx;
}

前缀和，注意处理边界

C：

题目大意：给定长度为 $n$ 的数组 $a$ ，找出元素和最大的逆序对

void solve(){
	int n;
	cin>>n;
	vector<int> a(n+1);
	for (int i=1;i<=n;i++) cin>>a[i];
	int ans=0,mx=0;
	for (int i=1;i<=n;i++){
		if(mx<a[i]) mx=a[i];
		else ans=max(ans,mx+a[i]);
	}
	cout<<ans<<endl;
}

贪心，两个元素满足逆序对的条件是存在 $a_i>a_j,i<j$

考虑用 $mx$ 记录当前枚举到的数之前的最大值，即贪心地固定 $a_i$ ，然后找一个最优的 $a_j$ 更新答案

对应每一个枚举到的 $a_i$ ，有两种情况：

$a_i<mx $ ，满足逆序对的条件，判断是否能更新答案
$a_i>mx$ 存在更优的 $mx$ 可以更新，那么一定要将 $mx$ 更新为 $a_i$ ，$i$ 之后合法的逆序对之和一定更优

D：

题目大意：给定长度为 $n$ 的数组 $a$，如果两个数 $a_i,a_j$ 的相对差为 $1$ ，则 $i,j$ 之间存在一条无向边，为了使 $[1,n]$ 所有节点都相互连通，求需要额外添加的边数

void solve(){
	int n;
	cin>>n;
	vector<int> a(n+1);
	map<int,int> mp;
	for (int i=1;i<=n;i++){
		cin>>a[i];
		mp[a[i]]++;
	}
	int cnt=0;
	int ans=0;
	for (auto [k,v]:mp){
		if (mp[k-1]==0) cnt++;
		if (mp[k-1]==0&&mp[k+1]==0) ans+=v-1;
	}
	cout<<cnt-1+ans<<endl;
	
}

对于每个节点对应的 $a_i$ ，可以先进行排序，这样下来所有的 $a_i$ 都依靠数值紧密的排列在一起

注意这里额外添加的边是作用于节点于节点之间的，而不是作用于值于值之间的

遍历排序后的序列，对于任意一个 $a_i$ （对应节点为 $x$ ），节点之间的连接关系存在两种情况

存在值为 $a_i-1$ 的节点 $y$ ，说明这个 $y$ 与 $x$ 间连接有一条边
不存在值为 $a_i-1$ 的节点 $y$ ，设序列中存在值为 $a_i-k,(k>1)$ 的节点 $y$ ，为了使节点之间相互连通，那么 $x,y$ 之间需要额外添加一条边
如果既不存在值为 $a_i-1,a_i+1$ 的节点，那么所有值为 $a_i$ 的节点之间都需要连边，即不能通过值为 $a_i-1,a_i+1$ 的节点进行中转

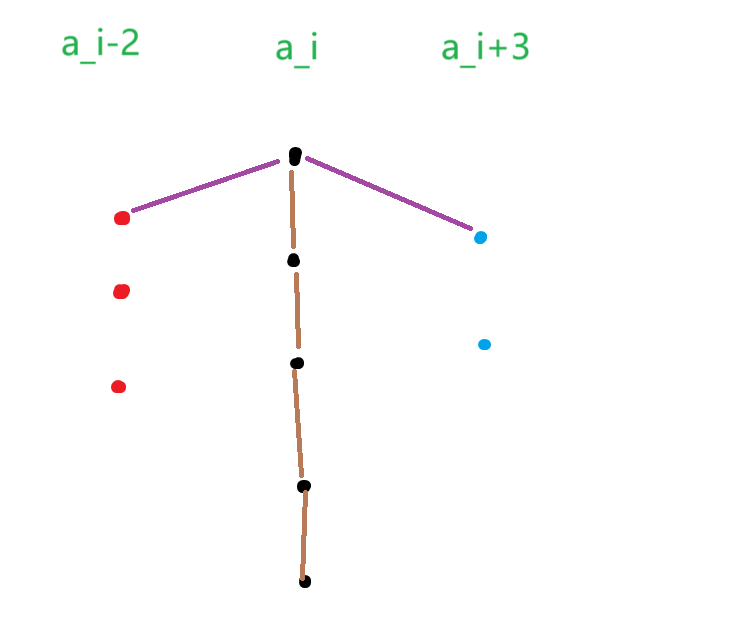
除开需要连接两条 $<a_i-2,a_i>,<a_i,a_i+3>$ 的路径外，在所有值为 $a_i$ 的点的内部都要连接边，这样添加的边数最少

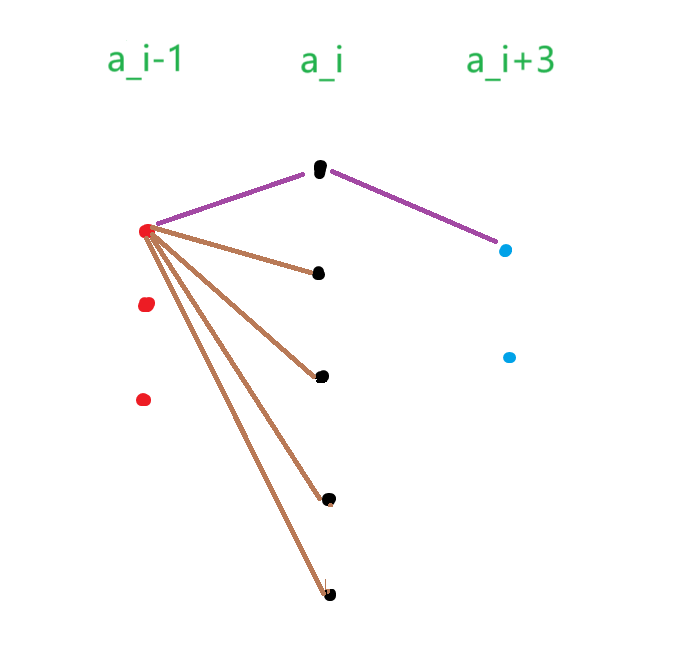
如果存在值为 $a_i-1$ 的节点，那么只需要额外连接一条边 $<a_i,a_i+3>$ ，则可以通过路径 $<a_i-1,a_i>$ 使得任意值为 $a_i+3$ 的节点与任意值为 $a_i$ 的节点相互连通

E：

题目大意：

char g[1010][1010];
int dx[]={1,0,-1,0};
int dy[]={0,1,0,-1};

void solve(){
	int n,m;
	cin>>n>>m;
	vector<int> c1(m+1),r1(n+1);
	int cc=0;
	for (int i=1;i<=n;i++)
		for (int j=1;j<=m;j++)
			cin>>g[i][j];
	for (int i=1;i<=n;i++){
		for (int j=1;j<=m;j++){
			if (g[i][j]=='1'){
				c1[j]++;
				r1[i]++;
				cc++;
			} 
		}
	}
	
	int col=0;
	for (int i=1;i<=m;i++)
		col+=(c1[i]==n);
	int row=0;
	for (int i=1;i<=n;i++)
		row+=(r1[i]==m);
	if ((col==2&&cc==2*n)||(row==2&&cc==2*m)||cc==0){
		cout<<"YES"<<endl;
		return;
	}
	
	for (int i=1;i<=n;i++){
		for (int j=1;j<=m;j++){
			if (g[i][j]=='0'){
				if (c1[j]==n-1&&r1[i]==m-1&&cc==c1[j]+r1[i]){
					cout<<"YES"<<endl;
					return;
				}
			}
		}
	}
	cout<<"NO"<<endl;
}

模拟题，在操作两次行或列的情况下，只会出现以下的布局情况

对于每种情况进行判断即可

for (int i=1;i<=n;i++){
	for (int j=1;j<=m;j++){
		if (g[i][j]=='1'){
			c1[j]++;//记录第j列上1的个数
			r1[i]++;//记录第i行上1的个数
			cc++;//记录1的总数
		} 
	}
}

按照图的方式进行判断比较繁琐，通过 $1$ 的个数进行判断更简洁

int col=0;
for (int i=1;i<=m;i++)
	col+=(c1[i]==n);
int row=0;
for (int i=1;i<=n;i++)
	row+=(r1[i]==m);
if ((col==2&&cc==2*n)||(row==2&&cc==2*m)||cc==0){
	cout<<"YES"<<endl;
	return;
}

如果恰好存在两行或两列上的 $1$ 的个数为这一行的数量或这一列的数量，并且 $1$ 的总数也恰好是这两行或两列 $1$ 的数量的总和

那么一定为上面更改两行或更改两列的情况，特别的如果 $1$ 的个数为 $0$ 也满足

最后一种情况的判断，可以找特殊点即行列交叉点

for (int i=1;i<=n;i++){
	for (int j=1;j<=m;j++){
		if (g[i][j]=='0'){
			if (c1[j]==n-1&&r1[i]==m-1&&cc==c1[j]+r1[i]){
				cout<<"YES"<<endl;
				return;
			}
		}
	}
}

如果存在一个 $0$ 点，他相邻的四方向都是 $1$ ，并且对应行列上的 $1$ 的数量恰好为 $1$ 的总数，那么该情况也合法

这是更改一行一列情况的充分必要条件，证明过程略

F：

题目大意：

const LL mod=998244353;
const LL N=1e6+10;

vector<LL> minp(N+1),pri;
LL inv[N+1];
LL tol[N+1],odd[N+1],d[N+1];

LL ksm(LL a,LL b,LL p){
	LL res=1;
	while(b){
		if (b&1) res=res*a%p;
		a=a*a%p;
		b>>=1;
	}
	return res;
}

void init(){
	for (LL i=2;i<=N;i++){
		if (!minp[i]){
			minp[i]=i;
			pri.push_back(i);
		}
		for (auto &p:pri){
			if (i*p>N) break;
			minp[i*p]=p;
			if (p==minp[i]) break;
		}
	}
	
	for (LL i=1;i<=N;i++) inv[i]=ksm(i,mod-2,mod);
	
	tol[0]=1,odd[0]=1;
	for (LL i=1;i<=N;i++){
		LL j=i;
		vector<pair<LL,LL>> pk;//分解j到每个质因子以及他的幂
		while (j>1){
			LL p=minp[j];
			LL k=0;
			while(j%p==0){//计算当前质因子p的幂
				j/=p;
				k++;
			}
			pk.push_back({p,k});
		}
		tol[i]=tol[i-1];
		odd[i]=odd[i-1];
		for (auto &[x,y]:pk){
			tol[i]=(tol[i]*inv[d[x]+1])%mod;
			if (x>2) odd[i]=(odd[i]*inv[d[x]+1])%mod;
			d[x]+=y;
			tol[i]=(tol[i]*(d[x]+1))%mod;
			if (x>2) odd[i]=(odd[i]*(d[x]+1))%mod;
		}
	}
}


void solve(){
	int n;
	cin>>n;
	cout<<(odd[n]*ksm(tol[n],mod-2,mod))%mod<<' ';
}

唯一分解定理，所有的数都能被他的质因子唯一表示

对于一个数 $d$，可以被表示为 $d=p_1^{\alpha_1}\times p_2^{\alpha_2} \times p_2^{\alpha_2}\times \cdots \times p_s^{\alpha_s}$ ，其中 $p_i$ 为 $d$ 的某个质因子

那么这个数的因子个数为 $\prod_{i=1}^s (\alpha_i+1)$ ，即对于每个质因子而言，都考虑他的幂数 $\alpha _i$ 对总因子个数的贡献

其中在 $p_i\ne 2$ 下计算出的因子个数为 $d$ 的奇数质因子个数，引理：所有的质数除开 $2$ 都是奇数

那么对于这个数 $d$ 答案可以被表示为：（${\rm{inv_{mod}}}(x)$ 表示 $x$ 在 $mod$ 下的逆元）

\[ans=\prod_{i=1,p_i\ne 2}^s (\alpha_i+1)\cdot {\rm{inv_{mod}}}(\prod_{i=1}^s (\alpha_i+1)) \]

因为询问次数较大，所有可以对所有在范围内的询问都做一次预处理，总时间复杂度为 $O(n\log n)$

for (LL i=2;i<=N;i++){
	if (!minp[i]){//计算i的最小质因子
		minp[i]=i;
		pri.push_back(i);
	}
	for (auto &p:pri){//欧拉筛
		if (i*p>N) break;
		minp[i*p]=p;
		if (p==minp[i]) break;
	}
}

posted @ 2025-05-04 15:40 才瓯阅读(34) 评论(0) 收藏举报

刷新页面返回顶部

从0.5开始的C语言学习

by 才瓯&dianmancolonel

牛客周赛91 20250501

从0.5开始的C语言学习

by 才瓯&dianmancolonel

牛客 周赛91 20250501

牛客周赛91 20250501