牛客 周赛90 20250424
牛客 周赛90 20250424
https://ac.nowcoder.com/acm/contest/107500
A:
题目大意:给定整数 \(n\) 判断是否为 \(2.5\) 的整倍数
void solve(){
LL n;
cin>>n;
if(n*10%25==0) cout<<"Yes";
else cout<<"No";
}
都扩大十倍,避免小数运算
B:
题目大意:给定包含 \(2,5\) 的字符串 \(s\) ,可以进行这样的操作:选择两个不同的下标 \(i,j\) ,交换 \(s_i,s_j\) ,求能使得字符串不存在 \(25\) 子序列的最小操作次数
void solve(){
int n;
cin>>n;
string s;
cin>>s;
s=" "+s;
int i=1,j=n;
int cnt=0;
while (i<=j){
if (s[i]=='2'&&s[j]=='5'){
swap(s[i],s[j]);
cnt++;
}
if (s[i]=='2') j--;
else i++;
}
cout<<cnt;
}
双指针,前后扫描,如果后指针 \(j\) 为 \(5\) 且前指针 \(i\) 为 \(2\) ,说明这样会形成 \(25\) 子序列,需要交换这两个元素
这样操作的次数一定是最小的,因为我们要保证所有的 $2 $ 都在 \(5\) 的后面,才不会出现 \(25\) 子序列
C:
题目大意:给出两个元素个数都为 \(n\) 的数组 \(a,b\) ,记数组 \(c_i=a_i\times b_i\times i\) ,对 \(b\) 重新排序后使得 \(c\) 数组元素和最大,输出排序后的序列
LL a[200010],b[200010];
pair<LL,int> c[200010];
LL ans[200010];
void solve(){
int n;
cin>>n;
for (int i=1;i<=n;i++) cin>>a[i];
for (int i=1;i<=n;i++) cin>>b[i];
for (int i=1;i<=n;i++) a[i]*=i;
for (int i=1;i<=n;i++) c[i]={a[i],i};//存下标
sort(c+1,c+n+1);
sort(b+1,b+n+1);
for(int i=1;i<=n;i++) ans[c[i].second]=b[i];//配对
for (int i=1;i<=n;i++) cout<<ans[i]<<' ';
}
\(c_i=a_i\times b_i\times i\) 中,可以固定的成分是 \(a_i\times i\) ,为了使 \(c\) 的元素和最大,可以贪心的将较大的 \(b_i\) 和较大的 \(a_i\times i\) 相匹配
对 \(a_i \times i\) 进行排序时同时记录下标的位置,最后令从小到大排序后 \(b\) 与同样从小到大排序后的 \(a_i\times i\) 进行配对
利用记录的下标信息存储 \(b_i\) 对应的位置,最后输出
D:
题目大意:
string s[200010];
LL n,k;
bool judge(LL mid){
LL res=1;
LL cnt2=0,sum=0;
for (int i=1;i<=n;i++){
for (int j=0;j<s[i].size();j++){
if (s[i][j]=='2') cnt2++;
if (s[i][j]=='5') sum+=cnt2;
if (sum>mid){
cnt2=0,sum=0;
res++,i--;
if (res>k) return 1;
break;
}
}
}
return 0;
}
void solve(){
cin>>n>>k;
string S;
for (int i=1;i<=n;i++)
cin>>s[i];
LL l=-1,r=LLinf;
while(l+1!=r){
LL mid=l+r>>1;
if (judge(mid))
l=mid;
else
r=mid;
}
cout<<r;
}
想到了二分,结果卡 long long 褒姒了
最大化最小值,可以二分 \(25\) 子序列个数,然后对每个二分值都用线性DP的方式验证是否满足子区间个数小于等于 \(k\)
时间复杂度为 \(O(n\log n)\)
for (int i=1;i<=n;i++){
for (int j=0;j<s[i].size();j++){
if (s[i][j]=='2') cnt2++;
if (s[i][j]=='5') sum+=cnt2;
if (sum>mid){
cnt2=0,sum=0;
res++,i--;
if (res>k) return 1;
break;
}
}
}
第一层循环枚举每个数字 \(a_i\) ,第二次循环处理 \(a_i\) 中的每位元素,这里用 string 存数字方便操作
如果枚举 \(a_i\) 时,发现当前区间中的 \(25\) 子序列个数超过传入的二分值,那么这个区间就在 \(a_i\) 前中断
从 \(a_i\) 开始考虑下一个区间,所以需要回退 \(i\) ,\(res\) 记录当前的区间个数,如果在这时的 \(res\) 已经超过了 \(k\) ,立即剪枝返回
E:
题目大意:
int dg[200010];
LL a[200010];
void solve(){
int n;
cin>>n;
LL mn=1e9+1;
for (int i=1;i<=n;i++){
cin>>a[i];
mn=min(mn,a[i]);
}
for (int i=1;i<n;i++){
int u,v;
cin>>u>>v;
dg[u]++;
dg[v]++;
}
if (n==1){
cout<<2*mn;
return ;
}
LL sum=0;
int cnt=0;
for (int i=1;i<=n;i++)
if (dg[i]==1) sum+=a[i],cnt++;
if (cnt%2) sum+=mn;
cout<<sum;
}
诈骗题,手玩几组样例可以得到结论
选择两个未染色的叶子节点进行操作一定优
简单证明:
假设存在一条链:
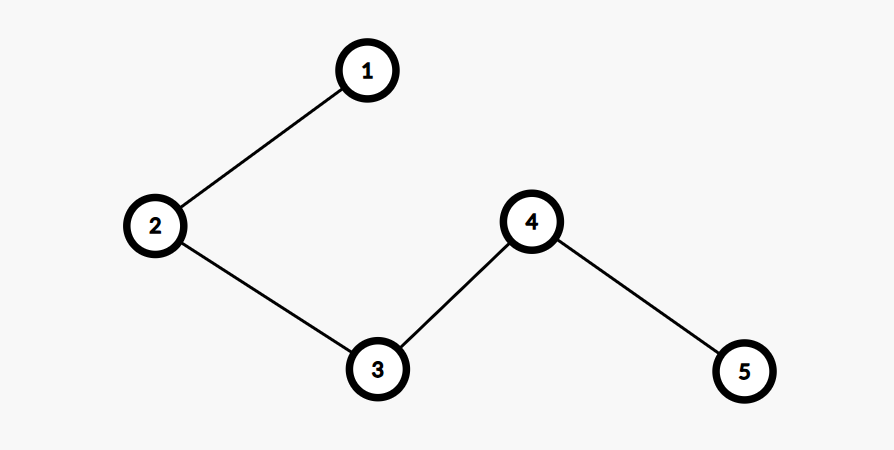
首先证明使得链上所有节点全被染色的最优方案是选择首位两个节点进行操作二
选择上图中的 \(1\) 和 \(5\) 路径为 \((1,5)\),总代价为 \(a_1+a_5\),如果存在另外一种方案使得他们路径上的点都被染色,例如选择路径 \((1,3),(4,5)\) 这样的方案的代价为 \(a_1+a_3+a_4+a_5\) ,显然大于 \(a_1+a_5\)
现在考虑普通树上的问题:
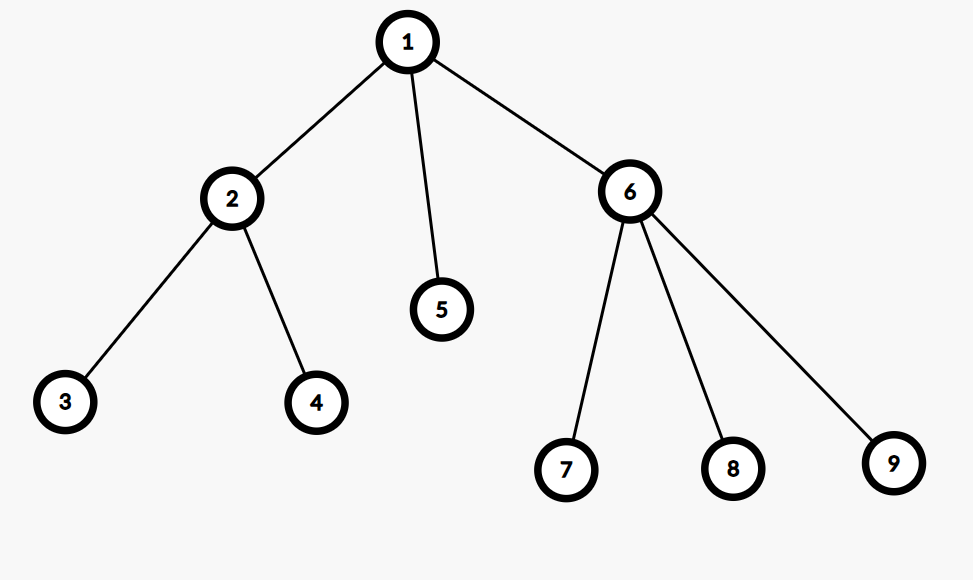
可以将树拆分为多个长链,首位都是叶子节点,所以对树的最优染色操作就是每次选取两个未染色的叶子节点,做操作二
但这里存在一个问题,因为每次都需要选取两个没有染色的叶子节点,当叶子节点数为奇数时,需要特殊考虑
剩余的最后一个叶子节点 \(a_x\) 可以和任意一个节点做操作二,甚至可以选自己做操作一
那么总代价为 \(a_x+a_y\) ,要使得 \(a_y\) 最小,可以取树上最小代价的点做操作二,如果这个点是他本身,那么操作一和二没有区别
所以总代价最小为所有叶子节点的代价和加上叶子节点为偶数时的特殊代价
可能会存在这样的疑惑:
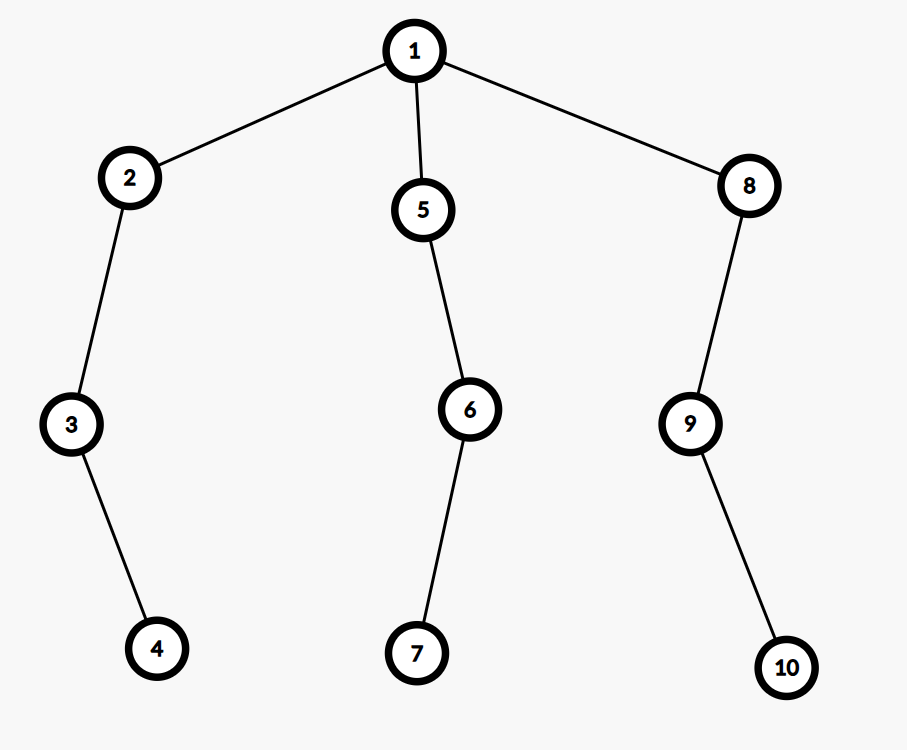
如果选了路径 \((4,10)\) ,剩下节点 \(5,6,7\) 还没有染色,这时考虑叶子节点数为奇数的特殊情况,如果这棵树上代价最小的点为 \(6\) ,
那么根据上面的结论选取 \((6,7)\) 这个路径染色会漏掉节点 \(5\),是否结论错误?
其实不然,第一次可以不取 \((4,10)\) 而是取 \((7,10)\) ,那么最后的特殊情况就会选取路径 \((4,6)\) 从而覆盖所有节点
同理第一次 \((4,7)\) 特殊情况取路径 \((6,10)\) 同样可以覆盖所有节点,并且这两种染色方案的总代价都是最优的
说明最优解和取的路径无关,如果能找到最小代价,那么就一定存在对应的染色方案
F:
题目大意:
pair<int,int> a[200010];
int p[200010];
int mem[200010];
int ans[200010];
void solve(){
int n;
cin>>n;
for (int i=1;i<=n;i++) cin>>a[i].first,a[i].second=i;
for (int i=1;i<=n;i++)
p[i]=pow(2,(int)log2(i+1)+1)-1;
sort(a+1,a+n+1);;
for (int i=n;i>=1;i--){
if (mem[a[i].first])
ans[a[i].second]=mem[a[i].first];
else{
ans[a[i].second]=a[i].first^p[a[i].first];
mem[a[i].first^p[a[i].first]]=a[i].first;
}
}
for (int i=1;i<=n;i++) cout<<ans[i]<<' ';
}
构造题,这次对上了脑电波,观察到题目给出的 \(n\) 为偶数,猜到 \(a_i,b_i\) 可以两两配对
给出 \([1,10]\) 的二进制表示:
0001 1
0010 2
0011 3
0100 4
0101 5
0110 6
0111 7
1000 8
1001 9
1010 10
因为需要让 \(a_i\oplus b_i\) 最大,那么对于 \(a_i,b_i\) 有更多的位次不同,那么异或值一定更大
所以在相同情况下 \(1010_2\oplus 0101_2>0101_2\oplus 0010_2\)
又可以发现,在 \([1,10]\) 中所有的元素都可以最优匹配,即在同一位上可以找到相反的元素,例如
1010 10
0101 5
1001 9
0110 6
1000 8
0111 7
0100 4
0011 3
0010 2
0001 1
从大到小匹配下来可以知道所有的 \(a_i,b_i\) 在排列下都可以一一匹配,且这样的贪心匹配方式满足了最优性
那么问题可以转化为如何和找到 \(a_i\) 匹配的 \(b_i\) :
可以找到大于 \(a_i\) 的最小的 \(2\) 的次方数,将 \(a_i \oplus 2^n-1\) 得到对应的 \(b_i\),\(2^n-1\) 的数位全为 \(1\)
for (int i=1;i<=n;i++)
p[i]=pow(2,(int)log2(i+1)+1)-1;
例如 \(a_i=10=1010_2\) ,那么 \(2^n=16,2^n-1=15=1111_2\),计算 \(1111_2\oplus 1010_2=0101_2=5\)
形象化的,对于 \(a_i\) 设他的最高 \(1\) 数位是 \(x\),我们需要得到在同一数位 \(x\) 下所有的数位都为 \(1\) 的数
if (mem[a[i].first])
ans[a[i].second]=mem[a[i].first];
else{
ans[a[i].second]=a[i].first^p[a[i].first];
mem[a[i].first^p[a[i].first]]=a[i].first;
}
用 mem 数组记录当前配对的 \(a_i,b_i\) ,如果在倒序枚举时遇到了之前已经匹配过的对,那么直接输出对应的值即可
例如 \((10,5)\) 已经配对,那么在枚举到 \(5\) 时,就不用向下找 \(5\) 对应数,而是直接输出 \(10\)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号