树的重心与直径

树的重心与直径

树的重心

有以下三种定义方式：

• 以某点为根，最大子树的节点数最小，该点为重心
• 以某点为根，所有子树的节点数不超过总节点数的一半，该点为重心
• 以某点为根，所有节点到这个根边数和最小，该点为重心

也存在以下这些性质：

• 一棵树最多有两个重心，且这两个重心一定相邻
• 给这棵树增加或减少一个叶子节点，转移后的重心最多只会移动一条边
• 将两棵树合并后，新的重心一定在原来的两个重心的路径上
• 如果树的边权都为正，那么所有节点到重心的边权和最小，且与边权的分布无关

---

求树的重心，可用树形DP的方式计算

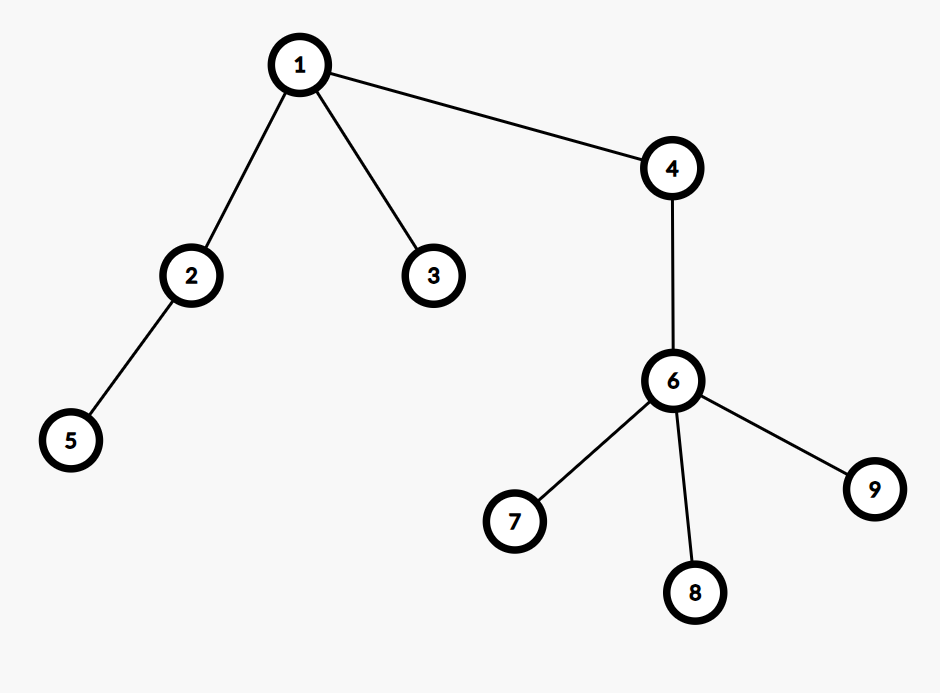
计算重心的过程中，任取当前遍历到的节点 \(u\)，如果 \(u\) 为重心，那么可以把以 \(u\) 为根的子树连通块分为两类：

\(u\) 的子树和 \(u\) 之上的连通块，例如在上图中以 \(6\) 为根节点，则第一类为连通块 \(\{1,2,3,4,5\}\) 第二类为 \(\{7\},\{8\},\{9\}\)

根据树的重心的第一个定义，我们需要使得 \(u\) 节点的最大子树的节点数与 \(u\) 节点之上的连通块的节点数的最大值最小

设 \(sum\) 以 \(u\) 节点为根的子树的节点数之和，\(size\) 为 \(u\) 节点最大子树的节点树

那么 \(u\) 之上的连通块的节点数为 \(n-size\)，\(n\) 为所有节点总数，我们需要使这样一个表达式最小，即计算：

\[{\rm{min}_{u=1}^n}[{\rm{max}}(size_u,n-sum_u)] \]

int dfs(int x,int p){
	int size=0;//初始化
	int sum=1;//以u为根的节点总数包括根节点
	for (auto v:e[x]){
		if (v==p) continue;
		int res=dfs(v,x);//
		size=max(size,res);//回溯计算最大子树的节点数
		sum+=res;//回溯计算以u为根的节点总数
	}
	if (ans>max(size,n-sum)){
		ans=max(size,n-sum);
		st.clear();
		st.push_back(x);
	}else if (ans==max(size,n-sum))
		st.push_back(x);//如果有多个重心则记录
	return sum;//返回以这个节点为根的节点总数
}

每次回溯时，都上传 \(sum\) ，即向父节点转移以某个子节点 \(u\) 为根的节点总数

同时在父节点上计算他的最大子树的节点数，即 size=max(size,dfs(v,x))

树的直径

定义：树上任意两点之间最长的简单路径为树的直径

有两种求法为：两次DFS，树形DP

其中 DFS 的方法只能处理非负权树，树形DP的方法无法得到直径路径上的信息（只能得到直径的值）

存在以下性质：

• 直径两端点一定是两个叶子节点
• 对于两棵树，他们的直径分别被表示为 \({\rm{dis}}(x,y),{\rm{dis}}(u,v)\) ，用一条边将这两棵树连接后新树的直径一定是 \(\{x,y,u,v\}\) 其中的两个点形成的简单路径
• 对于一棵树的，在他的某一点上新接一个叶子节点，那么最多只会改变树的直径的一个端点
• 如果一棵树有多个直径，那么这些直径一定会有一部分在中间部分重合 （公共点或公共路径）

---

两次DFS：

第一次DFS找到离出发点最远的节点 \(c\) ，第二次DFS从 \(c\) 出发再到离 \(c\) 最远的节点，他们之间的简单路径距离即为树的直径

void dfs(int x,int p){
	for (auto it:e[x]){
		if (it.v==p) continue;
		d[it.v]=d[x]+it.w;//记录路径长度
		if (d[it.v]>d[c]) c=it.v;//更新最远点
		dfs(it.v,x);
	}
}

void solve(){
	int n;
	cin>>n;
	for (int i=1;i<n;i++){
		int u,v,w;
		cin>>u>>v>>w;
		e[u].push_back({v,w});
		e[v].push_back({u,w});
	}
	dfs(1,-1);
	d[c]=0;//第二次dfs从c出发
	dfs(c,-1);
	cout<<d[c]<<endl;
}

---

树形DP：

任取树上一点 \(u\) ，\(d_1,d_2\) 分别记录 \(u\) 的子树中的最长路径和次长路径，需要计算的树的直径为 \({\rm{max}_{u=1}^n}(d_{1}+d_2)\)

int dfs(int x,int p){
	int d1=0;
	int d2=0;
	for (auto it:e[x]){
		if (it.v==p) continue;
		int td=dfs(it.v,x)+it.w;//计算子节点的最远路径
		if (td>d1) d2=d1,d1=td;//更新最长路径和次长路径
		else if (td>d2) d2=td;
		ans=max(ans,d1+d2);//记录答案
	}
	return d1;//返回当前节点的最长路径
}


void solve(){
	int n;
	cin>>n;
	for (int i=1;i<n;i++){
		int u,v,w;
		cin>>u>>v>>w;
		e[u].push_back({v,w});
		e[v].push_back({u,w});
	}
	int x=dfs(1,-1);
	cout<<ans;
}