牛客 周赛88 20250410
牛客 周赛88 20250410
https://ac.nowcoder.com/acm/contest/106318
A:
题目大意:
void solve(){
int a,b,c;
cin>>a>>b>>c;
if (c>=a*b) cout<<"YES";
else cout<<"NO";
}
签到
B:
题目大意:给定三角形的三个点的整数坐标,判断是否存在一条中线与坐标轴重合
void solve(){
int xa,xb,xc,ya,yb,yc;
cin>>xa>>ya>>xb>>yb>>xc>>yc;
if ((ya+yb==0&&yc==0)||(yc+ya==0&&yb==0)||(yc+yb==0&&ya==0)||
(xa+xb==0&&xc==0)||(xb+xc==0&&xa==0)||(xa+xc==0&&xb==0))
cout<<"YES"<<endl;
else
cout<<"NO"<<endl;
}
忘了中线定义WA三发,在三角形中,连接一个顶点与对边中点的线段称为该顶点的中线
C:
题目大意:给定三角形的三个点的整数坐标,判断是否存在一条中线与坐标轴平行
void solve(){
double xa,xb,xc,ya,yb,yc;
cin>>xa>>ya>>xb>>yb>>xc>>yc;
if (((ya+yb)/2==yc)||((yb+yc)/2==ya)||((ya+yc)/2==yb)||
((xa+xb)/2==xc)||((xb+xc)/2==xa)||((xa+xc)/2==xb))
cout<<"YES"<<endl;
else
cout<<"NO"<<endl;
}
简单模拟
D:
题目大意:给定 \(x\) 判断是否存在 \(1\le z<x\) 使得 \((x,x+z)\) 构成一个合法对,定义合法对 \((x,y)\) 为当且仅当 \(x\) 的二进制为 \(1\) 的数位在 \(y\) 中也为 \(1\)
int lg[32];
void init(){
lg[0]=1;
for (int i=1;i<32;i++)
lg[i]=lg[i-1]*2;
for (int i=0;i<32;i++)
lg[i]--;
}//预处理全1数位
void solve(){
int x;
cin>>x;
for (int i=0;i<32;i++){
if(x==lg[i]){
cout<<-1<<endl;
return ;
}
}
int b=1;
while(x&1){
x>>=1;
b<<=1;
}//将1定位到x的第一个0位
cout<<b<<endl;
}
特殊情况,因为 \(1\le z<x\) ,所以当 \(x\) 的二进制全为 \(1\) 时,无解
然后贪心考虑 \(z\) 有且仅有一个数位为 \(1\) ,并且刚好使得 \(x+z\) 是 \(x\) 的超集, 所以只需要从最低位开始找 \(x\) 的第一个是 \(0\) 的数位
构造 \(z\) 在这个数位上为 \(1\) 其他数位填充 \(0\) ,那么可以保证 \((x+z)\oplus z\ne0\)
E:
题目大意:

LL dp[200010][2];
void solve(){
int n,k;
cin>>n>>k;
vector<LL> a(n+1),b(n+1);
for (int i=1;i<=n;i++) cin>>a[i];
for (int i=1;i<=n;i++) cin>>b[i];
memset(dp,-0x3f,sizeof dp);
dp[1][0]=a[1];
for (int i=2;i<=n;i++){
dp[i][0]=dp[i-1][0]+a[i];
dp[i][1]=dp[i-1][1]+b[i];
if (dp[i-1][0]>=k)
dp[i][1]=max(dp[i-1][0]-k+b[i],dp[i][1]);
if (dp[i-1][1]>=k)
dp[i][0]=max(dp[i-1][1]-k+a[i],dp[i][0]);
}
cout<<max(dp[n][1],dp[n][0]);
}
这题一开始只有 \(75\%\) 的分,原因在于没有将 \(dp\) 初始化为一个极小值代表该点不可达
考虑 \(dp_{i,j}\) 表示走到第 \(i\) 号点的 \(j\) 世界时的最大金币数,状态转移为
走到 \(i\) 号点的状态由上一个点转移而来,如果上一个点不转换世界,仍然继续向后递推
dp[i][0]=dp[i-1][0]+a[i];
dp[i][1]=dp[i-1][1]+b[i];
如果上个点可以转换世界,那么判断转移后的最优解
if (dp[i-1][0]>=k)
dp[i][1]=max(dp[i-1][0]-k+b[i],dp[i][1]);
if (dp[i-1][1]>=k)
dp[i][0]=max(dp[i-1][1]-k+a[i],dp[i][0]);
F:
题目大意:

void solve(){
int n;
cin>>n;
vector<int> a(n+2);
for (int i=1;i<=n;i++) cin>>a[i];
a[n+1]=1;
vector<int> ans;
int st=1;
for (int i=1;i<=n+1;i++){
if (a[i]!=0){
for (int j=i-1;j>=1;j--)
ans.push_back(a[i]+j);
st=i;
break;
}
}
int cnt=0;
for (int i=st;i<=n;i++){
if (a[i]==0)
cnt++;
if (a[i]!=0){
if (ans.empty()){
ans.push_back(a[i]);
continue;
}
if (abs(a[i]-ans.back())>cnt+1||(cnt-abs(a[i]-ans.back()))%2==0){
cout<<-1<<endl;
return;
}
while (cnt){
if (ans.back()<=a[i])
ans.push_back(ans.back()+1);
else
ans.push_back(ans.back()-1);
cnt--;
}
ans.push_back(a[i]);
}
}
while (cnt--)
ans.push_back(ans.back()+1);
for (auto it:ans) cout<<it<<' ';
}
考码力的大模拟,特殊情况比较多
int st=1;
for (int i=1;i<=n+1;i++){
if (a[i]!=0){
for (int j=i-1;j>=1;j--)
ans.push_back(a[i]+j);//向前填充
st=i;
break;
}
}
首先是前面都是连续 \(0\) 的特殊情况,需要找到数组中第一个不为 \(0\) 的元素,然后向前填充依次 \(+1\)
然后是普遍情况,在两个不为 \(0\) 的元素之间有连续的 \(0\) ,我们每次将不为 \(0\) 的元素装入 ans
如果为当前走到的元素为 \(0\),那么记录这一段连续的 \(0\) 的个数,到下一个不为 \(0\) 的元素为止
if (abs(a[i]-ans.back())>cnt+1||(cnt-abs(a[i]-ans.back()))%2==0){
cout<<-1<<endl;
return;
}
考虑无解的情况,我们需要保证相邻元素之差为 \(1\),设 \(a,b\) 且 \(a<b\) 之间有连续的 \(n\) 个 \(0\)
显然当 \(b-a>n+1\) 时无解,填充的元素依次递增也连接不上 \(a,b\)
然后是手玩出来的结论,当 \(n-(b-a)\%2=0\) 时也无解,可以带入数据验证,例如
1 0 0 0 0 1
最优填充方案为
1 2 1 2 1 1
明显连接不上
排除无解的情况后现在需要构造有解的 ans
while (cnt){
if (ans.back()<=a[i])
ans.push_back(ans.back()+1);
else
ans.push_back(ans.back()-1);
cnt--;
}
如果当前的结尾元素小于等于需要连接到的元素,那么就构造一个向上加一的元素
如果当前的结尾元素大于需要连接到的元素,那么就构造一个向下减一的元素
小于等于构造加一的原因是当数组为 1 0 1 时,我们不能不做修改,所以至少要加一
然后是结尾的特殊情况,结尾段全为 \(0\) ,这时我们的 cnt 仍然记录着需要构造的元素个数,那么显然从 ans 尾部一直向后 \(+1\) 构造最简单
while (cnt--)
ans.push_back(ans.back()+1);
最后的一种特殊情况,当数组全 \(0\) 时,可以在最后增设一个元素 \(a_{n+1}=1\) ,使得这种特殊情况能够通过 前面都是连续 \(0\) 的情况构造出来
G:
题目大意:

LL a[200010];
vector<int> e[200010];
LL sonmx[200010],lc[200010],rc[200010],lf[200010],pre[200010],fa[200010];
LL premx[200010],sufmx[200010],mp[200010];
int idx=1;
LL dfs(int x){
pre[x]=pre[fa[x]]+a[x];
lc[x]=rc[x]=x;
if (e[x].empty()){
mp[x]=idx;
lf[idx]=x;
idx++;
return sonmx[x]=a[x];
}
for (auto v:e[x])
sonmx[x]=max(sonmx[x],dfs(v));
lc[x]=lc[e[x].front()];
rc[x]=rc[e[x].back()];
sonmx[x]+=a[x];
return sonmx[x];
}
void init(){
dfs(1);
memset(premx,-0x3f,sizeof premx);
memset(sufmx,-0x3f,sizeof sufmx);
for (int i=1;i<idx;i++)
premx[i]=max(premx[i-1],pre[lf[i]]);
for (int i=idx-1;i>=1;i--)
sufmx[i]=max(sufmx[i+1],pre[lf[i]]);
}
void solve(){
int n,q;
cin>>n>>q;
for (int i=1;i<=n;i++) cin>>a[i];
for (int i=2;i<=n;i++){
int p;
cin>>p;
fa[i]=p;
e[p].push_back(i);
}
init();
while (q--){
LL x,y;
cin>>x>>y;
LL l=mp[lc[x]],r=mp[rc[x]];
LL ans=max(premx[l-1],sufmx[r+1]);
ans=max(ans,pre[fa[x]]);
ans=max(ans,pre[y]+sonmx[x]);
cout<<ans<<endl;
}
}
超级难写的类似树链剖分的题,需要预处理一大堆东西
对于样例给出的树
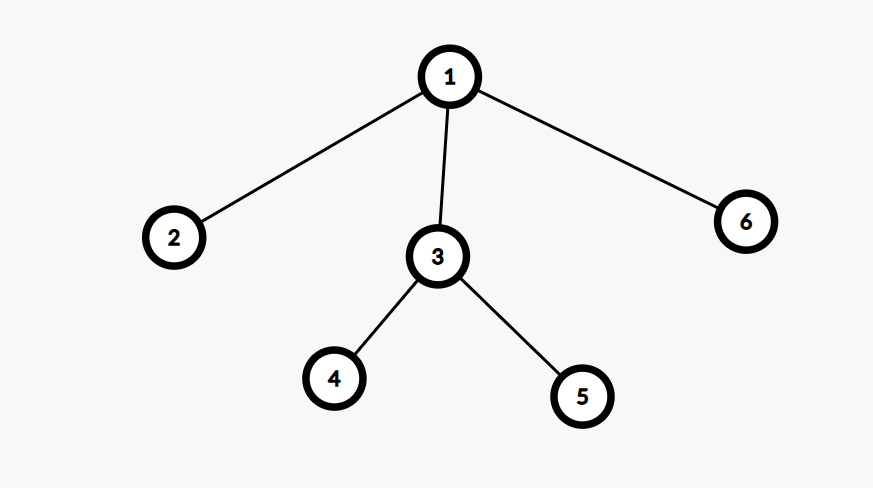
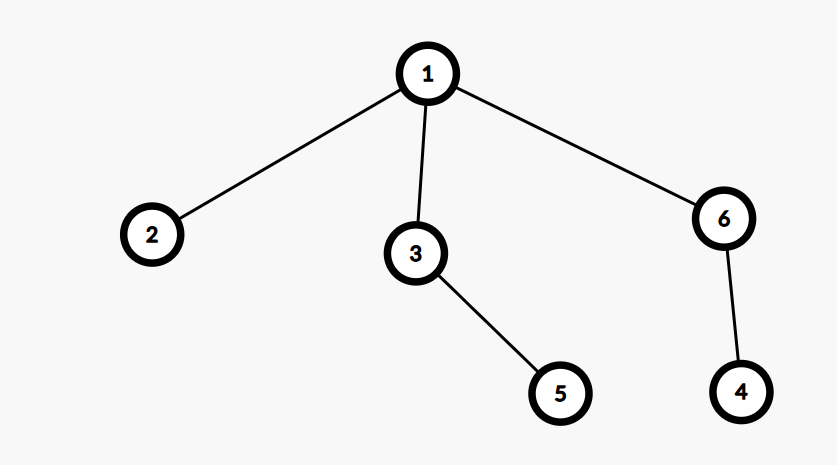
询问中的树为
题目定义的树的价值为所有叶子节点到根节点简单路径的权值之和的最大值
在原树中,按照从左到右的顺序,叶子节点的价值分别为 \(12,13,7,3\),那么整棵树的价值为 \(13\)
询问将 \(4\) 节点断开与 \(6\) 节点连接后的树的价值,考虑断开后叶子节点价值的变化,从左到右为 \(12,7,3+7\)
将所有叶子节点看做一段排列连续的元素,断开节点的所有叶子节点为一段区间 \([l,r]\),将这段区间接到另外的节点上
那么树的价值被重新表示为区间 \([1,l-1],{\rm{oldleaf'father}},[r+1,n],{\rm{newleaf}}\)
其中 \({\rm{oldleaf'father}}\) 为断开节点父亲的价值,这是因为这个父亲有可能单独形成一个叶子节点,比如

将图中的 \(4\) 断开,那么会新生成一个叶子节点 \(2\)
其中 \({\rm{newleaf}}\) 为断开节点的所有叶子节点在接上新的父亲后的区间最大值 ,那么这段区间的最大价值为断开节点的最大价值加上所接父亲的价值
所以需要对每个节点维护这些信息
LL sonmx[200010],lc[200010],rc[200010],pre[200010],fa[200010];
//所管辖的叶子的最大价值,所管辖的叶子节点的左区间编号,所管辖的叶子节点的右区间编号
//树上前缀和计算的该节点的价值,节点的父亲
然后类似于树链剖分的思想,将所有的叶子节点维护在一段连续的区间上,从 \(1\) 开始标号,表示从左数的第 \(i\) 个叶子节点
LL dfs(int x){
pre[x]=pre[fa[x]]+a[x];//计算节点价值
lc[x]=rc[x]=x;/
if (e[x].empty()){
mp[x]=idx;//存叶子节点对应的虚拟标号
lf[idx]=x;//存虚拟区间标号对应的树上编号
idx++;
return sonmx[x]=a[x];//叶子节点所管辖的叶子的最大价值是他本身
}
for (auto v:e[x])
sonmx[x]=max(sonmx[x],dfs(v));
lc[x]=lc[e[x].front()];//计算所管辖的叶子节点的左区间树上编号
rc[x]=rc[e[x].back()];//利用给定的边抽象构造树的结构,左右区间通过边的顺序确定
sonmx[x]+=a[x];//计算非叶子节点所管辖的叶子的最大价值
return sonmx[x];
}
然后考虑维护叶子节点的虚拟标号下的前缀和后缀最大值
for (int i=1;i<idx;i++)
premx[i]=max(premx[i-1],pre[lf[i]]);
for (int i=idx-1;i>=1;i--)
sufmx[i]=max(sufmx[i+1],pre[lf[i]]);
最后实现 \(O(1)\) 询问的回答
cin>>x>>y;
LL l=mp[lc[x]],r=mp[rc[x]];//断开节点所管辖的叶子节点对应树上编号->虚拟标号的区间
LL ans=max(premx[l-1],sufmx[r+1]);
ans=max(ans,pre[fa[x]]);
ans=max(ans,pre[y]+sonmx[x]);//综合四个区间的最值得到答案
cout<<ans<<endl;



 浙公网安备 33010602011771号
浙公网安备 33010602011771号