2025CDUT蓝桥杯模拟赛
2025CDUT蓝桥杯模拟赛
https://ac.nowcoder.com/acm/contest/106665
A：
前缀和（写得好的暴力也能过）
const int N=1e6+10;
LL p[N];
void init(){
for (int i=1;i<=N;i++){
int j=i;
int a=0;
while (j){
if (j%10==4||j%10==6||j%10==9||j%10==0)
a+=1;
if (j%10==8)
a+=2;
j/=10;
}
p[i]=p[i-1]+a;
}
}
void solve(){
int a,b;
cin>>a>>b;
cout<<p[b]-p[a-1]<<endl;
}
B：
是一道比较简单的搜索题，这里给出两种写法
题目要求只需要判断是否存在到达终点的路径，所以DFS可以不用回溯，如果能到终点那么就连锁回退
其实BFS比DFS好写一点（
int n,m;
char g[510][510];
bool vis[510][510];
int dx[]={1,0,-1,0};
int dy[]={0,1,0,-1};
bool dfs(int x,int y){
if (g[x][y]=='t') return 1;
vis[x][y]=1;
for (int i=0;i<4;i++){
int tx=x+dx[i],ty=y+dy[i];
if (tx<1||ty<1||tx>n||ty>m) continue;
if (vis[tx][ty]==1||g[tx][ty]=='x') continue;
if (dfs(tx,ty)) return 1;
}
return 0;
}
void solve(){
cin>>n>>m;
for (int i=1;i<=n;i++)
for (int j=1;j<=m;j++)
cin>>g[i][j];
memset(vis,0,sizeof vis);
for (int i=1;i<=n;i++){
for (int j=1;j<=m;j++){
if (g[i][j]=='s'){
if (dfs(i,j))
cout<<"YES"<<endl;
else
cout<<"NO"<<endl;
}
}
}
}
BFS：
bool bfs(int x,int y){
queue<pair<int,int>> q;
q.push({x,y});
while (q.size()){
auto t=q.front();
q.pop();
if (vis[t.first][t.second]) continue;
vis[t.first][t.second]=1;
for (int i=0;i<4;i++){
int tx=t.first+dx[i],ty=t.second+dy[i];
if (tx<1||ty<1||tx>n||ty>m) continue;
if (g[tx][ty]=='x') continue;
if (g[tx][ty]=='t') return 1;
if (g[tx][ty]=='.') q.push({tx,ty});
}
}
return 0;
}
void solve(){
memset(vis,0,sizeof vis);
cin>>n>>m;
for (int i=1;i<=n;i++)
for (int j=1;j<=m;j++)
cin>>g[i][j];
for (int i=1;i<=n;i++){
for (int j=1;j<=m;j++){
if (g[i][j]=='s'){
if (bfs(i,j))
cout<<"YES"<<endl;
else
cout<<"NO"<<endl;
}
}
}
}
C：
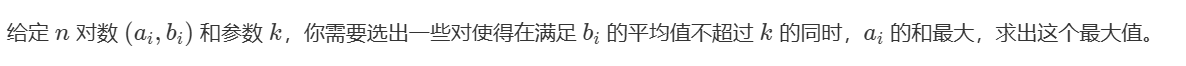
小于平均值的 \(b_i\) 放进去一定优，所以一定要放
然后我们需要让大于平均值的物品放进背包，考虑这样一个问题，记小于平均值的 \(b_i\) 为 \(x_i\) ，大于平均值的 \(b_i\) 为 \(y_i\)
\[\frac{\sum x_i+\sum y_j}{\sum (i+j)} \le k
\]
其中我们已经贪心的计算出了 \(\sum x_i\) ，那么剩下的信息可以构成一个01背包的问题
背包的容量为 \(\sum (k-x_i)\) ，并且此时已经有小于平均值的物品的价值放进去了
所以题目转化为在容量 \(\sum (k-x_i)\) 的背包下，求剩下大于平均值的物品放进背包的最大价值为多少
vector<pair<int,int>> ob;
int dp[250010];
void solve(){
int n,k;
cin>>n>>k;
int v=0,sum=0;
for (int i=1;i<=n;i++){
int a,b;
cin>>a>>b;
if (b<=k){
v+=k-b;
sum+=a;
}else
ob.push_back({a,b-k});
}
for (auto it:ob)
for (int j=v;j>=it.second;j--)
dp[j]=max(dp[j],dp[j-it.second]+it.first);
cout<<dp[v]+sum;
}
D：
\[\sum_i \lvert A_i+x\rvert +\sum_i \lvert B_i-x\rvert+\lvert x\rvert
\]
这个函数是关于 \(x\) 的一个下凹函数，最小值对应的 \(x\) 是集合 \(\{-A\}+B+0\) 的中位数
简单证明：
\[ \sum_i \lvert A_i+x\rvert +\sum_i \lvert B_i-x\rvert+\lvert x\rvert
\]
\[ \implies \sum_i \lvert x-(-A_i)\rvert +\sum_i \lvert x-B_i\rvert+\lvert x-0\rvert
\]
\[ \implies \sum_i \lvert x-C_i\rvert\ C=\{-A\}+B+0
\]
中位数对于绝对值函数的最优解我们这里不做更多解释
void solve(){
int n,m;
cin>>n>>m;
vector<LL> a(n+1),b(m+1),x;
for (int i=1;i<=n;i++) cin>>a[i];
for (int i=1;i<=m;i++) cin>>b[i];
for (int i=1;i<=n;i++) x.push_back(-a[i]);
for (int i=1;i<=m;i++) x.push_back(b[i]);
x.push_back(0);
sort(x.begin(),x.end());
LL mid=x[x.size()/2];
LL sum=abs(mid);
for (int i=1;i<=n;i++) sum+=abs(a[i]+mid);
for (int i=1;i<=m;i++) sum+=abs(b[i]-mid);
cout<<sum;
}
E：
对于一个字符串，由于字典序是先由前面元素决定，我们应当首先让位置靠前的可以使字典序变小的位置被复制
然后考虑代价，就有从前往后贪心，取字符进行复制，如果目前的总灵力可以取这个位置那就取
注意数据范围
void solve(){
LL n,m;
string s;
cin>>n>>m;
cin>>s;
s=" "+s;//下标从1开始
vector<LL> a(n+1);
for (int i=1;i<=n;i++) cin>>a[i];
vector<pair<LL,int>> vp;//记录当前可以复制的子串序列
vp.push_back({a[1],1});
set<int> st;//记录能够复制字符的位置
auto judge=[&](){
sort(vp.begin(),vp.end());//对子串序列中的元素按照代价从小到大排序
for (auto it:vp){//枚举
if (m-it.first>=0){//如果可以复制
m-=it.first;
st.insert(it.second);//记录位置
}
else
break;//退出
}
};
for (int i=2;i<=n;i++){
if (s[i]>s[i-1]){//如果当前s[i]比上一个s[i-1]大
judge();//选取字符进行复制
vp.clear();//清空
vp.push_back({a[i],i});
}
if (s[i]<s[i-1]){
vp.clear();//当前s[i]比上一个s[i-1]小，复制s[i]一定比复制s[i-1]之前的更优
vp.push_back({a[i],i});
}
if (s[i]==s[i-1]){
vp.push_back({a[i],i});
}
}
for (int i=1;i<=n;i++){
if (st.count(i)) cout<<s[i]<<s[i];//如果是在记录复制的位置上，那么多输出一个
else cout<<s[i];
}
}
F：
定义 \(dp_i\) 表示抓鼹鼠序列以第 \(i\) 只鼹鼠结尾能抓的最大数量，显然的对任意 \(dp_i\) 都初始化为 \(1\)
考虑状态的转移，第 \(i\) 只鼹鼠只能从之前能走到的鼹鼠 \(j\) 转移
\[dp_i=dp_j+1
\]
如果能转移，说明他们之间的曼哈顿距离小于他们的时间差
\[\lvert x_i-x_j\rvert +\lvert y_i-y_j\rvert\le t_i-t_j
\]
struct node{
int x,y,t;
};
node p[10010];
int dp[10010];
void solve(){
int n,m;
cin>>n>>m;
for (int i=1;i<=m;i++)
cin>>p[i].t>>p[i].x>>p[i].y;
int ans=0;
for (int i=1;i<=m;i++){
dp[i]=1;
for (int j=1;j<i;j++){
if (abs(p[i].x-p[j].x)+abs(p[i].y-p[j].y)<=p[i].t-p[j].t)
dp[i]=max(dp[i],dp[j]+1);
}
ans=max(ans,dp[i]);
}
cout<<ans;
}
G：
并查集， \(1e18\) 拆成二进制的 \(64\) 位，对每一位上的 \(1\) 都设计一个虚拟集合
即
00...001
00...010
...
01...000
10...000
考虑将 \(w_i\) 按位拆解，与对应位都有 \(1\) 的虚拟集合进行并查集的合并
const int N=1e5;
int cnt[N+100];
int fa[N+100];
int find(int x){
if (fa[x]==x) return x;
else return fa[x]=find(fa[x]);
}
void merge(int x,int y){
int fx=find(x),fy=find(y);
if (fx!=fy){
fa[fx]=fy;
cnt[fy]+=cnt[fx];//记录节点数
}
}
void solve(void){
int n;
cin>>n;
for (int i=1;i<=100000;i++) fa[i]=i;
for (int i=n+1;i<=n+64;i++) cnt[i]=0;//将n之后节点放出64个来存储虚拟节点
for (int i=1;i<=n;i++) cnt[i]=1;
for (int i=1;i<=n;i++){
long long t;
cin>>t;
for (int j=0;j<64;j++){
if (t>>j&1)//按位拆解合并
merge(i,n+1+j);
}
}
int ans=0;
for (int i=n+1;i<=n+64;i++) ans=max(ans,cnt[i]);
cout<<ans<<endl;
}
H：
原原又板板啊，分层图最短路模板
对每个加入队列的元素都记录状态，包括到起点的距离、编号、所用免费次数
struct edge{
int v,w;
};
struct ste{
int d,num,cnt;
bool operator<(const ste& a)const {
return d>a.d;
}//优先队列重载小于号
};
vector<edge> e[10010];
int n,m,k,s,t;
int dis[10010][12];
bool vis[10010][12];
void dijkstra(){
memset(dis,0x3f,sizeof dis);
priority_queue<ste> q;
q.push({0,s,0});
dis[s][0]=0;
while (q.size()){
auto t=q.top();
q.pop();
if (vis[t.num][t.cnt]) continue;
vis[t.num][t.cnt]=1;
for (auto it:e[t.num]){
if (t.cnt<k&&dis[it.v][t.cnt+1]>dis[t.num][t.cnt]){//如果可以用免费次数
dis[it.v][t.cnt+1]=dis[t.num][t.cnt];
q.push({dis[it.v][t.cnt+1],it.v,t.cnt+1});
}
if (dis[it.v][t.cnt]>dis[t.num][t.cnt]+it.w){//不用免费次数
dis[it.v][t.cnt]=dis[t.num][t.cnt]+it.w;
q.push({dis[it.v][t.cnt],it.v,t.cnt});
}
}
}
}
void insert(int u,int v,int w){
e[u].push_back({v,w});
}
void solve(){
cin>>n>>m>>k>>s>>t;
for (int i=1;i<=m;i++){
int u,v,w;
cin>>u>>v>>w;
insert(u,v,w);
insert(v,u,w);
}
dijkstra();
int ans=1e9;
for (int i=0;i<=k;i++)
ans=min(ans,dis[t][i]);
cout<<ans;
}
Additional：
手玩几个样例可以发现方案数成斐波那契数列，这里的 \(n\) 可以取到 \(10^{18}\) ，数据很大可以利用斐波那契矩阵+快速幂优化
https://oi-wiki.org/math/combinatorics/fibonacci/#矩阵形式
const LL mod=1000000007;
struct matrix{
LL mtx[3][3];
matrix(){memset(mtx,0,sizeof mtx);};
};
matrix operator*(matrix &x,matrix &y){
matrix t;
for (int i=1;i<=2;i++)
for (int j=1;j<=2;j++)
for (int k=1;k<=2;k++)
t.mtx[i][j]=(t.mtx[i][j]+x.mtx[i][k]*y.mtx[k][j])%mod;
return t;
}
matrix qpow(matrix a,LL n){
matrix res;
res.mtx[1][1]=res.mtx[2][2]=1;
while(n){
if (n&1) res=res*a;
a=a*a;
n>>=1;
}
return res;
}
void solve(){
LL n;
cin>>n;
matrix a;
a.mtx[1][1]=a.mtx[1][2]=a.mtx[2][1]=1;
auto ans=qpow(a,n);
cout<<ans.mtx[1][1]<<endl;
}
这是一道经典的博弈论题目，结论是把所有石子异或起来判断是否为 \(0\)
详细证明见：https://oi-wiki.org/math/game-theory/impartial-game/
代码简单就不给出了
浙公网安备 33010602011771号