蓝桥 月赛26 20250405
蓝桥 月赛26 20250403
https://www.lanqiao.cn/oj-contest/senior-26/
A:
题目大意:求 \(\lceil 2025/15\rceil\)
void solve(){
cout<<135;
}
签到
B:
题目大意:

void solve(){
int n,m;
cin>>n>>m;
vector<int> l(n+1),r(n+1);
for (int i=1;i<=n;i++) cin>>l[i]>>r[i];
int p=1;
LL ans=0;
for (int i=1;i<=n;i++){
if (p>=l[i]&&p<=r[i]) continue;
if (abs(l[i]-p)<abs(r[i]-p)){
ans+=abs(l[i]-p);
p=l[i];
}else{
ans+=abs(r[i]-p);
p=r[i];
}
}
cout<<ans;
}
蓝桥特有的神奇题目
因为必须按顺序询问每个区间 \([l,r]\) ,所以枚举记录当前的位置 \(p\)
如果 \(p\) 在下一个区间内,那么不需要移动,如果不在,选择移动到最近的区间端点
C:
题目大意:

void solve(){
int n,k;
cin>>n>>k;
vector<int> a(n+1);
for (int i=1;i<=n;i++) cin>>a[i];
sort(a.begin()+1,a.end());
a[1]+=a[2];
a[2]=0;
sort(a.begin()+1,a.end());
LL ans=0;
for (int i=1;i<=n/2;i++) ans+=a[i];
cout<<ans;
}
可以证明,倒汤圆的操作一定不会使答案变优
假设两碗汤圆为 \(a,b\):
- \(a,b\) 都是在少的 \(\lfloor n/2 \rfloor\) 碗中
- 如果 \(a+b\) 也在少的 \(\lfloor n/2 \rfloor\) 碗中,那么可以得到的总数不变
- 如果 \(a+b\) 不在少的 \(\lfloor n/2 \rfloor\) 碗中,那么可以得到的总数会变为 \(0+k\) 其中 \(k,k<a+b\) 是之前的第 \(\lfloor n/2 \rfloor+1\) 碗
- \(a,b\) 其中一碗在少的 \(\lfloor n/2 \rfloor\) 碗中
- 一碗会变为 \(0\) ,一碗变得更多,那么总数会变少
- \(a,b\) 都不在少的 \(\lfloor n/2 \rfloor\) 碗中
- 一碗会变为 \(0\) ,那么可以得到的总数会减少第 \(\lfloor n/2 \rfloor\) 碗的数量
这里有个题意问题,操作是否必须要做
如果可以不做,那么直接排序输出即可,如果必须要做,那么考虑将操作带来的负收益最小化
第一轮将最小的两碗相互倒,a[1]+=a[2];a[2]=0;
第二轮利用 a[2]=0 ,将 a[3] 中的汤圆移动到 a[2] 中
往后同理,都利用空碗往后倒腾,所以最后的总数为 a[1]+=a[2];a[2]=0; 操作后重新排序的前 n/2 个总和
D:
题目大意:

const int mod=1e9+7;
LL dp[1000010];
void solve(){
dp[1]=1,dp[2]=2;
for (int i=3;i<=1000000;i++)
dp[i]=(dp[i-2]*(i-1)%mod+dp[i-1])%mod;
int t;
cin>>t;
while (t--){
int n;
cin>>n;
cout<<dp[n]<<endl;
}
}
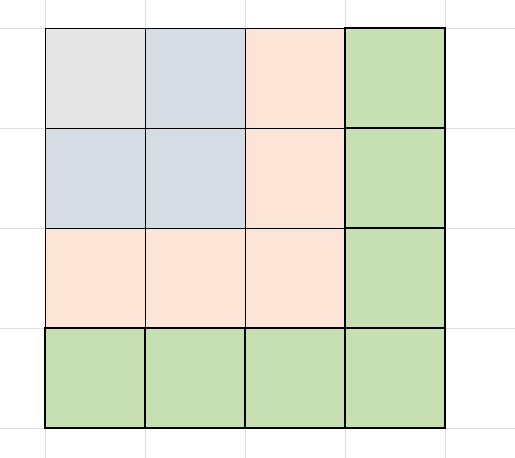
定义 \(dp_i\) 表示防止 \(i\) 个物品的方案数,观察知道 \(dp_1=1,dp_2=2\)
考虑第 \(3\) 个物品的方案数,如因为要保证对称性,所以第 \(3\) 个物品一定可以放在 \((3,3)\) 的位置上,那么这样的方案数为 \(dp_2\)
如果第 \(3\) 个物品放在 \((3,2)\) ,则前 \(2\) 个物品其中一个不能放在 \((1,2),(2,2)\) 上,只能放在 \((2,3)\) 上,则这样的方案数为 \(dp_1\)
同理有放在 \((3,1)\) 的方案数,手玩几次可以得到状态转移方程
其中 \((n-1)*dp_{i-2}\) 代表了第 \(i\) 个物品放在 \(\sum_{j=1}^{i-1}(i,j)\) 的方案数求和,\(dp_{i-1}\) 表示放在 \((i,i)\) 的方案数
E:
题目大意:

void solve(){
int n;
cin>>n;
vector<int> a(n+1);
for (int i=1;i<=n;i++) cin>>a[i];
sort(a.begin()+1,a.end());
for (int i=1;i<=n;i++){
int p=1,ans=0;
while (p<=n){
ans++;
p=lower_bound(a.begin()+1,a.end(),a[p]+i)-a.begin();
}
cout<<ans<<' ';
}
}
首先肯定是读入数据后排序
对每个 \(k\) 都需要扫描一次 \(a\) ,对排序后的 \(a\) 可以做 lower_bound 操作
考虑 \(p\) 记录当前访问到的 \(a_i\) 的位置,每次向后二分找第一个大于等于 \(a_p+k\) 的元素,那么将 \(p\) 移动到找到的元素上
然后计数加一,表示当前可以邀请的朋友数多一
我们的 \(p\) 从 \(1\) 开始,这是最优的,如果从 \(2\) 开始,那么存在 \(a_i\) 导致 \(a_i-a_2<k,a_i-a_1>k\) 这样答案可能会劣
可能会这样想,当 \(p\) 走到了 \(a_i\) 上,如果有 \(a_j-a_2>k,a_j-a_i<k\) 这样不是也会使答案变劣吗?
但其实并不会,因为如果 \(a_j-a_2>k\) 那么一定存在 \(a_j-a_1>1\) ,相当于 \(p\) 不走到 \(a_i\) 上,答案都是一样的
如果走到了 \(a_i\) 上,就有可能存在 \(a_j-a_i>k\) ,会使得答案变优 ,存在变优的可能且一定不会劣,那么就是优的
F:
题目大意:

void solve(){
int n;
cin>>n;
vector<int> a(n+1),b(n+1);
for (int i=1;i<=n;i++) cin>>a[i];
for (int i=1;i<=n;i++) cin>>b[i];
LL sum=0,k=1;
for (int i=2;i<=n;i++){
if (a[i]+min(b[i],b[i-1])>a[i-1]+max(b[i],b[i-1]))
k++;
else
sum+=k*(k-1)/2,k=1;
}
if (k!=1) sum+=k*(k-1)/2;
cout<<sum;
}
首先考虑简单情况,\(r-1=l\) ,即区间只有两个元素
如果当前区间为必胜区间,那么满足
然后区间扩张,如果也为必胜区间,那么满足
两式相加得
考虑区间 \([i-1,i+1]\) ,如果满足
又因为对于 \(b_i,b_j\) , \({\rm{max}}(b_{i},b_{j})-{\rm{min}}(b_i,b_j)>0>{\rm{min}}(b_i,b_j)-{\rm{max}}(b_i,b_j)\)
所以综上可以得出结论,如果区间 \([l,r]\) 是必胜区间,那么他的所有子区间也都为必胜区间
对于每段最大的必胜区间,组合数两个端点有 \(C_{r-l+1}^2=k*(k-1)/2\),累加答案



 浙公网安备 33010602011771号
浙公网安备 33010602011771号