KMP字符串匹配算法

KMP字符串匹配算法

常见的 \(O(n*m)\) 暴力算法

for (int i=1;i<=n;i++){
	int j,k;
	for (j=i,k=1;k<=m;j++,k++){
		if (s1[j]!=s2[k])
			break;
	}
	if (k==m) cout<<i;
}

最外层用 \(i\) 枚举每个字符串首的位置，内层用两个指针 \(j,k\) 分别指向 \(s1,s2\)

如果 s1[j]!=s2[k] ，说明在该位置上不能匹配，则退出内层循环，将 \(i\) 后移

如果内层循环出来后 k==m ，则可以匹配到相同的字符串，输出此时 \(i\) 的位置

这种做法可以简单理解，但是时间复杂度非常的高

---

改进这种做法，发现到每次匹配的过程中我们都会舍弃掉已经匹配过的字符，实际上这些字符可以提供一定的信息

s1:aabaabaabaabaaaa
s2:aabaabaaaa

*图引自董晓算法

模拟一下过程，当 i=1,j=k=9 时不能匹配，暴力做法是将 \(i\) 后移，在下一个字符开始重新遍历

但是可以发现，i=3 时可以直接匹配到 j=k=9 ，这样就节省了 i=2 遍历的时间

---

我们可以打一张表来映射 j,k 的位置与 i 移动的位置的关系

int ne[N];
ne[1]=0;
for (int i=2,j=0;i<=m;i++){
	while (s2[i]!=s2[j+1]&&j) j=ne[j];
	if (s2[i]==s2[j+1]) j++;
	ne[i]=j;
}

双指针对 \(s_2\) 进行操作，用来计算 ne[i] ，即匹配到 i 位置不同后，指针的移动距离

在预处理过程中，\(i\) 指针用来遍历 \(s_2\) 串，\(j\) 指针用来计算最长相同前后缀的长度

如果 \(i,j+1\) 指向的字符不同，那么可以通过之前的结论类似递推的方式计算

while (s2[i]!=s2[j+1]&&j) j=ne[j];//如果j+1指向的元素与i不同，那么考虑从j位置上的最长相同前后缀转移

最终要是都不能匹配，则 \(ne[i]=0\) ，表示不存在最长相同前后缀，应用到匹配过程中，即不能跳跃移动最外层的指针

预处理的时间复杂度为 \(O(m)\)

---

匹配过程中，写法也很类似

for (int i=1,j=0;i<=n;i++){
	while (s1[i]!=s2[j+1]&&j) j=ne[j];
	if (s1[i]==s2[j+1]) j++;
	if (j==m) cout<<i-m+1<<endl;
}

同样是双指针，由于只会遍历 \(s_1\) 中的每个元素最多一次，所以匹配的时间复杂度为 \(O(n)\)

我们这里考虑移动指向 \(s_2\) 的指针 \(j\) 的位置，每次利用 ne 进行回跳

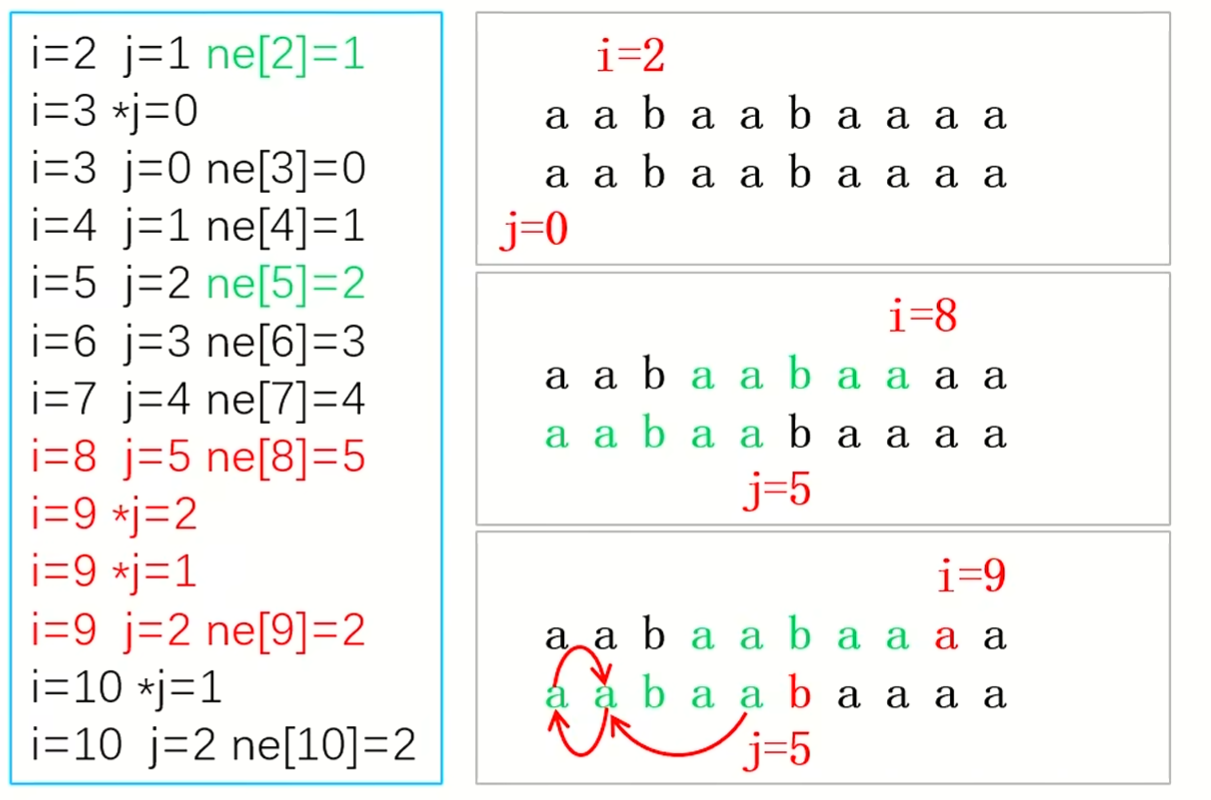
*图引自董晓算法