天梯赛选拔赛 20250321
天梯赛选拔赛 20250321
写在开头:
这场开头率先开出来 \(5\) 道题,本以为一帆风顺,结果没有认真读题导致E题卡了很久(真的很久),看别人排名超过越来越焦虑
A题也可以线段树暴力打 \(60\) 分的,但是已经做昏了头没有写出来板子,甚至纯暴力的 \(25\) 分都没有,理想分数应该在700+,失误很大
B:
题目大意:两个人对给出的一个数轮流进行分割,每次分割为两个正整数,后手选择其中一个继续操作,无法分割的人失败
#include<bits/stdc++.h>
#define cintie ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define Trd int T;cin>>T;while (T--)solve();
#define LLinf 9e18;
#define Iinf 2e9
#define LL long long
#define Lc p<<1
#define Rc p<<1|1
#define lc(x) tr[x].ch[0]
#define rc(x) tr[x].ch[1]
using namespace std;
int main(){
int n;
cin>>n;
for (int i=1;i<=n;i++){
int a;
cin>>a;
if (a%2==1) cout<<"yi wins"<<endl;
else cout<<"jia wins"<<endl;
}
return 0;
}
先说结论,第一次的数为偶数则先手必胜
因为当且仅当遇到的数为 \(1\) 时无法分割,并且奇数只能被分解为一个奇数和偶数,但偶数可以被分解为两个奇数或两个偶数
先手如果遇到偶数 \(n\) 那么只需要分割为 \(1,n-1\) 即可直接获得胜利,如果遇到奇数,后手选择分割后的偶数进行分割,此时后手必胜
G:
题目大意:给定 \(n\) 个元素的序列,可以无限次交换任意两个元素,求出能构造出的最长上升子序列的长度
#include<bits/stdc++.h>
#define cintie ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define Trd int T;cin>>T;while (T--)solve();
#define LLinf 9e18;
#define Iinf 2e9
#define LL long long
#define Lc p<<1
#define Rc p<<1|1
#define lc(x) tr[x].ch[0]
#define rc(x) tr[x].ch[1]
using namespace std;
int a[200010];
int main(){
int n;
cin>>n;
for (int i=1;i<=n;i++)
cin>>a[i];
a[0]=-1e9-1;
sort(a+1,a+n+1);
int ans=0;
for (int i=1;i<=n;i++)
if (a[i]>a[i-1]) ans++;
cout<<ans;
}
签到题
K:
题目大意:给定 \(n,m\) 求出最小的正整数 \(k\) 使得 \(m^k\) 最接近 \(n\)
#include<bits/stdc++.h>
#define cintie ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define Trd int T;cin>>T;while (T--)solve();
#define LLinf 9e18;
#define Iinf 2e9
#define LL long long
#define Lc p<<1
#define Rc p<<1|1
#define lc(x) tr[x].ch[0]
#define rc(x) tr[x].ch[1]
using namespace std;
LL n,m;
void solve(void){
cin>>n>>m;
if (m==1){
cout<<1<<endl;
return;
}
int d=log(n)/log(m);
if (abs(pow(m,d+1)-n)<abs(pow(m,d)-n))
cout<<d+1<<endl;
else
cout<<d<<endl;
}
int main()
{
cintie;
int T;
cin>>T;
while (T--)
solve();
return 0;
}
似曾相识的题目
通过对数计算得到 \(k\) 为小于等于 \(n\) 的 \(m\) 的指数
根据绝对值差决定答案是 \(k,k+1\)
J:
题目大意:有 \(m\) 个人,\(n\times m\) 张牌(\([1,n\times m]\)),现在已知甲手中的 \(n\) 张牌,计算他最少能赢多少轮
#include<bits/stdc++.h>
#define cintie ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define Trd int T;cin>>T;while (T--)solve();
#define LLinf 9e18;
#define Iinf 2e9
#define LL long long
#define Lc p<<1
#define Rc p<<1|1
#define lc(x) tr[x].ch[0]
#define rc(x) tr[x].ch[1]
using namespace std;
bool st[1010];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++) {
int a;
cin>>a;
st[a]=1;
}
int cnt=0;
int ans=0;
for (int i=n*m;i>=1;i--){
if (st[i]) cnt++;
else cnt--;
ans=max(cnt,ans);
}
cout<<ans;
}
从大到小遍历牌面,如果这张牌甲有,他后续可以消耗这张牌赢得一回合,如果这张牌甲没有,那么后面枚举到他有的一张牌,用这张大牌使得甲输一回合
E:
题目大意:有 \(n\) 个区间可以通过,每轮可以左右移动 \(k\) 个单位,求最多第几排不能通过
#include<bits/stdc++.h>
#define cintie ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define Trd int T;cin>>T;while (T--)solve();
#define LLinf 9e18;
#define Iinf 2e9
#define LL long long
#define ULL unsigned long long
#define Lc p<<1
#define Rc p<<1|1
#define lc(x) tr[x].ch[0]
#define rc(x) tr[x].ch[1]
using namespace std;
void solve(){
int n,k;
cin>>n>>k;
int ll=0,rr=1e6;
for (int i=1;i<=n;i++){
int l,r;
cin>>l>>r;
if (rr<l-k||ll>r+k){
cout<<i;
return;
}
ll=max(ll-k,l),rr=min(rr+k,r);
}
cout<<"Phoenix";
}
int main()
{
cintie;
solve();
return 0;
}
理解错了题意,卡了一个多小时,最终还是侥幸在结束前 \(10\) 分钟混出来了 \(95\) 分
考虑即将需要通过的区间 \([l,r]\) ,如果存在能通过的路径,那么当前需要处在区间 \([l-k,r+k]\) 内
然后更新通过后的区间
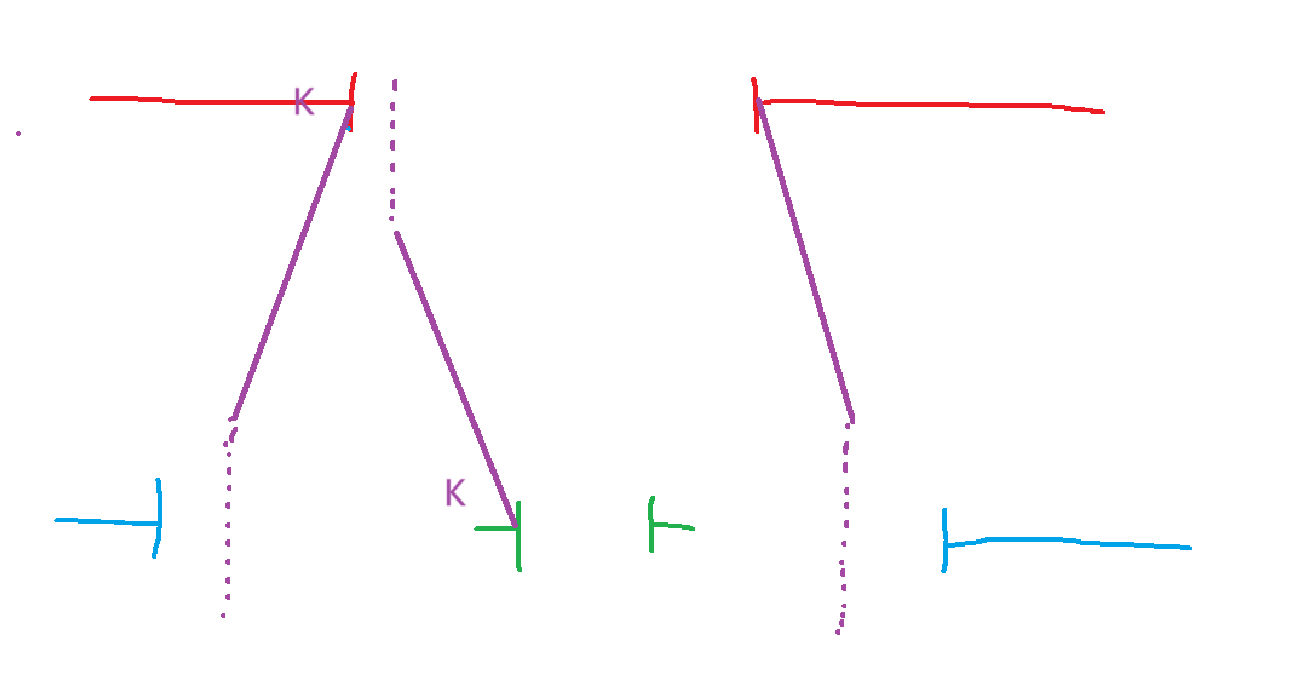
如果上一段区间处在 \(l-k,r+k\) 之外(蓝色),那么可以通过当前区间的所有位置
如果处于 \(l+k,r-k\) 之内(绿色),当前区间有部分不能通过
所以
ll=max(ll-k,l),rr=min(rr+k,r);
I:
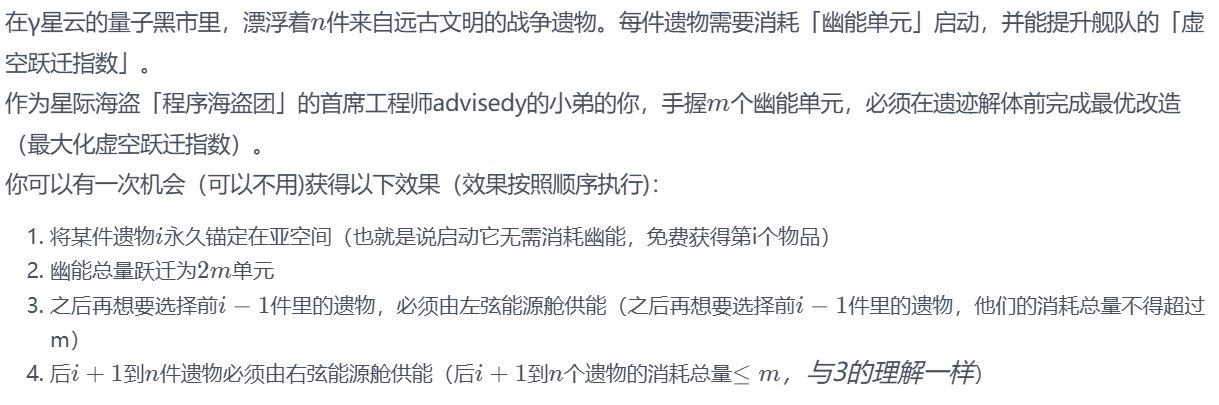
题目大意:
#include<bits/stdc++.h>
#define cintie ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define Trd int T;cin>>T;while (T--)solve();
#define LLinf 9e18;
#define Iinf 2e9
#define LL long long
#define ULL unsigned long long
#define Lc p<<1
#define Rc p<<1|1
#define lc(x) tr[x].ch[0]
#define rc(x) tr[x].ch[1]
using namespace std;
int n,m;
int w[1010],v[1010];
int dp1[1010][1010];
int dp2[1010][1010];
void solve(){
cin>>n>>m;
for (int i=1;i<=n;i++)
cin>>w[i]>>v[i];
for (int i=1;i<=n;i++){
for (int j=0;j<=m;j++){
dp1[i][j]=dp1[i-1][j];
if (j>=w[i]) dp1[i][j]=max(dp1[i][j],dp1[i-1][j-w[i]]+v[i]);
}
}
for (int i=1;i<=n;i++){
for (int j=0;j<=m;j++){
dp2[i][j]=dp2[i-1][j];
if (j>=w[n-i+1]) dp2[i][j]=max(dp2[i][j],dp2[i-1][j-w[n-i+1]]+v[n-i+1]);
}
}
int ans=0;
for (int i=1;i<=n;i++)
ans=max(ans,dp1[i-1][m]+dp2[n-i][m]+v[i]);
cout<<ans;
}
int main()
{
cintie;
solve();
return 0;
}
题目太长当时没想认真看下去,结果是一道简单的DP
写两轮DP,分别记录前 \(i\) 个物品装 \(j\) 容量背包的最大价值和后 \(i\) 个物品装 \(j\) 容量背包的最大价值
最后枚举免费获得的物品,分别计算前 \([1,i-1]\) 和 \([i+1,n]\) 物品装 \(m\) 背包的最大值即可
D:
题目大意:

#include<bits/stdc++.h>
#define cintie ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define Trd int T;cin>>T;while (T--)solve();
#define LLinf 9e18;
#define Iinf 2e9
#define LL long long
#define Lc p<<1
#define Rc p<<1|1
#define lc(x) tr[x].ch[0]
#define rc(x) tr[x].ch[1]
using namespace std;
struct node{
int now,stp,cnt;
};
int n,k,a,b,x,y;
int dis[200010];
void bfs(int s){
queue<node> q;
memset(dis,0x3f,sizeof dis);
q.push({s,0,0});
dis[s]=0;
while (q.size()){
auto t=q.front();
q.pop();
if (dis[(t.now+x)%n]>t.stp+1){
dis[(t.now+x)%n]=t.stp+1;
q.push({(t.now+x)%n,t.stp+1,t.cnt});
}
if (dis[(t.now-y+n)%n]>t.stp+1){
dis[(t.now-y+n)%n]=t.stp+1;
q.push({(t.now-y+n)%n,t.stp+1,t.cnt});
}
if (dis[(t.now+n/2)%n]>t.stp+1 && t.cnt<k){
dis[(t.now+n/2)%n]=t.stp+1;
q.push({(t.now+n/2)%n,t.stp+1,t.cnt+1});
}
}
}
int main()
{
cin>>n>>k>>a>>b>>x>>y;
if (a==b){
cout<<0;
return 0;
}
bfs(a);
if (dis[b]==0x3f3f3f3f) cout<<-1;
else cout<<dis[b];
return 0;
}
差点被骗,其实是简单的BFS题目,每个点根据步数的顺序最多只能被标记一次,时间复杂度为 \(O(n)\)
struct node{
int now,stp,cnt;
};
队列元素需要记录当前点的位置 now,当前的步数 stp,以及所用的量子纠缠数 cnt
H:
题目大意:给定一个序列,两人轮流从两端选择一个数,在最佳策略下求两者博弈后能获得的最大得分
#include<bits/stdc++.h>
#define cintie ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define Trd int T;cin>>T;while (T--)solve();
#define LLinf 9e18;
#define Iinf 2e9
#define LL long long
#define ULL unsigned long long
#define Lc p<<1
#define Rc p<<1|1
#define lc(x) tr[x].ch[0]
#define rc(x) tr[x].ch[1]
using namespace std;
int n;
int a[1010];
int dp[1010][1010];
int sum;
void solve(){
cin>>n;
for (int i=1;i<=n;i++){
cin>>a[i];
dp[i][i]=a[i];
sum+=a[i];
}
for (int len=2;len<=n;len++){
for (int i=1;i+len-1<=n;i++){
dp[i][i+len-1]=max(a[i]-dp[i+1][i+len-1],a[i+len-1]-dp[i][i+len-2]);
}
}
cout<<(sum+dp[1][n])/2<<' '<<(sum-dp[1][n])/2;
}
int main()
{
cintie;
solve();
return 0;
}
这是真不会了,依然是DP动态规划
\(dp_{i,j}\) 表示在元素 \(a_i,a_j\) 之间选择,先手比后手多的分数
状态转移方程为
如果当前取走 \(a_i\) 那么后手会选择在区间 \([i+1,j]\) 之间的最优解 \(dp_{i+1,j}\) ,同理有取走 \(a_j\) 的方案
先手玩家会选择对自己最有利的一项,即使得自己的分数与后手的分数差值最大



 浙公网安备 33010602011771号
浙公网安备 33010602011771号