线性DP应用及滚动数组优化

线性DP应用及滚动数组优化

---

题目描述

设 \(A\) 和 \(B\) 是两个字符串。我们要用最少的字符操作次数，将字符串 \(A\) 转换为字符串 \(B\)。这里所说的字符操作共有三种：

1. 删除一个字符；
2. 插入一个字符；
3. 将一个字符改为另一个字符。

\(A, B\) 均只包含小写字母。

---

典型的动态规划问题，用空间存储已经计算的状态，再来递推未知的状态

• 记状态变量 \(dp_{i,j}\) 表示 \([A_1,A_i]\) 到 \([B_1,B_j]\) 的编辑距离

• 处理边界情况 \(dp_{i,0}=i,dp_{0,j}=j\) 这表示将一个非空串修改到空串的操作数

• 状态转移方程

对于枚举 \(A_i,B_j\) 存在两种情况：\(A_i=B_j\ {\rm{or}}\ A_i\ne B_j\)

第一种情况时，\(A_i\) 已经与 \(B_j\) 配对成功，那么不需要进行操作，所以 \(dp_{i,j}=dp_{i-1,j-1}\) 转移得来

第二种情况，可以执行三种操作

1. 删除一个字符即删去 \(A_i\)，\(dp_{i,j}=dp_{i-1,j}+1\)
2. 插入一个字符即在 \(A_i\) 后插入 \(B_j\) ，\(dp_{i,j}=dp_{i,j-1}+1\)
3. 将一个字符改为另一个字符即把 \(A_i\) 改为 \(B_i\) ，\(dp_{i,j}=dp_{i-1,j-1}+1\)

*删去 \(A_i\) 与 在 \(A_i\) 后插入 \(B_j\) 同样的和对操作 \(B\) 等价

综上可以得出状态转移方程

\[dp_{i,j}=\begin{cases} dp_{i-1,j-1} & \text{$A_i=B_j$}\\\\ {\rm{min}}(dp_{i-1,j},dp_{i,j-1},dp_{i-1,j-1})+1 & \text{$A_i\ne B_j$} \end{cases} \]

string a,b;
cin>>a>>b;
a='#'+a;
b='#'+b;//优化下标从1开始
for (int i=1;i<a.size();i++) dp[i][0]=i;
for (int j=1;j<b.size();j++) dp[0][j]=j;//边界值初始化
for(int i=1;i<a.size();i++){
	for (int j=1;j<b.size();j++){
		if (a[i]==b[j]) dp[i][j]=dp[i-1][j-1];
		else dp[i][j]=min(dp[i-1][j],min(dp[i-1][j-1],dp[i][j-1]))+1;
	}
}	
cout<<dp[a.size()-1][b.size()-1];

这样的时间复杂度与空间复杂度都为 \(O(nm)\) ，事实上可以对空间进行再次优化

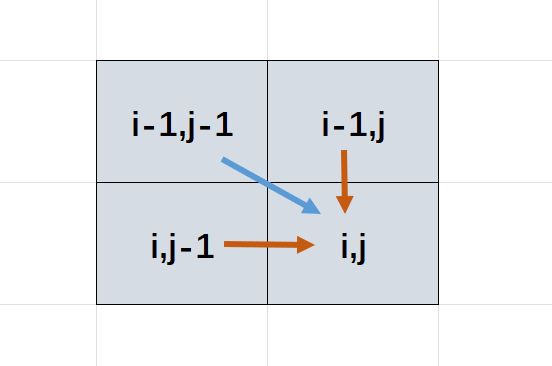
上图可以看出，\(dp_{i,j}\) 的状态只会与 \(dp_{i-1,j-1},dp_{i-1,j},dp_{i,j-1}\) 有关

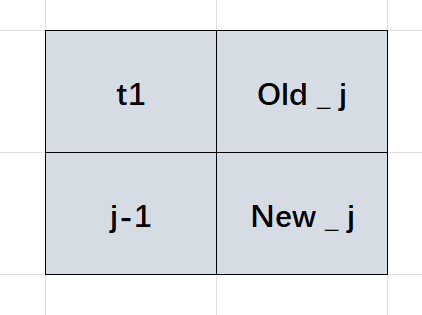
可以设置临时变量来记录 \(dp_{i-1,j-1}\) ，重复空间来从旧的 \(dp_j\) 递推到新的 \(dp_j\)

例如

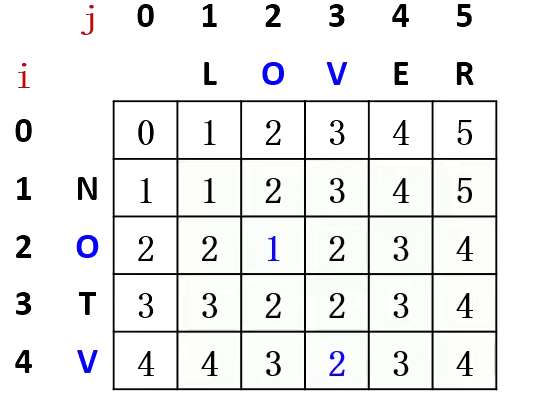
*引自董晓算法

for (int i=1;i<b.size();i++) dp[i]=i;//初始化边界
for(int i=1;i<a.size();i++){
	int t1=dp[0]++;//从最左侧开始赋值t1
	for (int j=1;j<b.size();j++){
		int t2=dp[j];//t2记录旧空间内的dp_j
		if (a[i]==b[j]) dp[j]=t1;
		else dp[j]=min(t1,min(dp[j-1],dp[j]))+1;//更新新递推出的dp_j
		t1=t2;//将t1移动到旧空间内的dp_j上，进行下一次操作
	}
}	
cout<<dp[b.size()-1];