集训3 20250127
集训3 20250127
牛客竞赛_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ
A:
题目大意:给定 \(n\) ,两个人轮流可以使 \(n\) 减去一个任意小于它且与它互质的数,求最后甲能否取胜
#include<bits/stdc++.h>
using namespace std;
int main()
{
long long n;
cin>>n;
if (n%2==0) cout<<"NO";
else cout<<"YES";
return 0;
}
与偶数互质的数一定为奇数,那么每个人的最优策略就是只减去 \(1\)
如果某人的 \(n\) 现在为偶数,那么一定会失败
M:
题目大意:给定 \(8\) 个字符,判断是否符合条件
#include<bits/stdc++.h>
using namespace std;
int main()
{
map<char,int> a;
char s;
for (int i=0;i<8;i++){
cin>>s;
a[s]++;
}
if (a['c']!=1||a['d']!=1||a['e']!=1||a['n']!=1||a['o']!=2||a['r']!=1||a['w']!=1)
cout<<"I AK IOI";
else cout<<"happy new year";
return 0;
}
签到,但是送了一发
F:
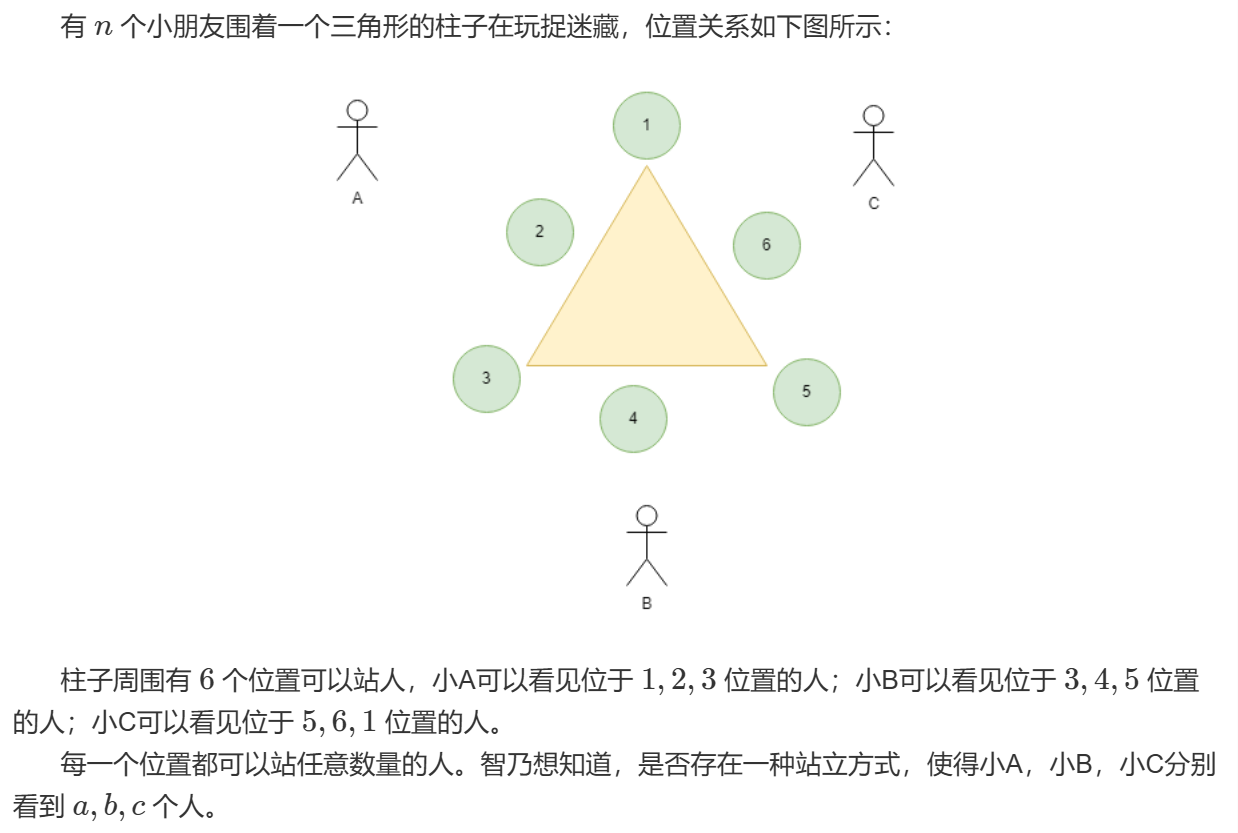
题目大意:
#include<bits/stdc++.h>
using namespace std;
void solve(void){
int n,a,b,c;
cin>>n>>a>>b>>c;
if (a+b+c<n||a+b+c>2*n){
cout<<"NO"<<endl;
return;
}
cout<<"YES"<<endl;
return;
}
int main()
{
int T;
cin>>T;
while (T--)
solve();
return 0;
}
题目可以转化为不等式:
\[\begin{cases}
x_1+x_2+x_3=A\\
x_3+x_4+x_5=B\\
x_5+x_6+x_1=C
\end{cases}
\]
等式两侧分别求和有:
\[2*(x_1+x_3+x_5)+x_2+x_4+x_6=A+B+C
\]
设球总共有 \(N\) 个,那么 $\sum_{i=1}^6 x_i=N\ $
\[\implies N\le A+B+C\le2N
\]
所以,当且仅当上述不等式成立时,存在答案
L:
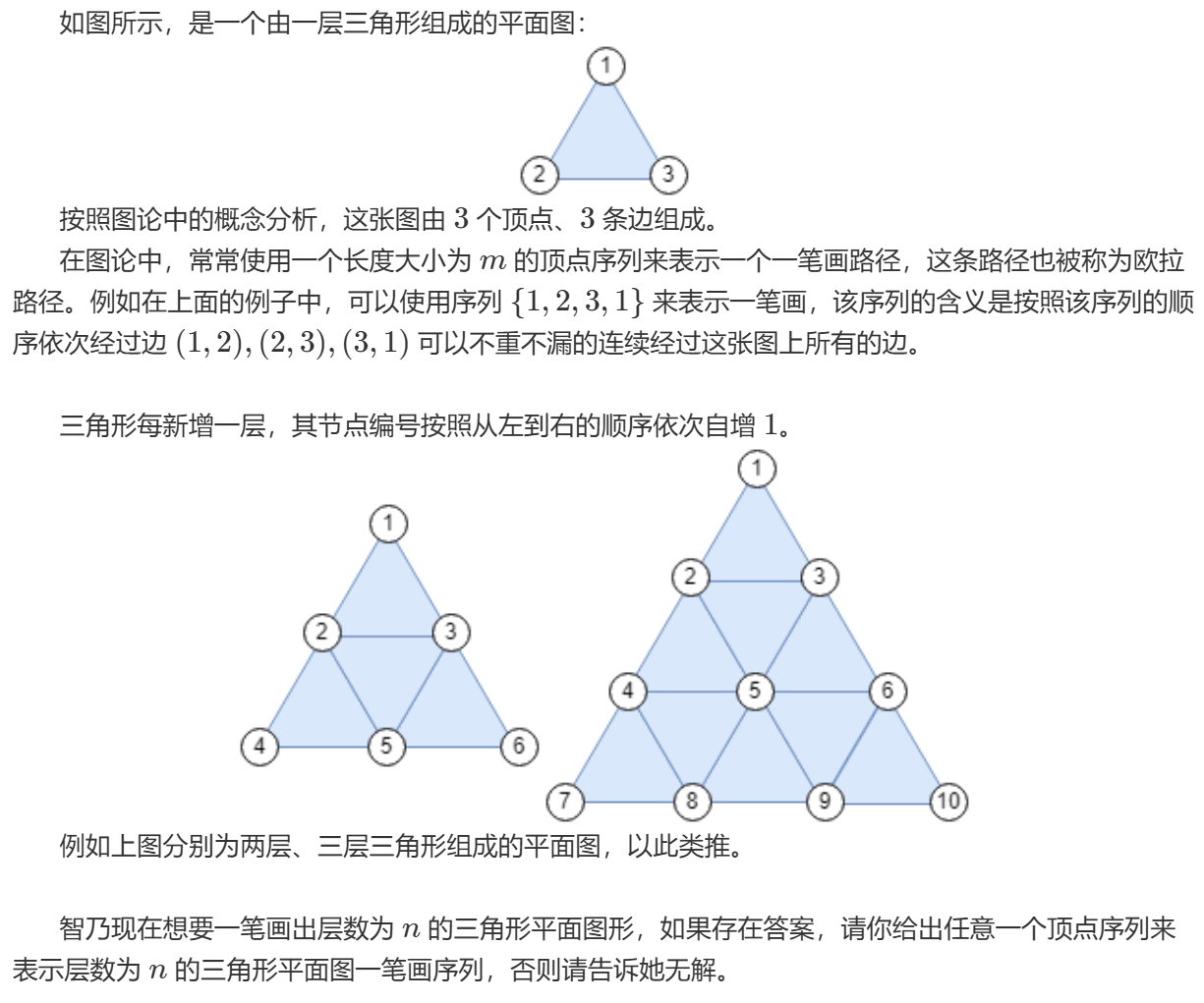
题目大意:
#include<bits/stdc++.h>
using namespace std;
string s[9]={
"0",
"1",
"2 3 1 2",
"4 5 6 3 5 2 3 1 2 4",
"7 8 9 10 6 9 5 8 4 5 6 3 5 2 3 1 2 4 7",
"11 12 13 14 15 10 14 9 13 8 12 7 8 9 10 6 9 5 8 4 5 6 3 5 2 3 1 2 4 7 11",
"16 17 18 19 20 21 15 20 14 19 13 18 12 17 11 12 13 14 15 10 14 9 13 8 12 7 8 9 10 6 9 5 8 4 5 6 3 5 2 3 1 2 4 7 11 16",
"22 23 24 25 26 27 28 21 27 20 26 19 25 18 24 17 23 16 17 18 19 20 21 15 20 14 19 13 18 12 17 11 12 13 14 15 10 14 9 13 8 12 7 8 9 10 6 9 5 8 4 5 6 3 5 2 3 1 2 4 7 11 16 22",
"29 30 31 32 33 34 35 36 28 35 27 34 26 33 25 32 24 31 23 30 22 23 24 25 26 27 28 21 27 20 26 19 25 18 24 17 23 16 17 18 19 20 21 15 20 14 19 13 18 12 17 11 12 13 14 15 10 14 9 13 8 12 7 8 9 10 6 9 5 8 4 5 6 3 5 2 3 1 2 4 7 11 16 22 29"
};
int main()
{
int n;
cin>>n;
cout<<"YES"<<endl;
cout<<s[n+1];
return 0;
}
直接打表算了
DFS判断欧拉回路:
#include<bits/stdc++.h>
using namespace std;
struct edge{
int v,id;
};
int b[10010];
vector<edge> e[10010];
int idx;
bool vis[10010];
vector<int> ans;
void insert(int u,int v){
e[u].push_back({v,idx});
e[v].push_back({u,idx});
idx++;//记录点
}
void dfs(int x){
for (auto [v,id]:e[x]){
if (vis[id]) continue;//判断是否经过
vis[id]=1;
dfs(v);
}
ans.push_back(x);//回溯加入答案
}
int main()
{
int n;
cin>>n;
b[0]=1;
for (int i=1;i<=n;i++)
b[i]=b[i-1]+i;//计算最左侧端点值
for (int i=0;i<n;i++){
for (int j=0;j<=i;j++){//插入边
insert(b[i]+j,b[i+1]+j);
insert(b[i+1]+j,b[i+1]+j+1);
insert(b[i+1]+j+1,b[i]+j);
}
}
dfs(1);
cout<<"YES"<<endl;;
for (auto iter:ans) cout<<iter<<' ';
return 0;
}
C:
题目大意:给定 \(n\) 个单词,在可以使用删除键的情况下,求解输出这 \(n\) 个单词最少的敲键盘数
#include<bits/stdc++.h>
using namespace std;
int n,m,l,r;
string s[1000010];
int tr[1000010][30];
int idx,cnt[1000010],mem[1000010],memcnt;
int getnum(char c){
return c-'a';
}
void insert(string s){
int p=0,len=s.size();
for (int i=0;i<len;i++){
int c=getnum(s[i]);
if (!tr[p][c]){
tr[p][c]=++idx;
mem[memcnt]++;
}
p=tr[p][c];
}
}
bool cmp(string x,string y){
return x.size()>y.size();
}
int main()
{
cin>>n>>m;
for (int i=0;i<n;i++){
cin>>s[i];
}
sort(s,s+n,cmp);
for(int i=0;i<n;i++){
insert(s[i]);
memcnt++;
}
cin>>l>>r;
sort(mem,mem+memcnt);
long long ans=idx;
for (int i=0;i<memcnt-1;i++)
ans+=1ll*mem[i];
cout<<ans;
return 0;
}
采用字典树模拟,公共前缀不用重复输出
实际上可以解决地更容易,原题可以转化为求解不等式的极小值:
\[ans=S_0+\sum_{i=1}^{N-1}S_i+S_{i-1}-2*lcp(S_i,S_{i-1})
\\ \implies ans=2*(\sum_{i=0}^{N-1}S_i-\sum_{i=1}^{N-1}lcp(S_i,S_{i-1}))-S_{N-1}
\]
贪心计算
\[max(\sum_{i=1}^{N-1}lcp{S_i,S_{i-1}})\quad and\quad max(S_{N-1})
\]
答案即为 2 * (字符串组全部字符和 - 相邻字符串公共最长前缀长度) - 最长字符串长度
#include<bits/stdc++.h>
using namespace std;
int n,m;
int x,y,z;
string s[100010];
int lcp(string a,string b){//计算相邻公共最长前缀的长度
int i=0;
while(i<a.size()&&i<b.size()&&a[i]==b[i]) ++i;
return i;
}
int main()
{
cin>>n>>m;
for (int i=1;i<=n;i++) cin>>s[i];
sort(s+1,s+n+1);
for (int i=1;i<=n;i++){
x+=2*(int)s[i].size();
if (i!=1) y+=2*lcp(s[i],s[i-1]);
z=max(z,(int)s[i].size());
}
cout<<x-y-z;
return 0;
}
E:
题目大意:

#include<bits/stdc++.h>
using namespace std;
const int INF=1e9+7;
int n,k;
vector<int> a,b;
bool judge(int x){//x看作时间的两倍,避免浮点运算
int p1=0,p2=0;//双指针
long long res=0;
for (auto iter:a){
while(p2<b.size()&&b[p2]<iter) p2++;//记录iter小球前一个碰到的球
while(p1<b.size()&&b[p1]<=iter+x) p1++;//记录iter小球最远能碰到哪个小球
res+=p1-p2;//记录这个区间内所有能碰到的小球的个数
}
return res<k;//二分判断
}
int main()
{
cin>>n>>k;
for (int i=1;i<=n;i++){
int x,y;
cin>>x>>y;
if (y==1)
a.push_back(x);//记录向右小球
else
b.push_back(x);//记录向左小球
}
sort(a.begin(),a.end());//按照坐标排序
sort(b.begin(),b.end());
int l=0,r=INF;
while(l+1!=r){
int mid=l+r>>1;
if (judge(mid))
l=mid;
else
r=mid;
}
if (r==INF){
cout<<"NO\n";
return 0;
}else{
cout<<"YES"<<endl;
printf("%.6lf",(double)r/2);
return 0;
}
}
二分时间,利用双指针优化计算碰撞次数
G:
题目大意:计算 \(\sum_{i=1}^n n\ \%\ i\) 排序后前 \(k\) 项和
#include<bits/stdc++.h>
using namespace std;
int main()
{
long long n,k;
cin>>n>>k;
long long l=0,r=n+1;
long long sum,val;
while (l+1!=r){
long long mid=l+r>>1;
long long cnt=0;
for (long long ll=1,rr;ll<=n;ll=rr+1){
rr=n/(n/ll);
long long t=n-n/ll*ll,kk=n/ll;
if (t<mid) continue;
cnt+=min((t-mid)/kk+1,rr-ll+1);
}
if (cnt>=k) l=mid;
else {
sum=cnt;
val=mid;
r=mid;
}
}
long long ans=1ll*(k-sum)*(val-1);
for (long long ll=1,rr;ll<=n;ll=rr+1){
rr=n/(n/ll);
long long t=n-n/ll*ll,kk=n/ll;
if (t<val) continue;
long long len=min((t-val)/kk+1,rr-ll+1);
ans+=1ll*(t*2-kk*(len-1))*len/2;
}
cout<<ans;
return 0;
}
利用二分查找第 \(k\) 大的数是多少
\[x\ \%\ y=x-\lfloor \frac{y}{x}\rfloor\cdot x
\]
long long l=0,r=n+1;//左右边界
long long sum,val;
while (l+1!=r){
long long mid=l+r>>1;
long long cnt=0;//cnt记录当前大于mid的数有多少
for (long long ll=1,rr;ll<=n;ll=rr+1){//分块计算
rr=n/(n/ll);//计算右边界
long long t=n-n/ll*ll,kk=n/ll;//t计算当前的n%i(分块的第一个元素),kk记录商(公差)
if (t<mid) continue;//如果t比mid还要小,那么就跳过这个分块
cnt+=min((t-mid)/kk+1,rr-ll+1);//累加cnt,在没有超出边界的情况下加上区间内大于mid的元素的数量
//(t-mid)/kk+1,根据公差计算元素个数
}
if (cnt>=k) l=mid;//如果数量超过了二分的mid,说明mid取小了,满足的元素个数多于k
else {//mid取大了,那就需要记录cnt和mid的值,更新右边界
sum=cnt;
val=mid;
r=mid;
}
}
只在更新 r 的时候记录 sum 和 val 的原因是更新 r 时的 mid 已经满足条件了
例如 n=10,k=5 时,排序后的商为 4 3 2 2 1 1 0 0 0 0 ,第五个数和第六个数的值相同,为了便于计算就记录不同于第 k 个数前的位置,cnt=4
long long ans=1ll*(k-sum)*(val-1);计算第k个数有多个元素的值相同情况
for (long long ll=1,rr;ll<=n;ll=rr+1){
rr=n/(n/ll);
long long t=n-n/ll*ll,kk=n/ll;
if (t<val) continue;//如果t比val还要小,那么就跳过这个分块
long long len=min((t-val)/kk+1,rr-ll+1);//计算分块长度
ans+=1ll*(t*2-kk*(len-1))*len/2;//等差数列累加答案
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号