快速幂优化高精度乘法

NOI 1.6 12

题目描述

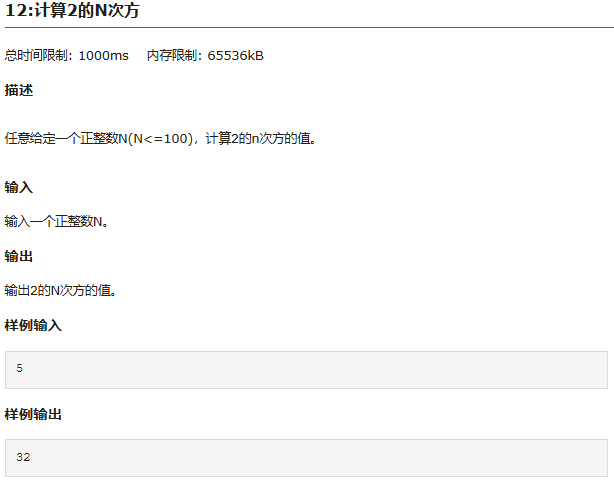
题目给出的 \(n\) 最大可以取到 \(100\) ，即计算 \(2^{100}\) ，明显是超过 long long 的 \(2^{63}-1\)，所以需要使用高精度来计算幂次方的乘法

• 简单的高精度，即每次计算一个小整数乘上一个大整数

循环 \(n\) 次，每次对上一次的积都乘以 \(2\)

vector<int> ans = { 1 };//注意，需要对ans的第一位进行赋初值为1
for (int i = 1; i <= n; i++)
	ans = highdouble(ans);

然后就是简单高精度乘法的模板

vector<int> highdouble(vector<int> x) {
	vector<int> res;//定义返回数组
	int t = 0;//进位变量
	for (int i = 0; i < x.size(); i++) {
		t += 2 * x[i];//计算乘2的积
		res.push_back(t % 10);//取尾数放入
		t /= 10;
	}
	while (t) {//如果进位t还有值，就继续放入
		res.push_back(t % 10);
		t /= 10;
	}
	return res;//返回答案
}

以上的代码仅只用于大整数乘一个小整数，不能完成对两个大整数求积的操作、

简单的高精度计算的时间复杂度大约在 \(O(n^2)\) ，我们也可以使用快速幂的办法将时间复杂度优化到更低

• 快速幂高精度计算

vector<int> quickpower(int b) {//快速幂函数
    vector<int> res, a;//使用vector来存储数据
    res.push_back(1);//对res第一项继续预处理
    a.push_back(2);//放入底数2
    while (b)//快速幂模板
    {
        if (b & 1) res = highplus(res, a);//使用高精度乘法计算
        a = highplus(a, a);//高精度倍增计算因子
        b >>= 1;
    }
    return res;
}

这里的高精度乘法需要计算两个大整数的积，采用错位相乘法

vector<int> highplus(vector<int>& x, vector<int>& y) {
    vector<int> temp(x.size() + y.size() + 1, 0);
    for (int i = 0; i < x.size(); i++)
        for (int j = 0; j < y.size(); j++)
            temp[i + j] += x[i] * y[j];
    int t = 0;
    for (int i = 0; i < temp.size(); i++) {
        t += temp[i];
        temp[i] = t % 10;
        t /= 10;
    }
    while (t > 0) {
        temp.push_back(t % 10);
        t /= 10;
    }
    while (temp.size() > 1 && temp.back() == 0) temp.pop_back();
    return temp;
}

其中，将 temp 赋值一个最大长度，即两个因子的长度和加 \(1\) ，并赋初值都为 \(0\)

循环两层计算相应位置上的乘积 temp[i + j] += x[i] * y[j] （原理这里不做赘述）

最后处理进位的问题，遍历整个 temp 数组，对每一位都继续进位操作

 t += temp[i];
 temp[i] = t % 10;
 t /= 10;
 
 while (t > 0) {//如果进位t还有值，就继续放入
    temp.push_back(t % 10);
    t /= 10;
 }

对 temp 数组去除前导 \(0\) 后返回高精度乘法的结果

---

经过实测，朴素的高精度乘法在规定的 \(1s\) 内最多只能计算到 \(2^{11438}\)，而采用快速幂则可以计算到 \(2^{2^{15-1}}=2^{32767}\)

是一种极大的优化方案，如果我们的底数更大的话，快速幂的优势会变得更大

完整AC代码：

朴素算法

#include <vector>
#include <iostream>
using namespace std;

int n;
vector<int> ans = { 1 };

vector<int> highdouble(vector<int> x) {
	vector<int> res;
	int t = 0;
	for (int i = 0; i < x.size(); i++) {
		t += 2 * x[i];
		res.push_back(t % 10);
		t /= 10;
	}
	while (t) {
		res.push_back(t % 10);
		t /= 10;
	}
	return res;
}

int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
		ans = highdouble(ans);
	for (int i = ans.size() - 1; i >= 0; i--) cout << ans[i];
	return 0;
}

快速幂

#include <vector>
#include <iostream>
using namespace std;

int n;

vector<int> highplus(vector<int>& x, vector<int>& y) {
	vector<int> temp(x.size() + y.size() + 1, 0);
	for (int i = 0; i < x.size(); i++)
		for (int j = 0; j < y.size(); j++)
			temp[i + j] += x[i] * y[j];
	int t = 0;
	for (int i = 0; i < temp.size(); i++) {
		t += temp[i];
		temp[i] = t%10;
		t /= 10;
	}
	while (t > 0) {
		temp.push_back(t % 10);
		t /= 10;
	}
	while (temp.size() > 1 && temp.back() == 0) temp.pop_back();
	return temp;
}

vector<int> quickpower(int b) {
	vector<int> res, a;
	res.push_back(1);
	a.push_back(2);
	while (b)
	{
		if (b & 1) res = highplus(res, a);
		a = highplus(a, a);
		b >>= 1;
	}
	return res;
}

int main()
{
	cin >> n;
	auto ans = quickpower(n);
	for (int i = ans.size() - 1; i >= 0; i--) cout << ans[i];
	return 0;
}