UVa OJ 113 - Power of Cryptography (密文的乘方)

Time limit: 3.000 seconds
限时: 3.000秒

 

Background
背景

Current work in cryptography involves (among other things) large prime numbers and computing powers of numbers modulo functions of these primes. Work in this area has resulted in the practical use of results from number theory and other branches of mathematics once considered to be of only theoretical interest.

This problem involves the efficient computation of integer roots of numbers.

 

The Problem
问题

Given an integer n ≥ 1 and an integer p ≥ 1 you are to write a program that determines 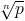, the positive n^th root of p. In this problem, given such integers n and p, p will always be of the form kⁿ for an integer k (this integer is what your program must find).

 

The Input
输入

The input consists of a sequence of integer pairs n and p with each integer on a line by itself. For all such pairs 1 ≤ n ≤ 200, 1 ≤ p ≤ 10¹⁰¹and there exists an integer k, 1 ≤ k ≤ 10⁹ such that kⁿ = p.

The Output
输出

For each integer pair n and p the value 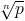should be printed, i.e., the number k such that kⁿ = p.

 

Sample Input

2
16
3
27
7
4357186184021382204544

 

Sample Output

4
3
1234

 

Analysis

这道题刚一拿到手着实让我吓了一跳，难道是让我来实现大数的数值算法吗？我一开始想到了大整数运算，后来想到牛顿迭代法。最后发现给定的p值并没有超过double能表示的范围，汗……啥也不说了，看代码吧。

 

Solution

#include <iostream>
#include <math.h>
using namespace std;
int main(void) {
	for (double dNum, dPow; cin >> dPow >> dNum;
		cout << (int)(pow(dNum, 1.0 / dPow) + 0.5) << endl);
	return 0;
}