新征程5.4 动态规划(一)
动态规划
\(by\) Cr_deviance
DP入门
B3635 B3637
这是两道DP的入门题,可以先从这两题入手,熟悉一下动态规划的基本思想,以及动态规划中状态及状态转移方程的设计思路,帮助各位初学者(julao)对动态规划有一个初步的了解。不讲,逃(
记忆化搜索
记忆化搜索(Memoization Search):是一种通过存储已经遍历过的状态信息,从而避免对同一状态重复遍历的搜索算法。
记忆化搜索是动态规划的一种实现方式。在记忆化搜索中,当算法需要计算某个子问题的结果时,它首先检查是否已经计算过该问题。如果已经计算过,则直接返回已经存储的结果;否则,计算该问题,并将结果存储下来以备将来使用。
举个例子,比如「斐波那契数列」的定义是:\(f(0) = 0, f(1) = 1, f(n) = f(n - 1) + f(n - 2)\)。如果我们使用递归算法求解第 \(n\) 个斐波那契数,则对应的递推过程如下: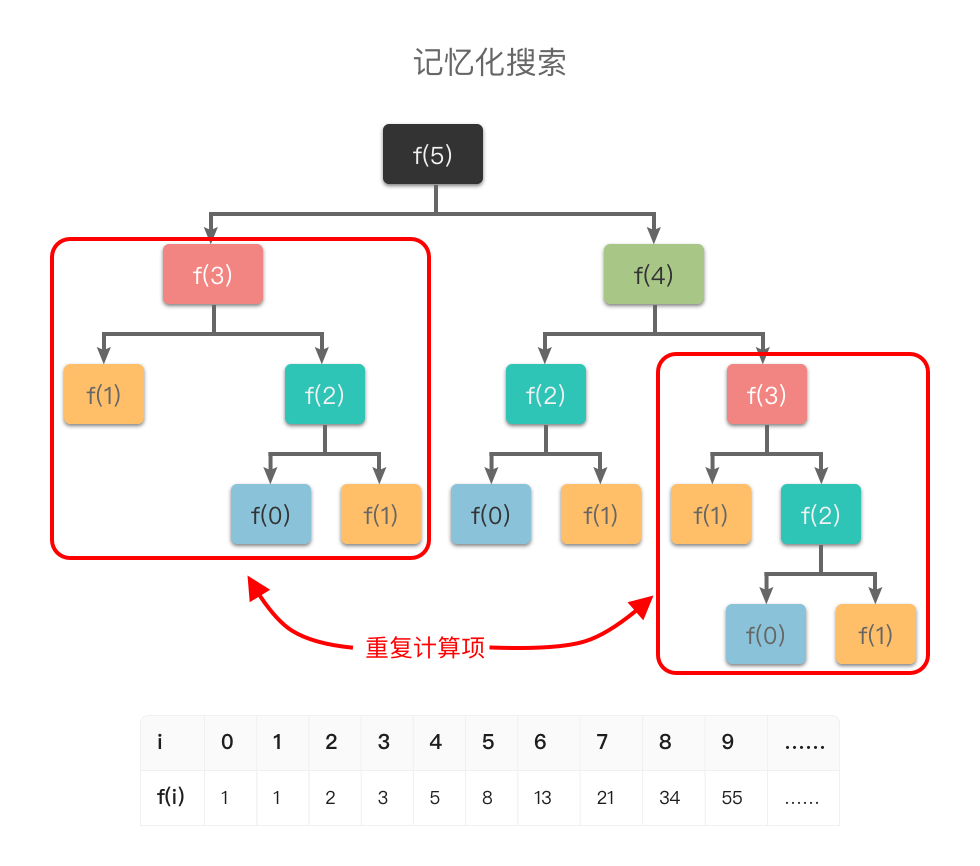
从图中可以看出:如果使用普通递归算法,想要计算 \(f(5)\),需要先计算 \(f(3)\) 和 \(f(4)\),而在计算 \(f(4)\) 时还需要计算 \(f(3)\)。这样 \(f(3)\) 就进行了多次计算,同理 \(f(0)\)、\(f(1)\)、\(f(2)\) 都进行了多次计算,从而导致了重复计算问题。
为了避免重复计算,在递归的同时,我们可以使用一个缓存(数组或哈希表)来保存已经求解过的 \(f(k)\) 的结果。如上图所示,当递归调用用到 \(f(k)\) 时,先查看一下之前是否已经计算过结果,如果已经计算过,则直接从缓存中取值返回,而不用再递推下去,这样就避免了重复计算问题。
使用「记忆化搜索」方法解决斐波那契数列的代码如下:
class Solution:
def fib(self, n: int) -> int:
# 使用数组保存已经求解过的 f(k) 的结果
memo = [0 for _ in range(n + 1)]
return self.my_fib(n, memo)
def my_fib(self, n: int, memo: List[int]) -> int:
if n == 0:
return 0
if n == 1:
return 1
# 已经计算过结果
if memo[n] != 0:
return memo[n]
# 没有计算过结果
memo[n] = self.my_fib(n - 1, memo) + self.my_fib(n - 2, memo)
return memo[n]
我们在使用记忆化搜索解决问题的时候,其基本步骤如下:
写出问题的动态规划「状态」和「状态转移方程」。
定义一个缓存(数组或哈希表),用于保存子问题的解。
定义一个递归函数,用于解决问题。在递归函数中,首先检查缓存中是否已经存在需要计算的结果,如果存在则直接返回结果,否则进行计算,并将结果存储到缓存中,再返回结果。
在主函数中,调用递归函数并返回结果
P1352 没有上司的舞会
P1434 [SHOI2002] 滑雪
两个比较典的例题。
背包DP
背包问题的定义
一个可承载重量为 \(W\) 的背包和 \(N\) 件物品,每件物品有一个重量 \(w\) 和一个价值 \(v\)。现在让你用这个背包装物品,要求装入的物品总重量不能超过背包可承载重量 \(W\),同时使装入物品的总价值最大。
背包问题的分类
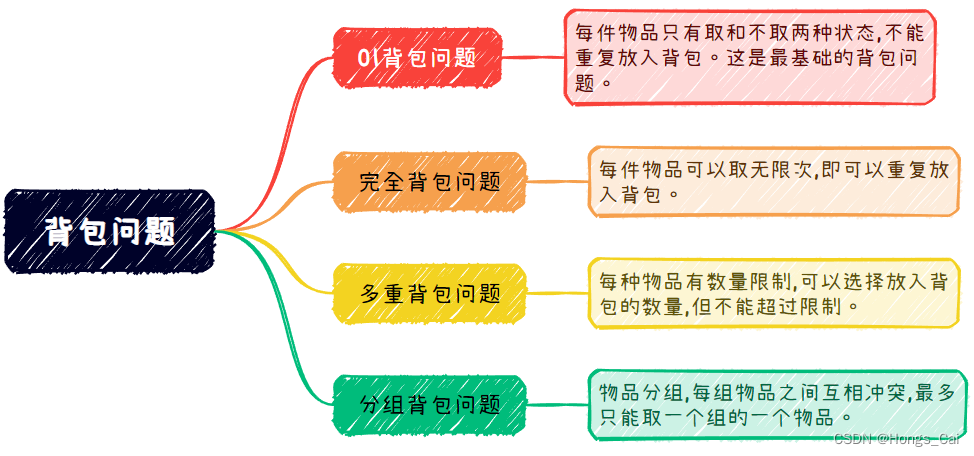
01背包
P2871 [USACO07DEC] Charm Bracelet S
01背包的板子题,大家应该都做过。
板子不应该是采药吗?
典型例题
题目描述:
有 \(N\) 件物品和一个容量是 \(V\) 的背包。每件物品只能使用一次。
第 \(i\) 件物品的体积是 \(v_i\),价值是 \(w_i\)。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式:
第一行两个整数,\(N\), \(V\), 用空格隔开,分别表示物品数量和背包容积。
接下来有 \(N\) 行,每行两个整数$ v_i$, \(w_i\),用空格隔开,分别表示第 \(i\) 件物品的体积和价值。
输出格式:
输出一个整数,表示最大价值。
数据范围:
0 < \(N , V\) ≤ 1000
0 < $v_i , w_i $≤ 1000
实现思路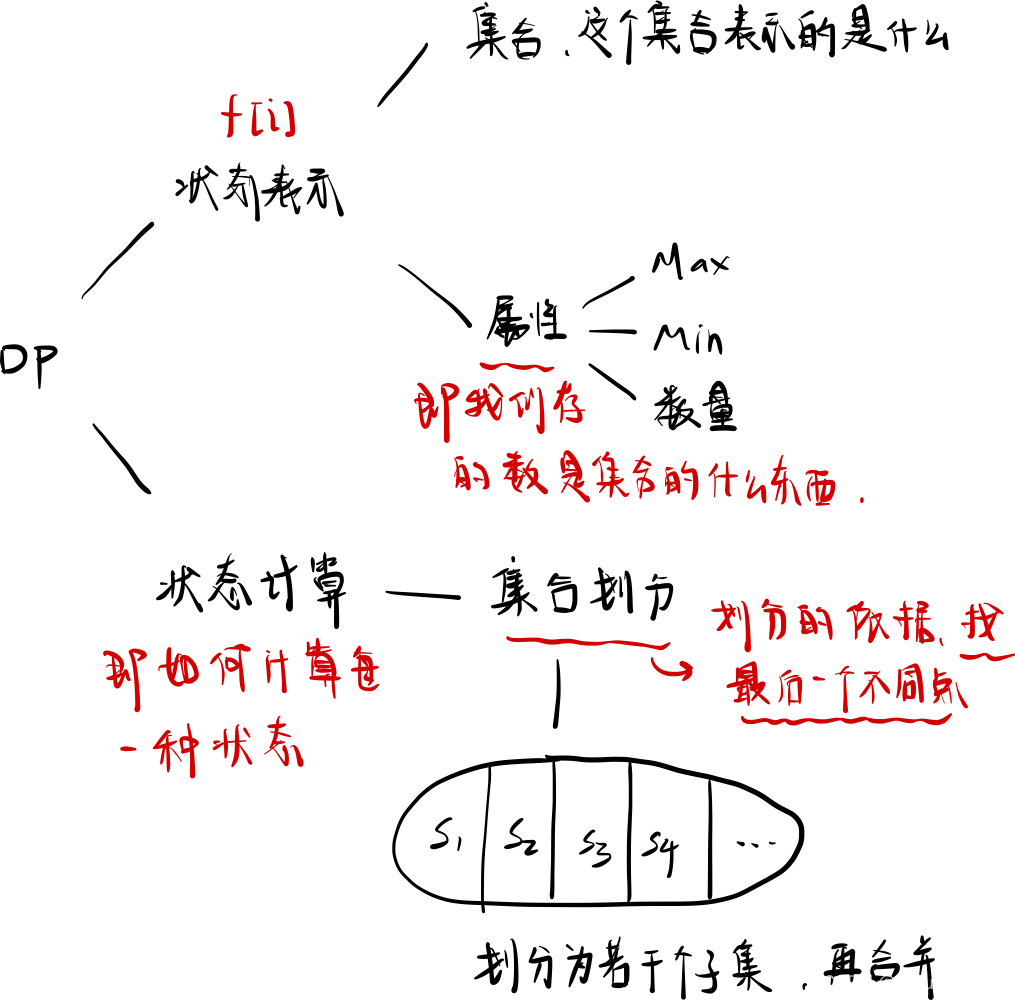
这里使用二维的状态表示 $f [ i ] [ j ] $,用来表示 只从前 \(i\) 件物品中选, 总体积 $\leq j $。
这样在状态计算中, 就可以把集合划分为$ f[ i − 1 ] [ j ] $(即只从前 $ i - 1 $ 件物品中选且不选择第 $ i $ 件物品), $ f[i - 1] [j - v[i]] + w[i] $( $v [ i ] $ 表示第 $ i $ 件物品的体积, \(w [i]\) 表示第 \(i\) 件物品的权重)(即只从前 $ i - 1 $ 件物品中选且选了第 $ i $ 件物品)。
通过以上思路可以得到状态转移方程:
$ \large f[i][j] = max(f [i - 1] [j],f[i - 1] [j - v[i]] + w[i]) $
完全背包
完全背包模型与 0-1 背包类似,与 0-1 背包的区别仅在于一个物品可以选取无限次,而非仅能选取一次。
所以完全背包主要在状态的计算方面有所不同,由于完全背包问题下所有可以选用的物品数量是无限的。因此状态转移方程为:$ f [i] [j]=max(f[i−1] [j],f [i−1] [j−v[i]]+w[i],...,f[i−1] [j−k∗v[i]]+k∗w[i]) \(
由于\) f [ i ] [ j − v [ i ] ] = m a x ( f [ i − 1 ] [ j − v [ i ] ] , f [ i − 1 ] [ j − 2 ∗ v [ i ] ] + w [ i ] , . . . , f [ i − 1 ] [ j − k ∗ v [ i ] ] + k ∗ w [ i ] ) $
为什么最后一项不是 \(f [ i − 1 ] [ j − ( k + 1 ) ∗ v [ i ] ] + ( k + 1 ) ∗ w [ i ] \)?
这是因为 $ k $ 的值只与背包最大容量相关
由上面两个公式我们可以推导出:
$ f [ i ] [ j ] = m a x ( f [ i − 1 ] [ j ] , f [ i ] [ j − v [ i ] ] ) $
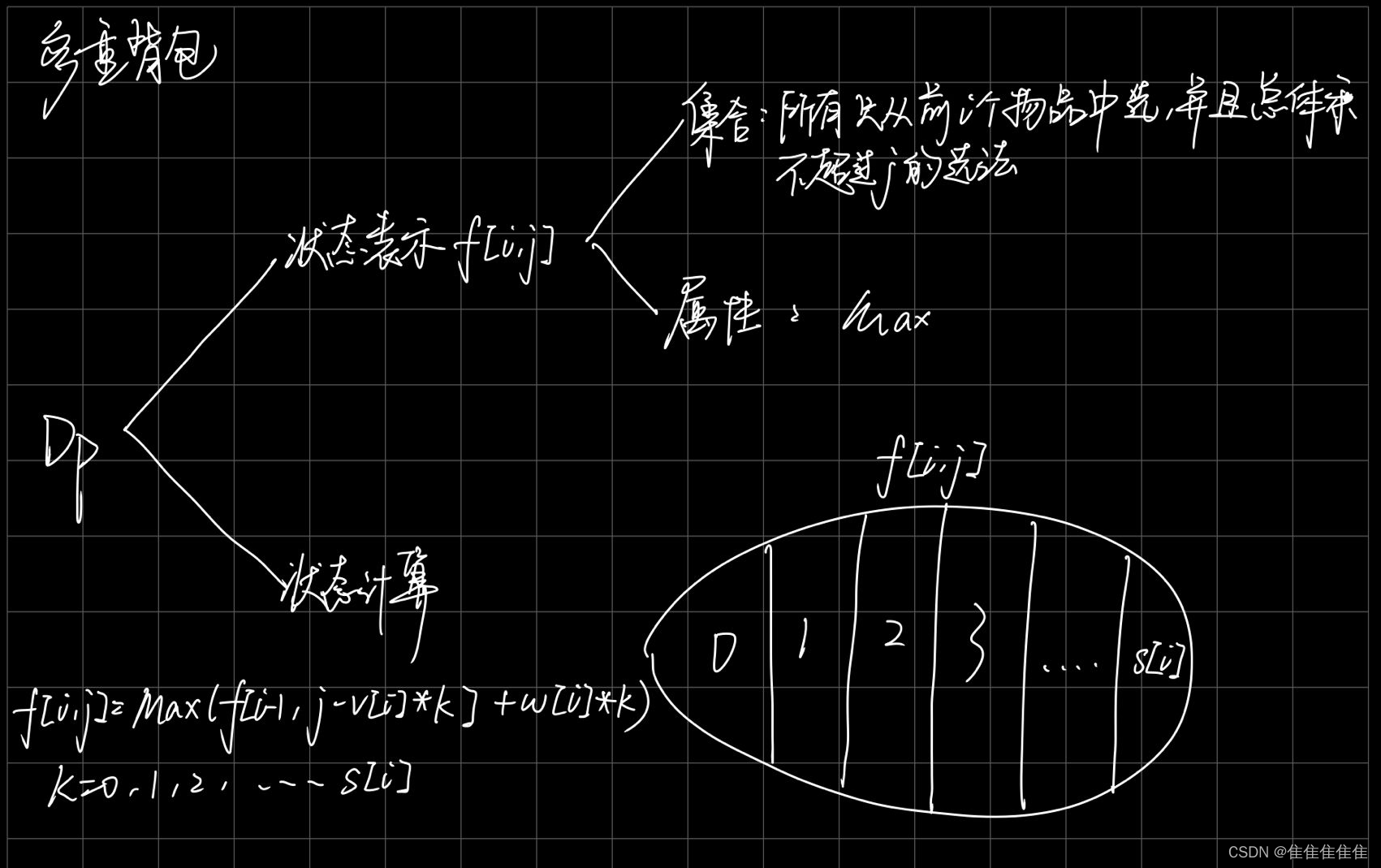
多重背包
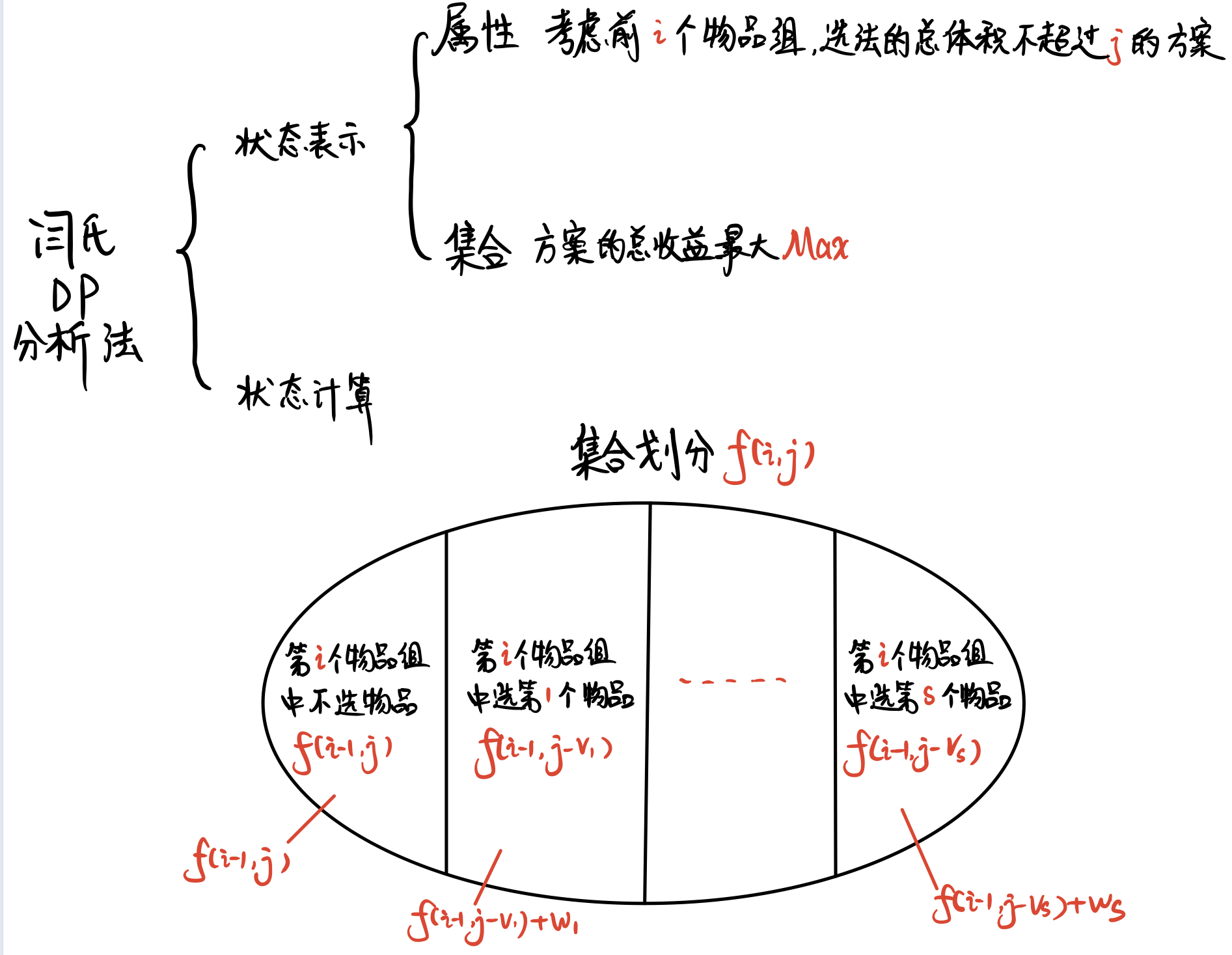
分组背包
区间DP
区间DP是一种动态规划算法,用于解决一些涉及区间的问题。区间DP通常需要定义一个二维的状态数组来表示区间的状态,其中状态转移方程往往与区间的划分有关。
具体来说,区间DP的状态通常表示为\(dp[i][j]\),表示区间\([i,j]\)的最优解或者其他需要求解的值。状态转移方程通常可以通过枚举区间内的一个点k来实现,即:
$dp[i][j] = min(dp[i][k] + dp[k+1][j] + cost[i][j]) $
或者
\(dp[i][j] = max(dp[i][k] * dp[k+1][j])\)
其中\(cost[i][j]\)表示区间\([i,j]\)的某种代价,可以是区间长度、区间权值和等。
通过这种方式,我们可以在\(O(n^3)\)或者\(O(n^4)\)的时间复杂度内解决一些区间相关的问题,比如最长回文子序列、最长公共子序列、字符串编辑距离等问题。
需要考虑不在环上,而在一条链上的情况。
令 \(f(i,j)\) 表示将区间 \([i,j]\) 内的所有石子合并到一起的最大得分。
写出 状态转移方程:
\(f(i,j)=\max\{f(i,k)+f(k+1,j)+\sum_{t=i}^{j} a_t \}~(i\le k<j)\)
令 \(sum_i\) 表示 \(a\) 数组的前缀和,状态转移方程变形为 \(f(i,j)=\max\{f(i,k)+f(k+1,j)+sum_j-sum_{i-1} \}\) 。
状压DP
通过将状态压缩为整数来达到优化转移的目的 julao
“状压 DP 是最直接的 DP ” —— dottle
状态压缩DP介绍
状态压缩DP其实是一种暴力的算法,因为它需要遍历每个状态,而每个状态是多个事件的集合,也就是以集合为状态,一个集合就是一个状态。集合问题一般是指数复杂度的NP问题,所以状态压缩DP的复杂度仍然是指数的,只能用于小规模问题的求解。
为了方便地同时表示一个状态的多个事件,状态一般用二进制数来表示。一个数就能表示一个状态,通常一个状态数据就是一个一串0和1组成的二进制数,每一位二进制数只有两种状态,比如说硬币的正反两面,10枚硬币的结果就可以用10位二进制数完全表示出来,每一个10位二进制数就表示了其中一种结果。
使用二进制数表示状态不仅缩小了数据存储空间,还能利用二进制数的位运算很方便地进行状态转移。
下面列举了一些常见的二进制位的变换操作。

The End.
本文来自博客园,作者:deviancez,转载请注明原文链接:https://www.cnblogs.com/deviance/articles/18172721


 浙公网安备 33010602011771号
浙公网安备 33010602011771号