机器学习 - 线性回归与逻辑回归（理论部分）
什么是线性回归？
根据样本数据的分布特点，通过线性关系模拟数据分布趋势，从而进行预测。对于下图来说，样本点的连线大致接近于一条直线，所以就可以将函数模拟成线性方程。
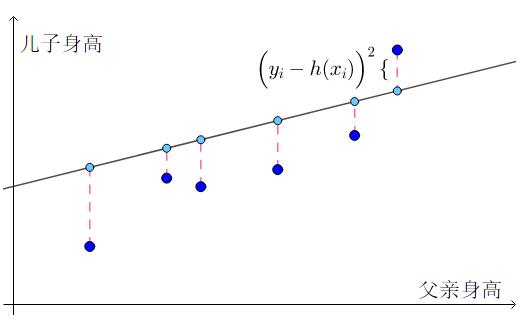
设 f(x) = wx + b，所以只要求出w 和 b，就可以得到x与y的关系，从而能够根据x预测出对应的y。
要求 w 和 b，只能借助于现有的数据样本。因为存在误差，这条直线不可能穿过所有的样本点，所以我们只需让误差最小即可。
如何描述误差(最小二乘法)
误差可以看做是对于相同的xi，通过模拟得到的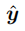
和真实的样本数据y的差。即
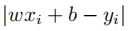。为了方便讨论，可以对绝对值求平方：
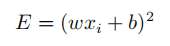
所以，只要求出所有样本真实值和预测值误差的最小值，就是误差最小的模拟。可用如下公式表示：
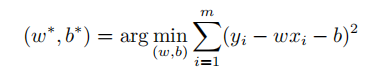
其中，w*、b*分别表示使得样本总体误差和最小的那组解。
我们在这里使用的是均方误差，它具有非常好的几何意义，通过欧几里得距离描述误差，显得非常直观。通过均方误差计算 w* 和 b* 的方法就叫做最小二乘法。
注：为什么不用样本点到直线的距离描述误差？
误差是一种相对概念，指样本真实值y与预测值f(x)的差，所以要基于相同的x。用点到线的距离的话，距离的直线和预测直线f(x)相交的点 与样本点没有可比性，这段距离无法解释误差的概念，所以基于相同的x更合适。
为了求目标函数的最小值，我们可以通过分别对w和b求导并等于0得到。求解过程如下 ：
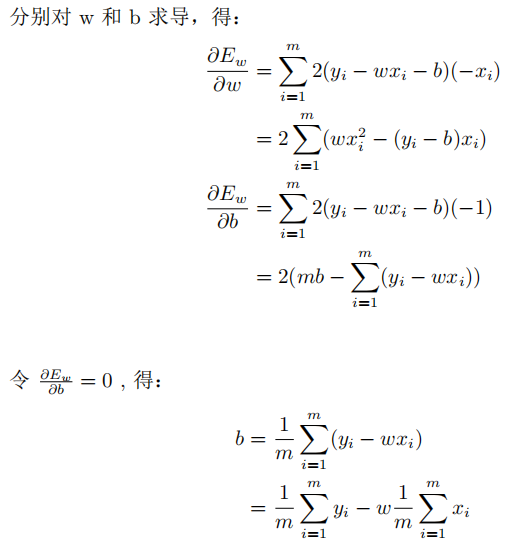
多项式回归
相对于直线而言，曲线肯定模拟的效果会更好，换句话说，也就是误差更小。以二次曲线为例，令f(w, b) = w2x^2 + w1x + b，则图像为：
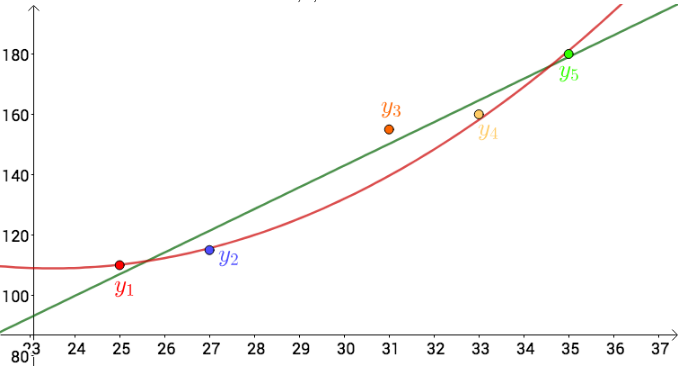
注：如果曲线的次数越高，说明f(w, b)值越精确(过于精确可能会导致过拟合的问题)。
可以看出，拟合的效果比直线更好些。
多项式回归的一般形式：
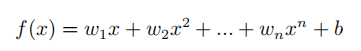
多项式回归的求解一般比较复杂，在工程上通常使用近似的方式求解，会用到梯度下降的方法，后面会讲到。
多元线性回归
上面讲的是特征只有一个的情况。多数情况下，一个事件的结果是由多种因素(特征)影响的。所以存在多个特征值的情况就叫做多元线性回归。
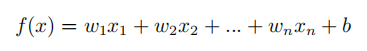
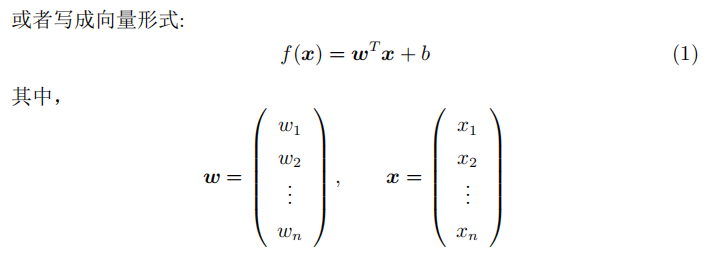
与之前的线性回归相似，我们可以利用最小二乘法对w和b进行近似。为方便推导，我们把整个数据集都使用向量表示：
其中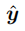表示样本的预测值。
可用于分类的逻辑回归
线性回归的模型告诉我们，样本的预测结果是连续的，输入一个x，总有一个模型中对应的y。如果y的值不是一系列的连续值，而是已知的几个结果，那就转化成了分类问题。
考虑一个最简单的二分类问题，掷硬币，我们一般会说，掷出正面或反面的概率都是1/2。所以，我们通常将分类问题转换为概率问题。如果P代表正面(y=1)的概率，P越大，y=1的概率越大；1-P则代表反面（y=0）的概率，P越小，y=0的概率越大。所以我们可以寻找一个边界，在这个边界的一边，全是y=1的正面点；另一边全是y=0的反面点。而靠近这个边界的点，则会表现出一定的随机性。
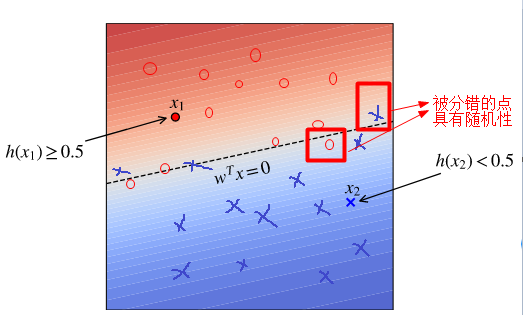
所以，我们需要找到一个值域为[0, 1]的函数，用来模拟预测模型，输入值为样本特征，输出值为对应分类的概率预测值。最直观的就是分段函数（也叫单位阶跃函数）：
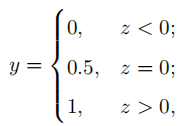
而通过该函数的分段函数可知，函数在x=0处不连续，所以，需要寻找一个替代函数，对数几率函数正是与单位阶跃函数相似的函数：
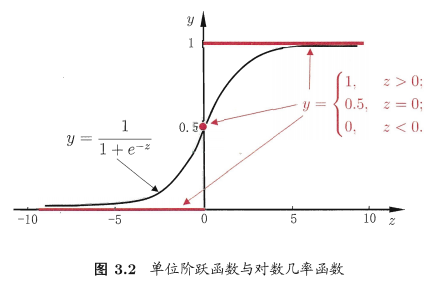
对数几率函数也叫做Sigmoid函数。
注：为什么会使用 Sigmoid 函数表示预测概率？
它是逻辑回归概率的另一种表现形式。可根据贝叶斯公式和全概率公式推导而出。
对于逻辑回归的二分类问题来说，每一次分类实际上都是一次伯努利实验(A分类或B分类)，如果假设每个分类下的样本属于正态分布，对于预测概率P(y=1|x)，可做如下推导：
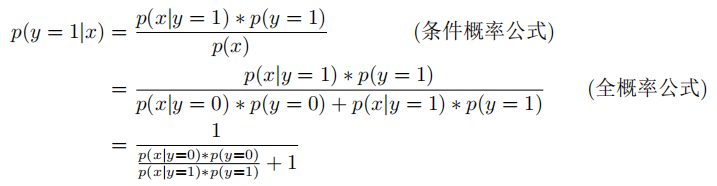
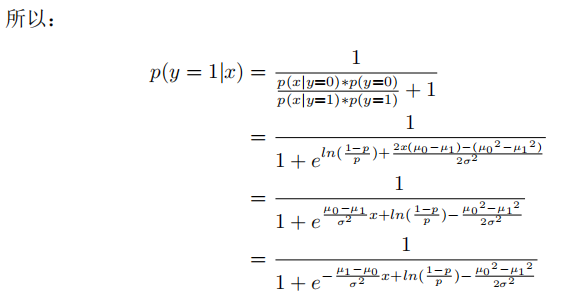
对于之前的假设条件：每个分类下的样本属于正态分布，可以这么理解。假设下图是某类人群的身高分布：
可以看出，整体是呈正态分布的，所以假设相对合理。
极大似然法
极大似然法的主要思想：概率最大的事情最容易发生，反过来说发生了的事情概率最大。当前的样本集既然出现了，说明它的概率就是最大的。所以我们只要求出当前样本集的联合概率的最大值，就能得到模型。所以我们设样本的联合概率为目标函数：
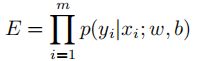
对右边取对数，并取负号，将求最大值转换为最小值：
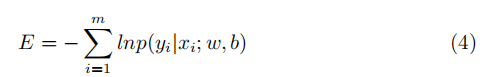
使用极大似然法推导目标函数
下面我们参照西瓜书对该目标函数进行推导。
假设x具有多元特征，则有：
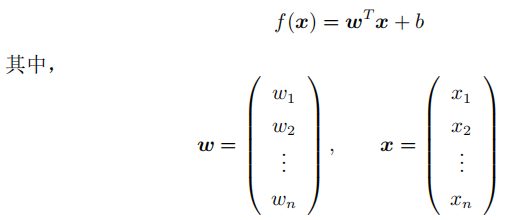
带入二分类的概率公式，得：
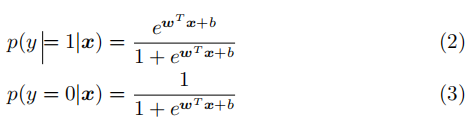
注：此处没有用之前推导出的Sigmoid函数，使用的是西瓜书上3.23和3.24的公式(p(y=1)和p(y=0)的公式相反)，是为了推导出与之一致的结果，实际上原理是相同的。
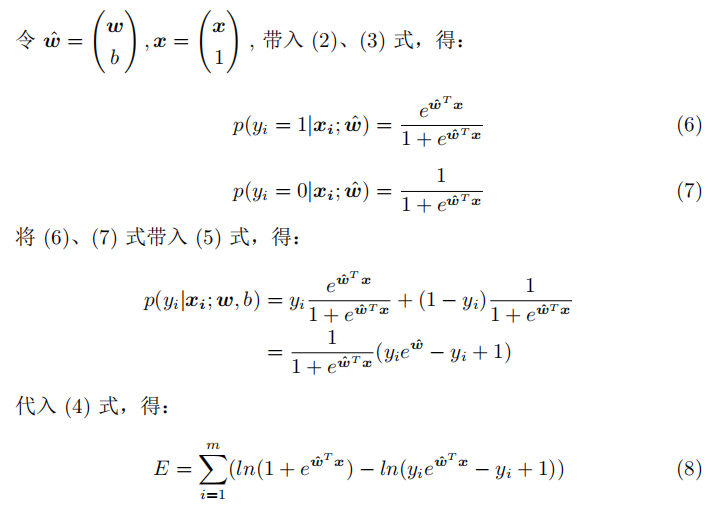
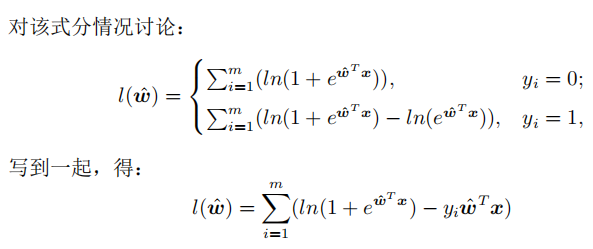
使用交叉熵推导目标函数
我们直到信息熵是用来度量某一特定样本集分布的纯度（或者混乱程度/不确定性），信息熵越大，纯度越低（混乱程度/不确定性越高），公式如下：
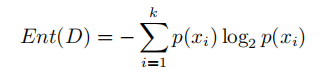
而交叉熵则是考察两个样本集，度量这两个样本集的差异。交叉熵越大，代表两个分布的差异越大，反之越小。
凸函数及梯度下降法
至此，我们就最大限度地推导了逻辑回归的目标函数。那么接下来我们能否仿照线性回归那样，直接对目标函数求导，通过令一阶导数为零直接求解出最优解
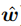呢？其实从公式（10）可以看出，这是一个关于的高阶非线性函数，直接求一阶导数的解将非常复杂。所以我们将使用凸优化理论中的经典数值优化算法——梯度下降法。但是，能使用这种优化算法的前提是函数是凸函数。
凸函数的证明
关于凸函数，有如下定理：
翻译一下就是：
所以，我们就是要证明目标函数的海塞矩阵为半正定矩阵。海塞矩阵即由目标函数对向量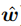各分量的二阶偏导数所组成的矩阵：
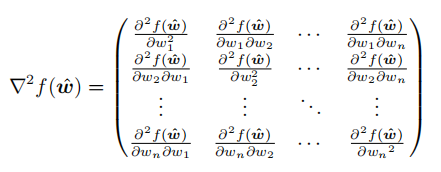
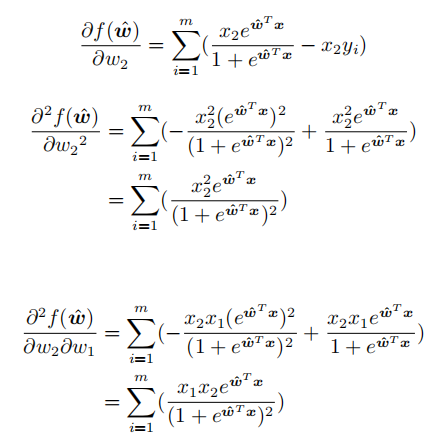
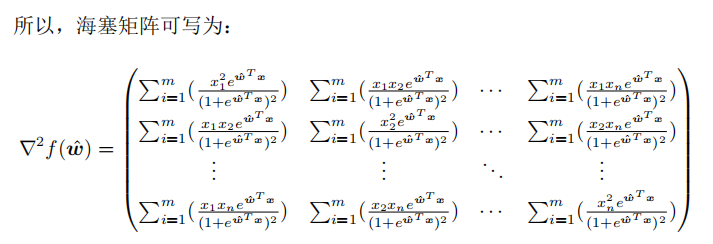
梯度下降法
证明了目标函数为凸函数后，就可以使用梯度下降法求极值了。那什么是梯度呢？梯度就是使方向导数最大的方向。那什么又是方向导数呢？在多元函数中，我们沿函数图像上某一点做切线，可以有无数种选择，因为沿任意方向都可以做该点的切线。我们需要从中找到一个方向，能使函数的变化值最大，这就是梯度。
注：关于梯度的详细解释，可以参考这篇文章：《梯度的方向为什么是函数值增加最快的方向？》
我们还可以从微分的角度理解：
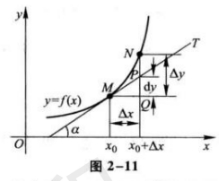
当N点逐渐靠近M点，即△x足够小时，我们可以将曲线MN近似为直线MN，所以tanα ≈ △y/△x。所以有：
\(\Delta{y} \approx \Delta{x} * tan{\alpha}\)
而
\(\Delta{y} = f(x_0 + \Delta{x}) - f(x)\)
\(tan(\alpha) = \frac{\partial{f(x_0)}}{\partial{x}}\)
所以：
\(f(x_0 + \Delta{x}) \approx f(x) + \Delta{x}\frac{\partial{f(x_0)}}{\partial{x}}\)
上式也等价于：
\(\Delta\smash{f(x)} \approx \Delta{x}\frac{\partial{f(x_0)}}{\partial{x}}\)
如果我们要找 \(f(x)\) 的最小值，就需要保证 \(\Delta\smash{f(x)} \le 0\)，\(f(x)\) 才会不断减小。可以观察出，当 \(\Delta{x} = -\eta\frac{\partial{f(x_0)}}{\partial{x}}\) 时，\(\Delta\smash{f(x)} \approx -\eta(\frac{\partial{f(x_0)}}{\partial{x}})^2 \le 0\) 恒成立。
将 \(\Delta{x} = -\eta\frac{\partial{f(x_0)}}{\partial{x}}\) 写成一般情况下的式子：
\(\bm{x_{n+1} = x_{n} - \eta\frac{\partial{f(x_{n})}}{\partial{x}}}\)
只要我们使用这个公式，不断地更新 \(x\)，就可以接近最小值（在机器学习中，更习惯使用 \(\bm{w}\) 或者 \(\bm{\theta}\) 表示多维向量）。
（实际上，\(\Delta{x} = -\eta\frac{\partial{f(x_0)}}{\partial{x}}\) 这个式子也解释了为什么要沿梯度的反方向。）
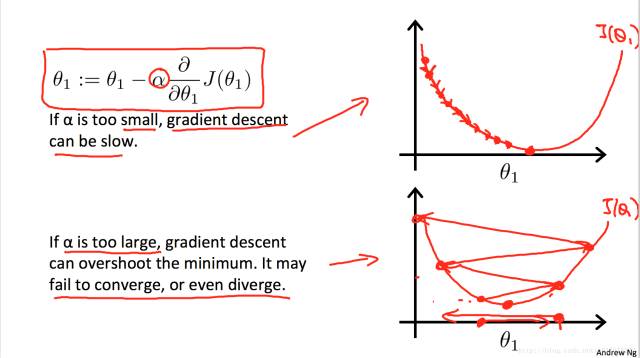
这里的 \(\eta\) 在机器学习中也叫做学习率，就是每走一步的跨度。它是一个超参数，需要人为进行设定。对学习率的设定，需要注意，如果设置得太小，则可能会经过非常多的迭代次数才能接近最小值，消耗过多的资源；但如果设置得太大，则可能直接跨过最小值，甚至逐渐偏离：
