lxl 海亮讲课

例题1：非公开题目

题意

每个位置上有一个容量为 \(b_i\) 的背包，每次插入物品超过容量会弹出最早的物品。

两种操作：

• \([l,r]\) 都插入大小为 \(x\) 的物品
• 查询 \(p\) 位置背包有多少物品

做法

化成二维平面 时间-序列。顺着序列方向做扫描线，用线段树维护所有时间上增加的物品，每次查询线段树上二分出一个后缀即可。

值域倍增分块（分组）

带 \(\log\) 复杂度的均摊。

可以解决一些值域相关的区间问题。

例题2：洛谷 P7447

将值域分为 \([2^0,2^1)\), \([2^1,2^2)\), …, \([2^{k-1},2^k)\) 这 \(\log n\) 块。每个块用普通线段树维护 sum、max 和 min。每次操作：

• 对于不包含 \(x\) 的大于 \(x\) 的块，不断找出块的 \(\min\) 放到下面的块直到 \(\min\) 不会因 \(-x\) 被放到下面的块。
• 对包含 \(x\) 的块不断把上方 \(\max\) 往下放直到 \(\max \le x\)（\(\max >x\) 的一定会往下放，因为它被减去了一半以上）。

---

例题3：CF1515I Phoenix and Dimonds

注意同种钻石不能拆分。

对价值进行分块，按 \(c\) 价值从大到小处理。用线段树二分出能取得的最多钻石总数，然后往下跳。

具体细节不清楚。

线段树维护括号匹配

例题4：QOJ #8227. PKUWC2024D2T3 栈

化为 时间-位置 二维平面关于位置做扫描线。

把栈问题转换为括号匹配（可孤立右括号版）。

Trick. lxl：括号序列/栈问题能差分成后缀的一定要差分。不要查区间。查区间必死（复杂度会爆，检查，但也有做法参见P6781）。 要维护已被匹配的括号的总和。

从一个点出发保留区间的连通块

洛谷 P5311 [Ynoi2011] 成都七中

假设 x 不变化。于一个 x，与之联通的点 p 满足：p到x的路径上 \(l\le min,r\ge max\) 。将一条路径的min和max放到二维平面上，则一个 l,r 会查询一个右上角的 2-side 矩形中不同元素个数。

那么我们把询问变成点，然后对于每种颜色，统计它们贡献到的询问，也就是它们左下方矩形包含询问的并的大小。

2-side矩形（1/4矩形）的并集 -> 4-side矩形的和；我们单调队列切分为若干不重复的块即可。

如果 x 变化，做一个淀粉质。若对于一次询问，x与当前重心联通，则把重心当做 x 做这个问题，否则只需递归进入 x 所在子树内计算答案即可。

总的来说：

• 若 \(x\) 与当前重心联通，统计颜色在矩形 \([l, +\infty) \times (-\infty, r]\) 内的出现次数。
• 复杂度 \(\mathcal{O}(n \log^2 n)\)，空间 \(\mathcal{O}(n)\)。

例题：未公开题目

一棵树，每个点有颜色，每次查询只保留某种颜色的点的情况下，连通块大小。（？

没听见。

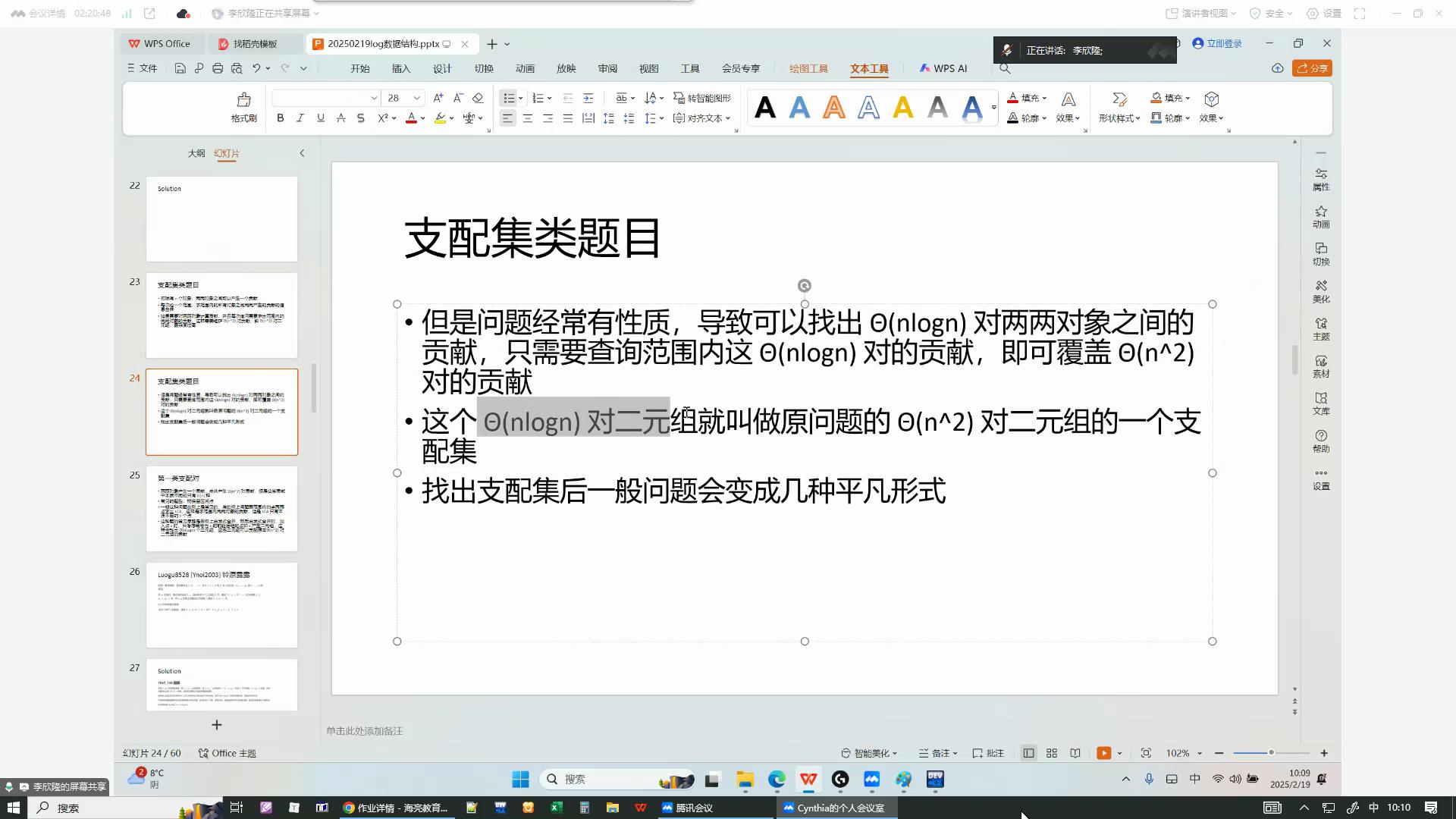
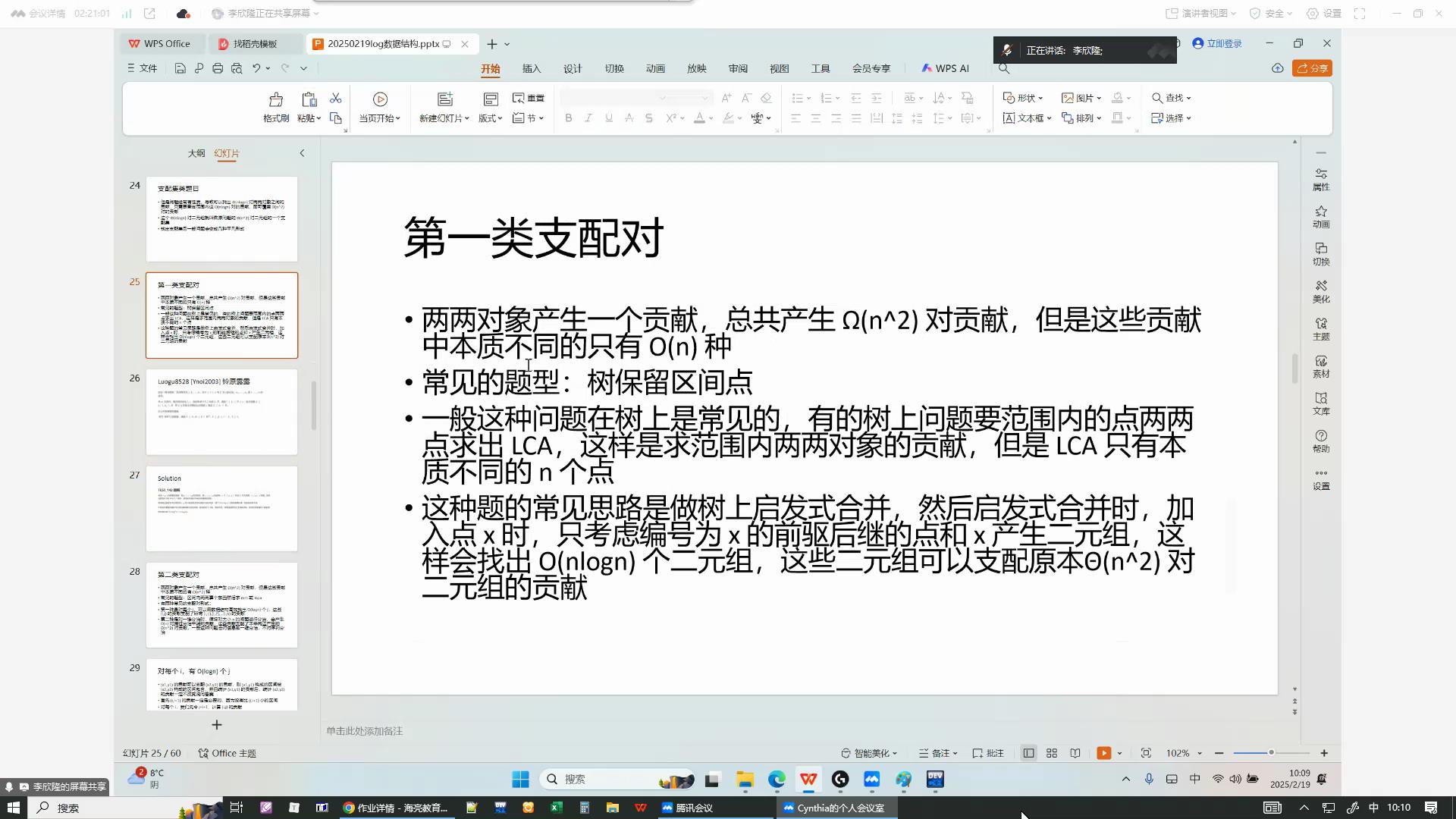
支配集类题目

P8528 [Ynoi2003] 铃原露露

CodeChef MINXORSEG

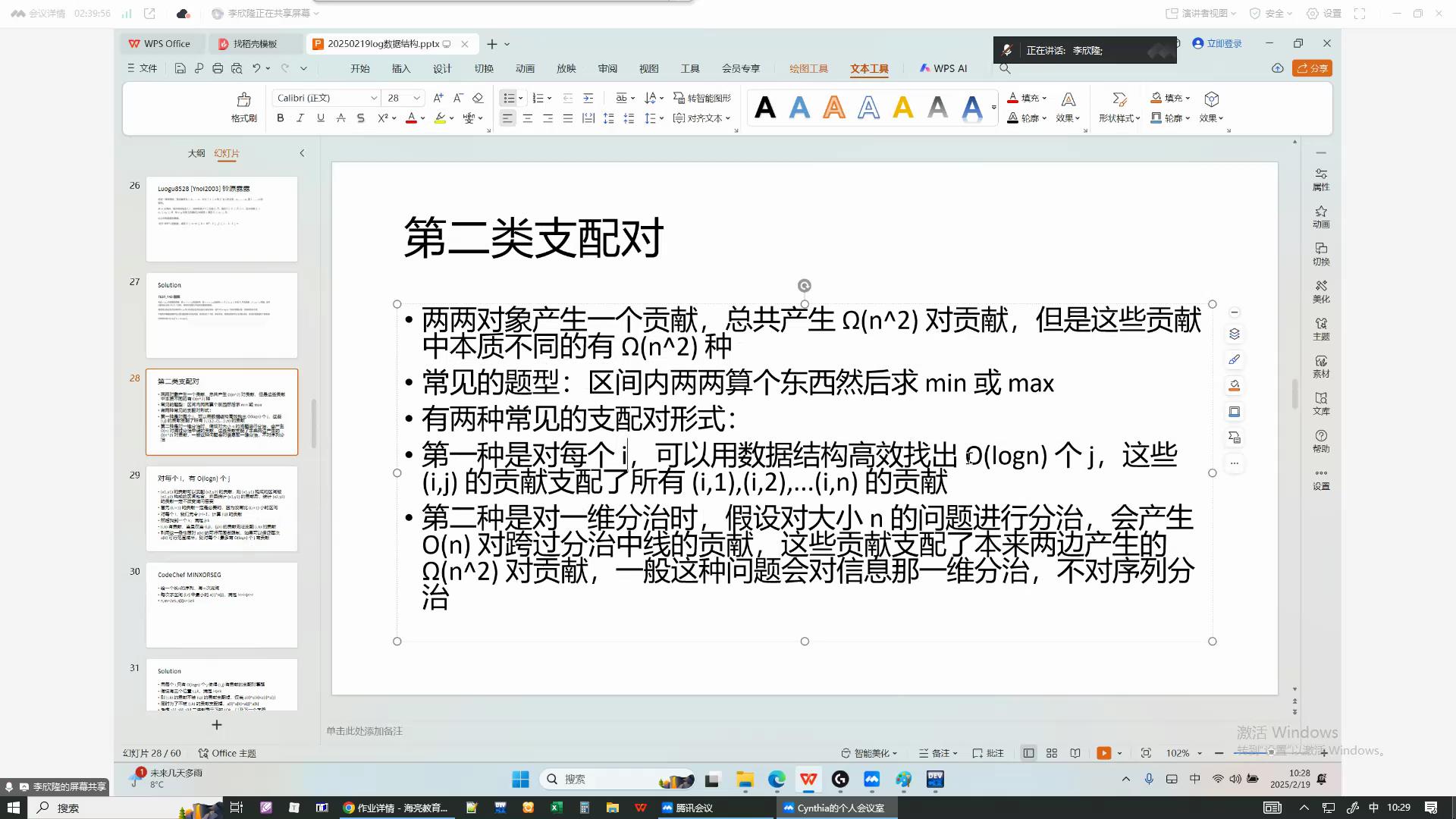
未公开题目

给定长为 \(n\) 的序列 \(a\) 和正整数 \(d\)，定义一个区间 \([l,r]\) 是好的，当且仅当 \(a_l\dots a_r\) 升序排列后相邻两数之差不超过 \(d\)。现有 \(q\) 次询问，每次给定 \(L,R\)，问有多少 \([L,R]\) 的子区间 \([l,r]\subset[L,R]\) 是好的.

定义差小于等于 d 的两个数是联通的。因为不是树，不能用点点边法。用代表元法，以一个数代表一个连通块。

P7126 [Ynoi2008]rdCcot & THUWC2020 某科学的动态仙人掌

注意到同一个 C块 往上跳 c/2 次一定会跳到同一个点，我们以这个点为代表元。

考虑画一个数轴。

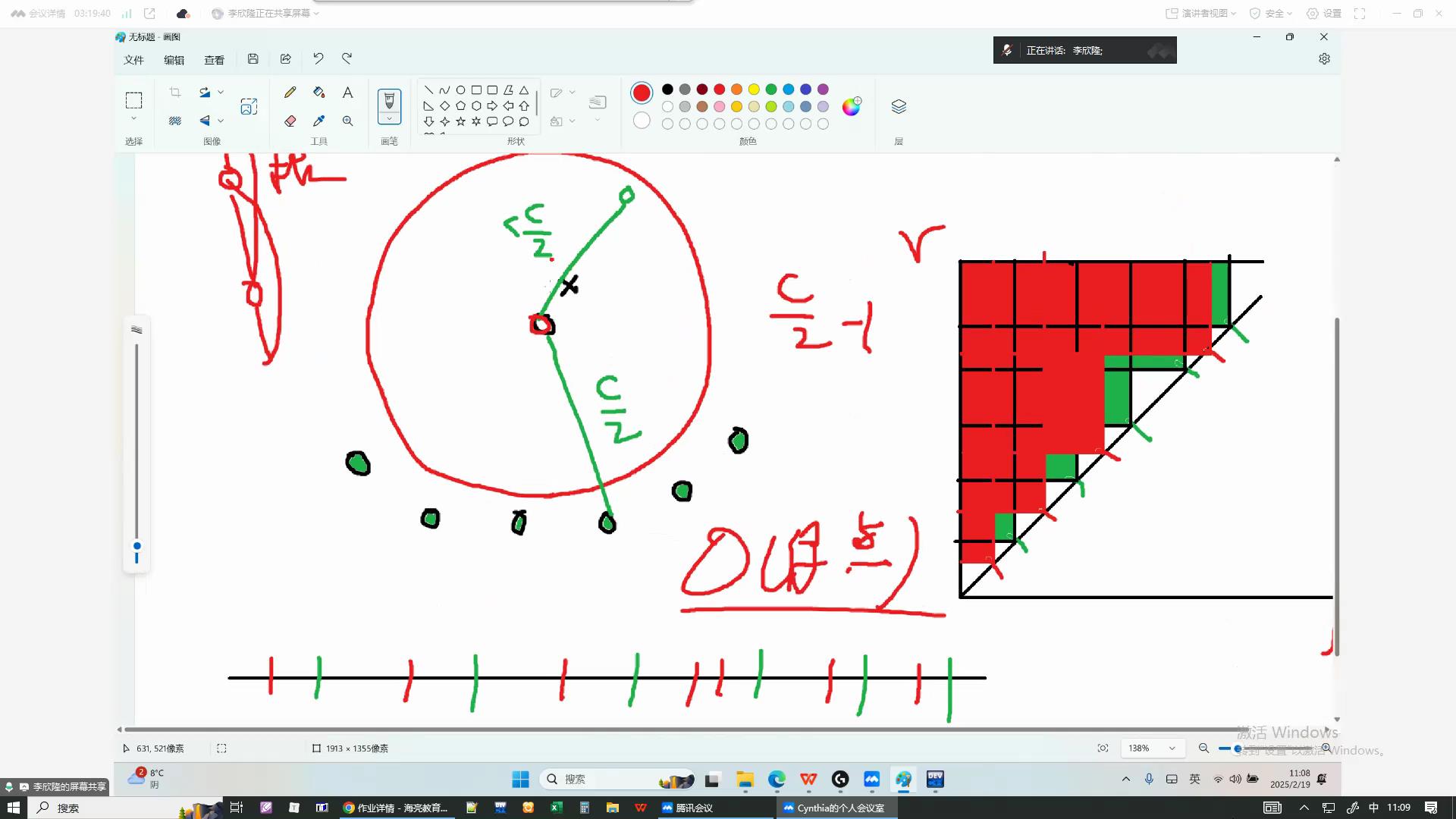
例题

P11695