[AtCoder Iroha2019 Day4 L] 好きです 题解

[AtCoder Iroha2019 Day4 L] 好きです 题解

先考虑静态问题。先把绝对值拆开，只考虑询问左边的点，反过来的情况类似。容易想到在平面直角坐标系上考虑。考虑每个点对答案的贡献。对于点 \((x, y)\) 和询问 \(x_{0} > x\)，这个点对答案的贡献相当于使答案对 \(\dfrac{y}{x_{0} - x}\) 取 \(\max\)。把一个点的贡献看作关于 \(x_{0}\) 的函数，则相当于平面有若干个函数图象，每个点 \((x_{0}, 0)\) 的答案就是它正上方的点中纵坐标最大的。\(x_{0}\) 在分母不好做，所以取个倒数变成 \(\dfrac{x_{0} - x}{y}\)，这是关于 \(x_{0}\) 的一次函数

\[\dfrac{1}{y} x_{0} - \dfrac{x}{y} \]

于是问题就变成了：

平面上有若干条直线，多次给定 \(x_{0}\)，求出直线上的点中，横坐标为 \(x_{0}\) 的点中纵坐标为正数且最小的。

把操作和询问的 \(x\) 坐标一起从小到大排序（操作的 \(x\) 相当于对应直线的零点），逐个处理。维护加入直线的最小值构成的函数。这么做保证了考虑到的直线在 \(x = x_0\) 处一定为正。由于一次函数是上凸的，根据经典结论，一堆一次函数的 \(\min\) 仍然上凸，所以直线的最小值构成一个上凸包：

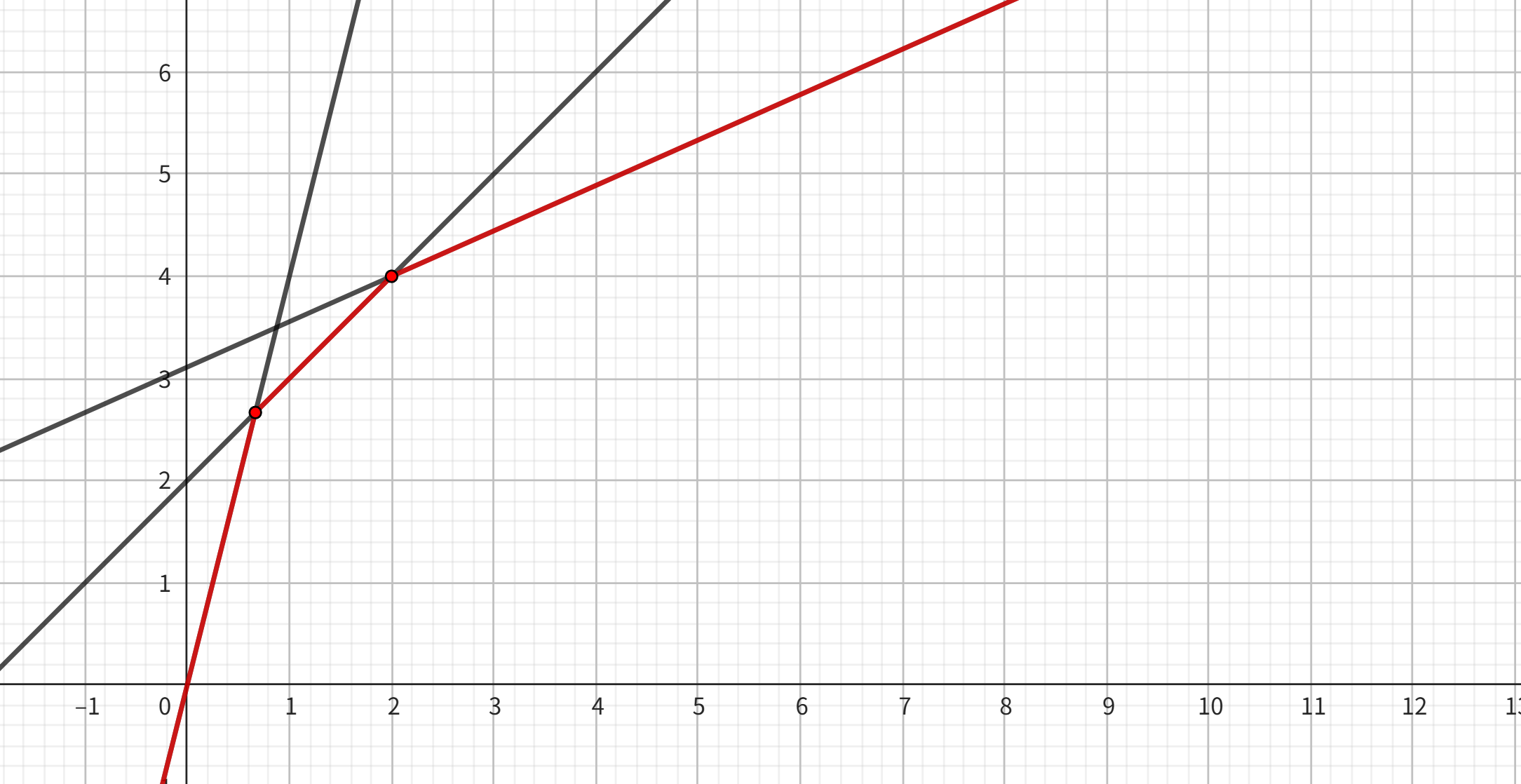
注意到上凸包有以下性质：

• 随着 \(x\) 坐标的增大，使得 \(y\) 最小的直线斜率单调递减。

所以我们考虑维护一个单调栈，从栈底到栈顶从小到大存放直线的斜率，并且保证栈中每一条直线都存在某个位置，使得这堆直线中的最小值在此直线取到（也就是说保证每条直线都是凸包的一部分）。

加入一条新直线 \(l\) 时，讨论它与栈顶直线的关系。有两种情况：

1. \(l\) 的斜率小于等于栈顶直线的斜率。由于已经把直线的零点和询问的 \(x\) 坐标从小到大排序，所以对于 \(x\) 坐标更大的询问，\(l\) 的纵坐标都一定小于斜率更大直线的纵坐标。此时连续弹栈，直到栈顶直线斜率小于 \(l\) 的斜率。

   

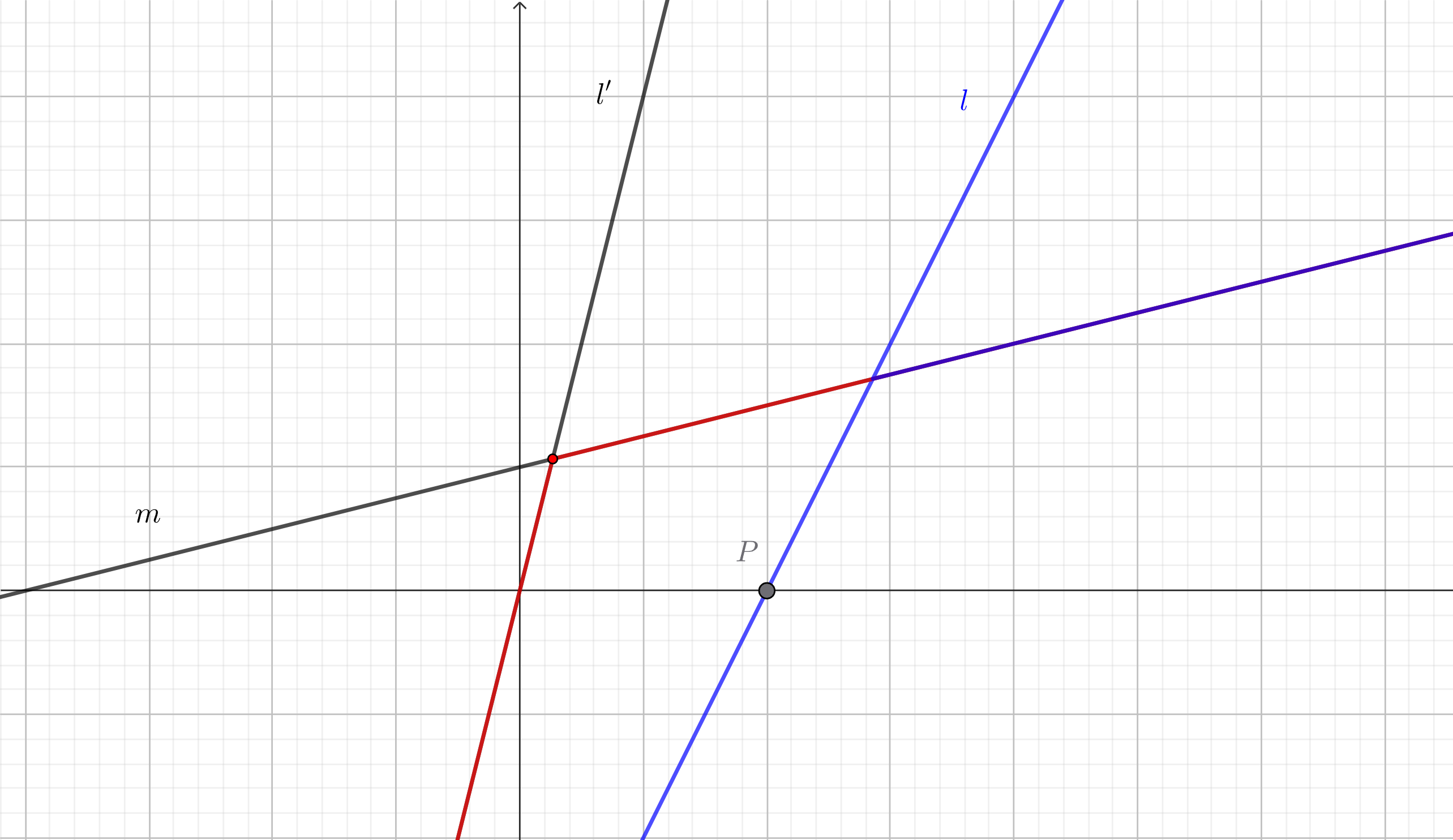
   如图，\(l\) 是新加入的直线。由于 \(l\) 的斜率小于 \(l'\) 的斜率，所以对于 \(P\) 点右侧的询问，\(l\) 的纵坐标一定小于 \(l'\) 的纵坐标，因此 \(l'\) 被弹出。但直线 \(m\) 被保留了。

2. \(l\) 的斜率大于栈顶直线的斜率，但是 \(l\) 与栈顶的交点在栈顶与次栈顶的交点右侧。

   

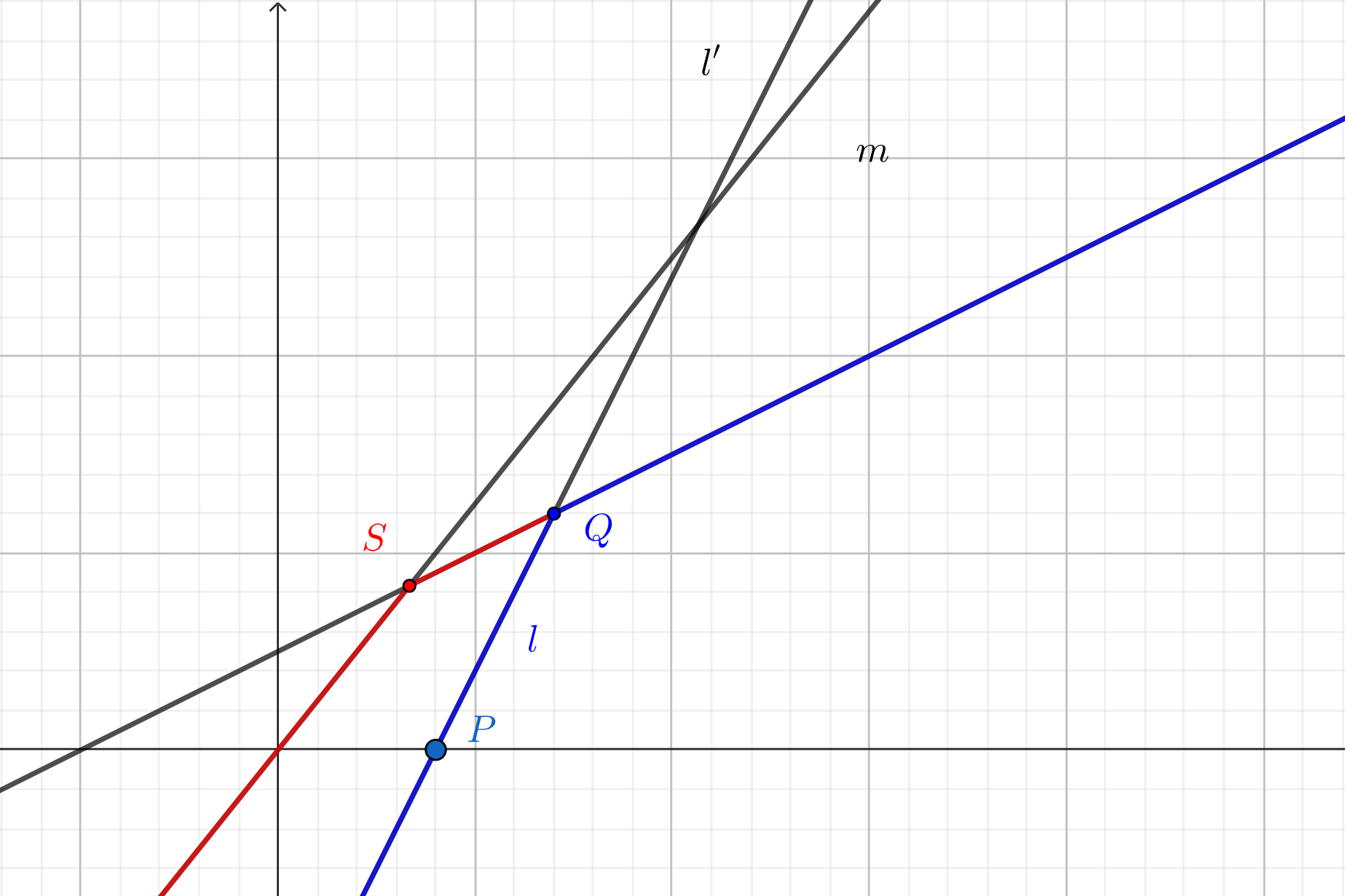
   如图，虽然 \(l\) 的斜率大于栈顶 \(l'\) 的斜率，但是由于 \(l\) 和 \(l'\) 的交点 \(Q\) 在 \(l'\) 与 \(m\) 的交点 \(S\) 左侧，所以对于 \(P\) 右侧的询问，纵坐标最小值不可能在 \(l'\) 取到，这种情况我们也需要弹栈。

以上就讨论完了加入直线的情况。下面考虑如何处理询问。根据凸包的性质，随着 \(x\) 坐标的增大，使得 \(y\) 最小的直线斜率单调递减。而栈中的直线斜率已经有序，且询问的 \(x_0\) 也有序，所以只要比较栈顶和次栈顶在 \(x_0\) 处的纵坐标哪个小，如果次栈顶更小，就弹栈。重复这个过程知道栈顶在 \(x_0\) 处纵坐标最小，此时栈顶的纵坐标就是答案。

现在静态问题就解决了，时间复杂度为 \(O(n \log n)\)，瓶颈在排序，计算答案的过程是线性的。下面考虑动态问题。

对时间轴建立线段树。还是把操作和询问按 \(x\) 坐标排序，然后预处理出每条直线出现的时间区间 \([l, r]\)，对于 \([l, r]\) 在线段树上拆分出的 \(O(\log n)\) 个区间，把直线加入到这个区间内，按静态问题的方法维护每个区间的凸包。查询 \(x_{0}\) 时，对于线段树上包含 \(x_{0}\) 的 \(O(\log n)\) 个区间，分别计算答案然后取 \(\min\)。由于 \(x\) 坐标有序，所以正确性可以保证。至于时间复杂度，每条直线在 \(O(\log n)\) 个线段树上的区间出现，所以所有区间直线的总数为 \(O(\log n)\)。用单调栈计算答案的过程是线性的，所以总时间复杂度还是 \(O(n \log n)\)。

代码实现非常清晰：Code

下面附上我写的 generator 供大家调试，可以自行修改数据范围。为了方便，使用了 vector.erase() 用来完成从 set 中随机选取元素的过程，时间复杂度比较劣，但实测生成大数据也很快。（实际上更好的做法是把删除的元素和 vector.back() 交换，然后 pop_back()。）

generator

#include<bits/stdc++.h>

using namespace std;

constexpr int n = 30, w = 100;
mt19937 rng((int)chrono::system_clock::now().time_since_epoch().count());
// mt19937 rng;
uniform_int_distribution<> dis_op(1, 3), dis_x(-w, w), dis_y(1, w);

int main() {
    cin.tie(nullptr) -> sync_with_stdio(false);

    cout << n << '\n';

    multiset<int> vis;
    vector<int> pt_id, pt_x(1);
    int cnt = 0;

    for(int i = 1; i <= n; i++) {
        int op = dis_op(rng);
        if(pt_id.empty() && op == 2) op = (rng() & 1) ? 1 : 3;
        cout << op << ' ';

        if(op == 1) {
            int x = dis_x(rng), y = dis_y(rng);
            pt_id.push_back(++cnt), pt_x.push_back(x);
            vis.insert(x);
            cout << x << ' ' << y << '\n';
        } else if(op == 2) {
            assert(!pt_id.empty());
            int m = (int)pt_id.size();
            uniform_int_distribution<> dis_k(0, m - 1);

            int k = dis_k(rng);
            cout << pt_id[k] << '\n';

            assert(vis.count(pt_x[pt_id[k]]));
            vis.erase(vis.find(pt_x[pt_id[k]]));
            pt_id.erase(pt_id.begin() + k);
        } else if(op == 3) {
            int x = dis_x(rng);
            while(vis.count(x)) {
                x = dis_x(rng);
            }
            cout << x << '\n';
        }
    }

    return 0;
}