卷积操作的线性性质

(离散)卷积操作其实是仿射变换的一种: 对输入向量进行线性变换, 再加一个bias. 是一种线性变换. 它本身也满足线性函数的定义.

它可以被写成矩阵乘法形式. 以下图的卷积操作为例:

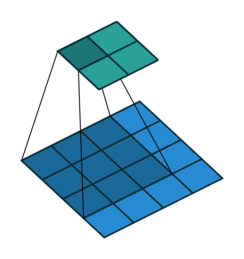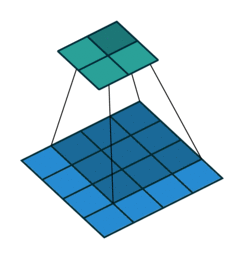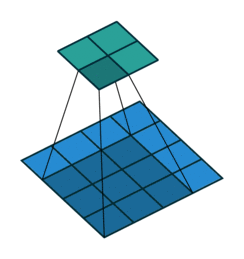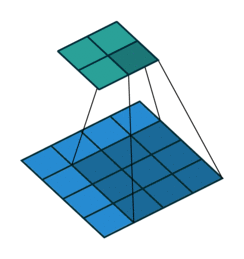
若将\(3\times 3\)的卷积核与\(4\times 4\)的输入都按行优先展开为一维列向量. 则定义在它们之上的卷积操作可以写为矩阵\(C\)与向量\(x\)的乘法. \(C^T\)为:

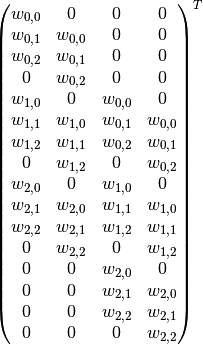
\(C\)定义了网络的连接矩阵/拓扑结构. 从这个角度去看, 卷积网络跟MLP在本质上是相同的, 只不过卷积网络的神经元共享了很多参数.