zjk 串串

这下是真学懂了。

this is true algorithm.

kmp

现在有这样一个问题：给定一个模式串 \(T\) 和文本串 \(S\)，现在要求 \(T\) 在 \(S\) 中出现了多少次。

暴力的做法是对着每一个 \(i\) 都去判断一下是否可以匹配得上，我们考虑优化这一过程：

假设我们已经考虑了 \(S\) 的前 \(i\) 位，现在已经匹配上了 \(T\) 的前 \(len\) 位，那么匹配状况就如下图所示：

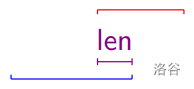
蓝色的是 \(S\) 的一段前缀，红色是一整个 \(T\)。

现在考虑从 \(i \to i+1\)，这时候讨论一下：

如果 \(S_{i+1}=T_{len+1}\) 直接 \(len+1\)。

那么如果 \(S_{i+1}\) 和 \(T_{len+1}\) 不相等，这时我们似乎就该把 \(len\) 设成 \(0\) 重新考虑了。

这是不对的，我们这时需要找到最长 \(T_{1:len}\) 这个前缀上的一个最长后缀使得它可以和 \(T_{1:len}\) 的某个前缀匹配上，我们记这个长度为 \(fail_{len}\)。

那么我们只需要一直跳 \(fail\) 直到有一个 \(fail\) 可以刚好加入 \(S_{i+1}\) 这一位就行，这显然是正确的。

时间复杂度直接势能分析，注意到势能只会在 \(i\to i+1\) 的时候加一，所以总的势能是 \(n\)，最坏也就被减去 \(n\) 次。

AC 自动机

上面解决的是一个文本串和一个模式串，现在增多这个模式串的数量。

那么我们更新一下这个 \(fail\) 的定义：

对于一个模式串 \(T_{i,1:len}\) 的前缀，找到任意一个 \(T_{i,1:len}\) 最长的后缀使得可以被某个 \(T_{j}\) 的前缀给匹配上，\(fail\) 指向这个前缀。

然后定义一个 \(nxt_{i,c}\) 为状态转移边，表示 \(T_{1:len}(i)\) 这个状态添上一个 \(c\) 字符后能找到的一段最大的一段后缀使得它能够匹配上某个 \(T_j\) 的前缀，指向这个前缀。

维护一堆串的前缀？直接给你扔到 trie 树上去，然后现在就是要对着一棵已知的 trie 树求他的 fail 指针了，这里考虑使用 bfs 去求。

对于一个 \(i\) 状态，分类：

如果其有 \(c\) 这条边，那么 \(nxt_{i,c}\) 就是原 trie 树的边，\(nxt_{i,c}\) 的 \(fail\) 按理来说我们要一直从 \(i\) 这一直跳 \(fail\)，跳到一个有 \(c\) 这个儿子的为止。

但是我们是 bfs ，这时我们已经求出了 \(nxt_{fail_{i},c}\) 这条转移边，所以直接 \(fail_{nxt_{i,c}}=nxt_{fail_{i},c}\) 就行。

如果没有 \(c\) 这条边，一样的，我们已经知道了 \(nxt_{fail_{i},c}\) 的转移边，也是直接 \(nxt_{i,c}=nxt_{fail_{i},c}\) 就行。

一些子串问题

我们现在要求一堆模式串在文本串出现了多少次，首先对这些模式串建立 ac 自动机。

然后我们根据这个文本串在这个自动机上走，走到的一个地方给这个地方的经过次数加一，跑完了过后我们就统计了部分前缀的出现次数，因为有些前缀会把其他的前缀的贡献给盖掉，但我们要的是所有前缀的出现次数阿。

注意到 \(i\to fail_i\) 相当于是对一个 \(i\) 状态求它的一个后缀，前缀的后缀不就是子串吗。

所以你对这个 \(fail_i \to i\) 建树，求个子树和就是正确的出现次数了。