AtCoder Regular Contest 203 (Div. 2)
ARC203A All Winners
如果一个人不是全胜的话,完全是可以让他全败的。
所以可以每组钦定一个人赢,一个人输,每组赢的人把其他组输的人全杀了,这样就实现了上面的东西,会有 \(\displaystyle \left\lfloor \frac{nm}{2} \right\rfloor\) 个人全胜。
如果 \(m\) 是奇数的话,此时每组还剩下一个人,显然可以额外调出一个人全胜。
int main() {
#ifdef LOCAL
freopen("!in.in", "r", stdin);
freopen("!out.out", "w", stdout);
#endif
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int T;
std::cin >> T;
while (T --) {
int n, m;
std::cin >> n >> m;
std::cout << 1LL * m / 2 * n + m % 2 << '\n';
}
return 0;
}
ARC203B Swap If Equal Sum
本质不同的操作只有两种:交换 \(\texttt{01}\) 和 \(\texttt{10}\),交换 \(\texttt{00}\) 和 \(\texttt{0}\)。
int main() {
#ifdef LOCAL
freopen("!in.in", "r", stdin);
freopen("!out.out", "w", stdout);
#endif
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int T;
std::cin >> T;
while (T --) {
int n;
std::cin >> n;
std::vector<int> a(n), b(n);
for (int i = 0; i < n; i ++) {
std::cin >> a[i];
}
for (int i = 0; i < n; i ++) {
std::cin >> b[i];
}
const int sA = std::count(a.begin(), a.end(), 1);
const int sB = std::count(b.begin(), b.end(), 1);
if (a == b) {
Yes();
} else if (sA != sB) {
No();
} else if (sA == 1 && (a.front() != b.front() || a.back() != b.back())) {
No();
} else {
Yes();
}
}
return 0;
}
ARC203C Destruction of Walls
- \(K < H +W - 2\):显然答案为 \(0\)。
- \(K = H + W - 2\):答案为 \(\displaystyle \binom{H + W - 2}{H - 1}\)。
- \(K = H + W - 1\):就是在正常走的基础上额外选一条,答案为 \(\displaystyle \binom{H + W - 2}{H - 1} \binom{2 (H - 1) (W - 1)}{1}\)。
- \(K = H + W\):有两种情况。
- 走一条长度为 \(H + W - 2\) 的路径:在正常走的基础上额外选两条,然后加上额外边构成一个小正方形的情况会算两遍,这部分可以删掉小正方形后计数,然后把小正方形加上去,答案为 \(\displaystyle \binom{H + W - 2}{H - 1} \binom{2 (H - 1) (W - 1)}{2} - \binom{H + W - 4}{H - 2}(H + W - 3)\)。
- 走一条长度为 \(H + W\) 的路径:也就是说要额外往上或往左走一步。考虑这一步的前后两步一定是另一个方向的,可以删掉这三步之后计数,最后加进去,答案为 \(\binom{H + W - 2}{H + 1}(H - 1) \binom{H + W - 2}{W + 1}(W - 1)\)。
int main() {
#ifdef LOCAL
freopen("!in.in", "r", stdin);
freopen("!out.out", "w", stdout);
#endif
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int T;
std::cin >> T;
while (T --) {
int n, m, k;
std::cin >> n >> m >> k;
if (k < n + m - 2) {
std::cout << 0 << '\n';
} else if (k == n + m - 2) {
std::cout << comb.binom(n + m - 2, n - 1) << '\n';
} else if (k == n + m - 1) {
Z ans = comb.binom(n + m - 2, n - 1);
ans *= 2LL * (n - 1) * (m - 1);
std::cout << ans << '\n';
} else {
Z ans = comb.binom(n + m - 2, n - 1);
ans *= 1LL * (n - 1) * (m - 1);
ans *= 2LL * (n - 1) * (m - 1) - 1;
ans -= comb.binom(n + m - 4, n - 2) * (n + m - 3);
ans += comb.binom(n + m - 2, n + 1) * (n - 1);
ans += comb.binom(n + m - 2, m + 1) * (m - 1);
std::cout << ans << '\n';
}
}
return 0;
}
ARC203D Insert XOR
肯定是要变成删数的,有这样几种合法的操作:
- 将 \(\texttt{0}\) 的连续段长度对 \(2\) 取 \(\min\)。
- 若 \(\texttt{1}\) 的连续段和 \(\texttt{0}\) 相邻,那么连续段长度对 \(1\) 取 \(\min\)。
- \(\texttt{101}\) 子串缩成 \(\texttt{11}\) 子串。
分析可以得到,若串是全 \(\texttt{1}\) 串,那么答案为 \(n\);否则需要先保留开头结尾的 \(\texttt{0}\) 段(对 \(2\) 取 \(\min\)),删掉剩余的长度为 \(1\) 的 \(\texttt{0}\) 段,其余的 \(\texttt{1}\) 段会贡献 \(1\),\(\texttt{0}\) 段会贡献 \(2\)。
对于 \(1\) 的段,我们直接点边容斥;对于 \(0\) 的段,可以把 \(\texttt{000}\) 这样的结构看成边,然后容斥,这样得到的结果就是正确的贡献。这样就能得到局部的贡献系数。
时间复杂度线性。
int main() {
#ifdef LOCAL
freopen("!in.in", "r", stdin);
freopen("!out.out", "w", stdout);
#endif
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int n;
std::cin >> n;
std::vector<int> a(n);
for (int i = 0; i < n; i ++) {
std::cin >> a[i];
}
auto f = [&](int i) {
if (i <= 0 || i >= n) {
return 0;
}
if (a[i - 1] == 1 && a[i] == 1) {
return -1;
}
if (i >= n - 1) {
return 0;
}
if (a[i - 1] == 0 && a[i] == 0 && a[i + 1] == 0) {
return -1;
}
if (a[i - 1] == 1 && a[i] == 0 && a[i + 1] == 1) {
return -2;
}
return 0;
};
int ans = n, cnt = 0;
for (int i = 0; i < n; i ++) {
ans += f(i);
cnt += !a[i];
}
int q;
std::cin >> q;
while (q --) {
int i;
std::cin >> i;
-- i;
ans -= f(i - 1);
ans -= f(i);
ans -= f(i + 1);
cnt -= !a[i];
a[i] ^= 1;
ans += f(i - 1);
ans += f(i);
ans += f(i + 1);
cnt += !a[i];
std::cout << (cnt ? std::max(ans, 2) : n) << '\n';
}
return 0;
}
ARC203E Tile Grid with One Hole
先不考虑 \(N, M\),找一下能被完全覆盖的必要条件。
记 \(f_i\) 表示第 \(i\) 行还剩多少个格子没有被覆盖,初始 \(f_r = W - 1, f_i = W\)。此时覆盖一个 \(1 \times L\) 的横向矩形就相当于对 \(f\) 单点减 \(L\);覆盖一个 \(L \times 1\) 的纵向矩形就相当于对 \(f\) 的一个长为 \(L\) 的区间减 \(1\)。我们想使用这两种操作使得 \(f\) 全变成 \(0\)。
在 \(\operatorname{mod} L\) 意义下考虑,记 \(d_i = (f_i - f_{i - 1}) \bmod L\),这样覆盖横向矩形就不会产生影响,覆盖纵向矩形的影响就是 \(d_i \leftarrow d_i - 1, d_{i + L} \leftarrow d_{i + L} + 1\)。目的是使用这个操作使得 \(d\) 都变成 \(0\)。
将下标 \(\operatorname{mod} L\) 相同的位置划分成等价类,注意到操作不会改变同一个等价类的和,所以就是要每个等价类和为 \(0\)。
注意到 \(d\) 初始只有四个位置是有值的:\(d_1 = W, d_r = -1, d_{r +1} = 1, d_{H + 1} = -W\),而 \(r\) 和 \(r + 1\) 一定不是同一个等价类的,那么只有两种情况:
- \(r\) 和 \(1\) 处于同一个等价类,\(r + 1\) 和 \(H + 1\) 处于同一个等价类,\(W - 1 \equiv 0 \pmod L\)。
- \(r + 1\) 和 \(1\) 处于同一个等价类,\(r\) 和 \(H + 1\) 处于同一个等价类,\(W + 1 \equiv 0 \pmod L\)。
列的方向也是同理的,这样就得到了存在合法的覆盖的必要条件:
- \(H \equiv W \equiv r \equiv c \equiv 1 \pmod L\)。
- \(H \equiv W \equiv -1 \pmod L, r \equiv c \equiv 0 \pmod L\)。
对这两种情况的构造分别讨论。
\(H \equiv W \equiv r \equiv c \equiv 1 \pmod L\)
首先需要把 \(d_{r + 1}\) 位置的 \(1\) 和 \(d_{H + 1}\) 位置的 \(-1\) 消掉,这个只需要依次在 \(r + 1, r + L + 1, \cdots, H + 1\) 这些位置操作即可,需要 \(\displaystyle \frac{H - r}{L}\) 个纵向矩形。
然后需要把 \(d_1\) 位置的 \(1\) 和 \(d_r\) 位置的 \(-1\) 消掉,这个只需要依次操作 \(1, L + 1, \cdots, r\) 即可,需要 \(\displaystyle \frac{r - 1}{L}\) 个纵向矩形。
也就是说我们至少需要 \(\displaystyle \frac{H - 1}{L}\) 个纵向矩形才能将所有的 \(d\) 变成 \(0\),同时后面覆盖纵向矩形的时候覆盖的次数一定是 \(L\) 的倍数,这样才能保证 \(d\) 全是 \(0\)。
横向矩形是同理的,这样我们就得到了有解的必要条件:\(\begin{cases} N \equiv \frac{W - 1}{L} \pmod L \\ M \equiv \frac{H - 1}{L} \pmod L \end{cases}\)。
事实上这也是充要条件,构造的话可以根据上面所说的必需的矩形得到(红色的表示扣掉的位置,蓝色和绿色分别表示横向和纵向的矩形,\(L \times L\) 的橙色矩形中可以填 \(L\) 个横向矩形或 \(L\) 个纵向矩形):
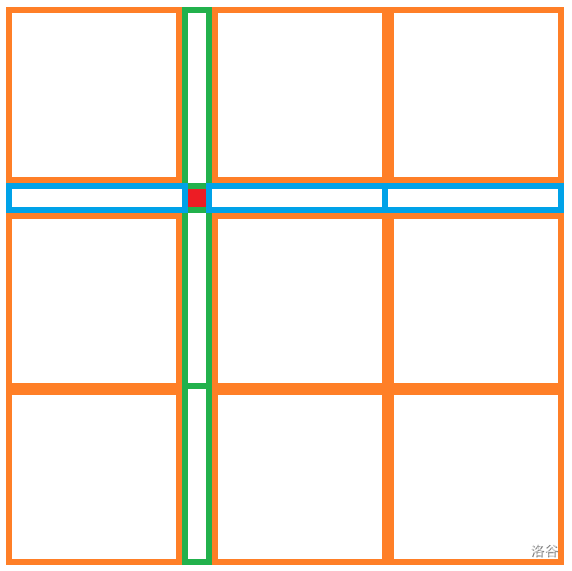
蓝色和绿色的部分分别需要 \(\displaystyle \frac{H - 1}{L}\) 个纵向矩形和 \(\displaystyle \frac{W - 1}{L}\) 个横向矩形,剩余的 \(N, M\) 可以从橙色的部分调整。
\(H \equiv W \equiv -1 \pmod L, r \equiv c \equiv 0 \pmod L\)
同样地,消掉 \(d_1\) 和 \(d_{r + 1}\) 的值需要 \(\displaystyle \frac{r}{L} \cdot (L - 1)\) 个纵向矩形,消掉 \(d_r\) 和 \(d_{H + 1}\) 的值需要 \(\displaystyle \frac{H + 1 - r}{L} \cdot (L - 1)\) 个纵向矩形,也就是说至少需要 \(\displaystyle \frac{(H + 1)(L - 1)}{L}\) 个纵向矩形才能将所有的 \(d\) 变成 \(0\)。
和上一种情况类似,有解的必要条件是:\(\begin{cases} N \equiv \frac{(W + 1)(L - 1)}{L} \pmod L \\ M \equiv \frac{(H + 1)(L - 1)}{L} \pmod L \end{cases}\)。
实际上它也是充要条件,构造也是可以通过上面说的必需的矩形轻松得到:
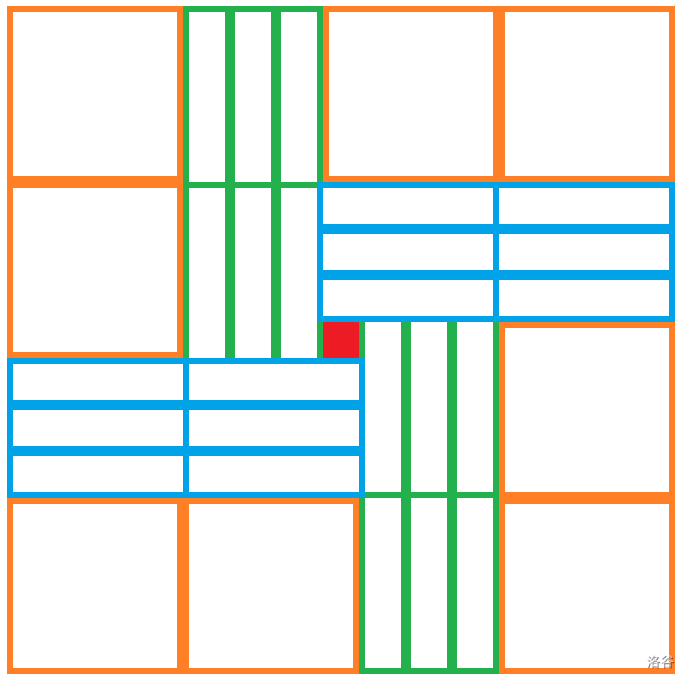
int main() {
#ifdef LOCAL
freopen("!in.in", "r", stdin);
freopen("!out.out", "w", stdout);
#endif
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int T;
std::cin >> T;
while (T --) {
int H, W, L, N, M, r, c;
std::cin >> H >> W >> L >> N >> M >> r >> c;
std::vector<std::pair<int, int>> AB, CD;
AB.reserve(N), CD.reserve(M);
auto work = [&](int x, int y) {
if (N) {
for (int i = x; i < x + L; i ++) {
AB.push_back({i, y});
}
N -= L;
} else if (M) {
for (int j = y; j < y + L; j ++) {
CD.push_back({x, j});
}
M -= L;
} else {
assert(0);
}
};
if (H % L == L - 1 && W % L == L - 1 && r % L == 0 && c % L == 0) {
const int leastN = (W + 1) / L * (L - 1);
const int leastM = (H + 1) / L * (L - 1);
N -= leastN, M -= leastM;
if (N < 0 || N % L != 0 || M < 0 || M % L != 0) {
No();
continue;
}
for (int i = r - L + 1; i < r; i ++) {
for (int j = c; j < W; j += L) {
AB.push_back({i, j});
}
}
for (int i = r + 1; i < r + L; i ++) {
for (int j = 1; j < c; j += L) {
AB.push_back({i, j});
}
}
for (int j = c - L + 1; j < c; j ++) {
for (int i = 1; i < r; i += L) {
CD.push_back({i, j});
}
}
for (int j = c + 1; j < c + L; j ++) {
for (int i = r; i < H; i += L) {
CD.push_back({i, j});
}
}
for (int i = 1; i < r; i += L) {
for (int j = 1; j < c - L; j += L) {
work(i, j);
}
}
for (int i = 1; i < r - L; i += L) {
for (int j = c; j < W; j += L) {
work(i, j);
}
}
for (int i = r + L; i < H; i += L) {
for (int j = 1; j < c; j += L) {
work(i, j);
}
}
for (int i = r; i < H; i += L) {
for (int j = c + L; j < W; j += L) {
work(i, j);
}
}
} else if (H % L == 1 && W % L == 1 && r % L == 1 && c % L == 1) {
const int leastN = (W - 1) / L;
const int leastM = (H - 1) / L;
N -= leastN, M -= leastM;
if (N < 0 || N % L != 0 || M < 0 || M % L != 0) {
No();
continue;
}
for (int j = 1; j < c; j += L) {
AB.push_back({r, j});
}
for (int j = c + 1; j < W; j += L) {
AB.push_back({r, j});
}
for (int i = 1; i < r; i += L) {
CD.push_back({i, c});
}
for (int i = r + 1; i < H; i += L) {
CD.push_back({i, c});
}
for (int i = 1; i < r; i += L) {
for (int j = 1; j < c; j += L) {
work(i, j);
}
}
for (int i = 1; i < r; i += L) {
for (int j = c + 1; j < W; j += L) {
work(i, j);
}
}
for (int i = r + 1; i < H; i += L) {
for (int j = 1; j < c; j += L) {
work(i, j);
}
}
for (int i = r + 1; i < H; i += L) {
for (int j = c + 1; j < W; j += L) {
work(i, j);
}
}
} else {
No();
continue;
}
assert(N == 0 && M == 0);
Yes();
for (auto [x, y] : AB) {
std::cout << x << ' ' << y << '\n';
}
for (auto [x, y] : CD) {
std::cout << x << ' ' << y << '\n';
}
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号