让回归模型不再被异常值"带跑偏"，MSE和Cauchy损失函数在噪声数据环境下的实战对比

在机器学习的回归分析中，损失函数的选择对模型性能具有决定性影响。均方误差（MSE）作为经典的损失函数，在处理干净数据时表现优异，但在面对包含异常值的噪声数据时，其对大误差的二次惩罚机制往往导致模型参数估计产生显著偏差。本文通过实证研究，系统比较了MSE损失函数和Cauchy损失函数在线性回归中的表现，重点分析了两种损失函数在噪声数据环境下的差异。研究结果表明，Cauchy损失函数通过其对数惩罚机制有效降低了异常值的影响，在处理含噪声数据时展现出更强的稳定性。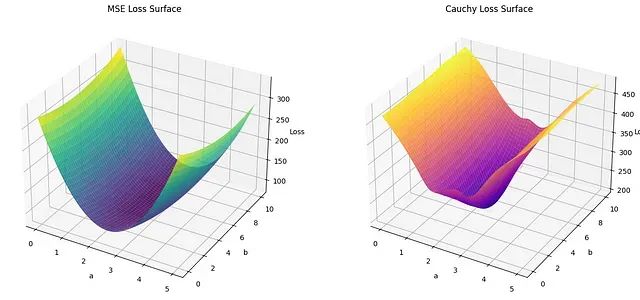

理论基础

均方误差（MSE）损失函数

均方误差损失函数是回归问题中最为常用的损失函数，其数学定义为：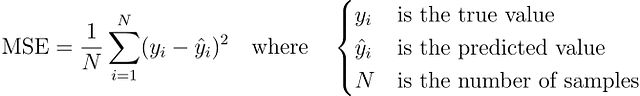

MSE损失函数的优势在于其良好的数学性质。首先，MSE函数处处可微，便于使用基于梯度的优化算法进行参数更新。其次，平方项的引入确保了较大误差获得相应的高权重，驱动模型向更高精度的方向优化。此外，MSE损失函数具有凸函数性质，保证了优化过程能够收敛到全局最优解。

然而，MSE损失函数的主要局限性在于其对异常值的高度敏感性。由于采用二次惩罚机制，远离回归线的数据点会产生较大的平方误差，从而在损失函数中占据主导地位。这种特性使得模型参数估计容易被异常值所"拖拽"，偏离真实的数据分布特征，特别是在处理包含噪声或异常值的实际数据时表现尤为明显。

Cauchy损失函数

Cauchy损失函数属于鲁棒性损失函数家族，其设计目标是降低模型对异常值的敏感性。该损失函数基于Cauchy分布（也称为Lorentz分布）的概率密度函数，其数学表达式为：

其中，δ为尺度参数，控制损失函数的形状和对异常值的容忍度。

Cauchy损失函数的核心优势在于其对数惩罚机制。与MSE的二次增长不同，Cauchy损失函数在残差增大时呈现对数增长特性，这意味着大残差虽然仍会受到惩罚，但其影响程度相对有限。这种特性使得模型在面对异常值时能够保持相对稳定的参数估计，避免被极端值过度影响。

参数δ的选择对Cauchy损失函数的性能具有重要影响。较小的δ值使得损失函数对残差变化更为敏感，而较大的δ值则增强了模型对异常值的容忍度。在实际应用中，δ值通常需要根据数据特性和问题需求进行调整。

 

https://avoid.overfit.cn/post/0db1639503ed43cba8f53b5e8b3ad8f9