[NOI2010][bzoj2005] 能量采集 [欧拉函数+分块前缀和优化]

题面：

传送门

思路：

稍微转化一下，可以发现，每个植物到原点连线上植物的数量，等于gcd(x,y)-1，其中xy是植物的横纵坐标

那么我们实际上就是要求2*sigma(gcd(x,y))-n*m了

又有某不知名神奇定理：一个数的所有因子的phi之和等于这个数本身，其中phi是欧拉函数

因此题目转化为求如下：

 

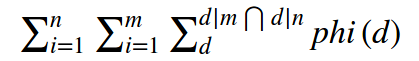
我们把式子变个型，就成了如下式子：

然后一个前缀和优化，O(n+sqrt(n))解决

Code：

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<algorithm>
 4 #include<cstring>
 5 #define ll long long
 6 using namespace std;
 7 inline ll read(){
 8     ll re=0,flag=1;char ch=getchar();
 9     while(ch>'9'||ch<'0'){
10         if(ch=='-') flag=-1;
11         ch=getchar();
12     }
13     while(ch>='0'&&ch<='9') re=(re<<1)+(re<<3)+ch-'0',ch=getchar();
14     return re*flag;
15 }
16 ll phi[100010],pri[100010],cnt,pre[100010];
17 void init(){
18     phi[1]=pre[1]=1;ll i,j,k;
19     for(i=2;i<=100010;i++){
20         if(!phi[i]) phi[i]=i-1,pri[++cnt]=i;
21         for(j=1;(j<=cnt)&&(i*pri[j]<=100010);j++){
22             if(i%pri[j]) phi[i*pri[j]]=phi[i]*(pri[j]-1);
23             else{phi[i*pri[j]]=phi[i]*pri[j];break;}
24         }
25         pre[i]=pre[i-1]+phi[i];
26 //        if(i<=10) cout<<"phi "<<i<<" "<<phi[i]<<"\n";
27     }
28 }
29 ll n,m;ll ans;
30 int main(){
31     init();ll i,j;
32     n=read();m=read();
33     if(n>m) swap(n,m);
34     for(i=1;i<=n;i=j+1){
35         j=min(n/(n/i),m/(m/i));
36         ans+=(ll)(n/i)*(m/i)*(pre[j]-pre[i-1]);
37     }
38     printf("%lld\n",ans*2-n*m);
39 }

 

 

 

∑ni=1∑mi=1∑d|m⋂d|ndphi(d)

∑ni=1∑mi=1∑d|m⋂d|ndphi(d)

posted @ 2018-03-01 22:22  dedicatus545  阅读(221)  评论(0)  编辑  收藏  举报