树状数组与线段树

树状数组

树状数组：O(logn)

操作：1、给某个位置上的数加上一个数 (单点修改)

2、求某一个前缀和 (区间查询)

支持修改和查询同时进行，是在线的

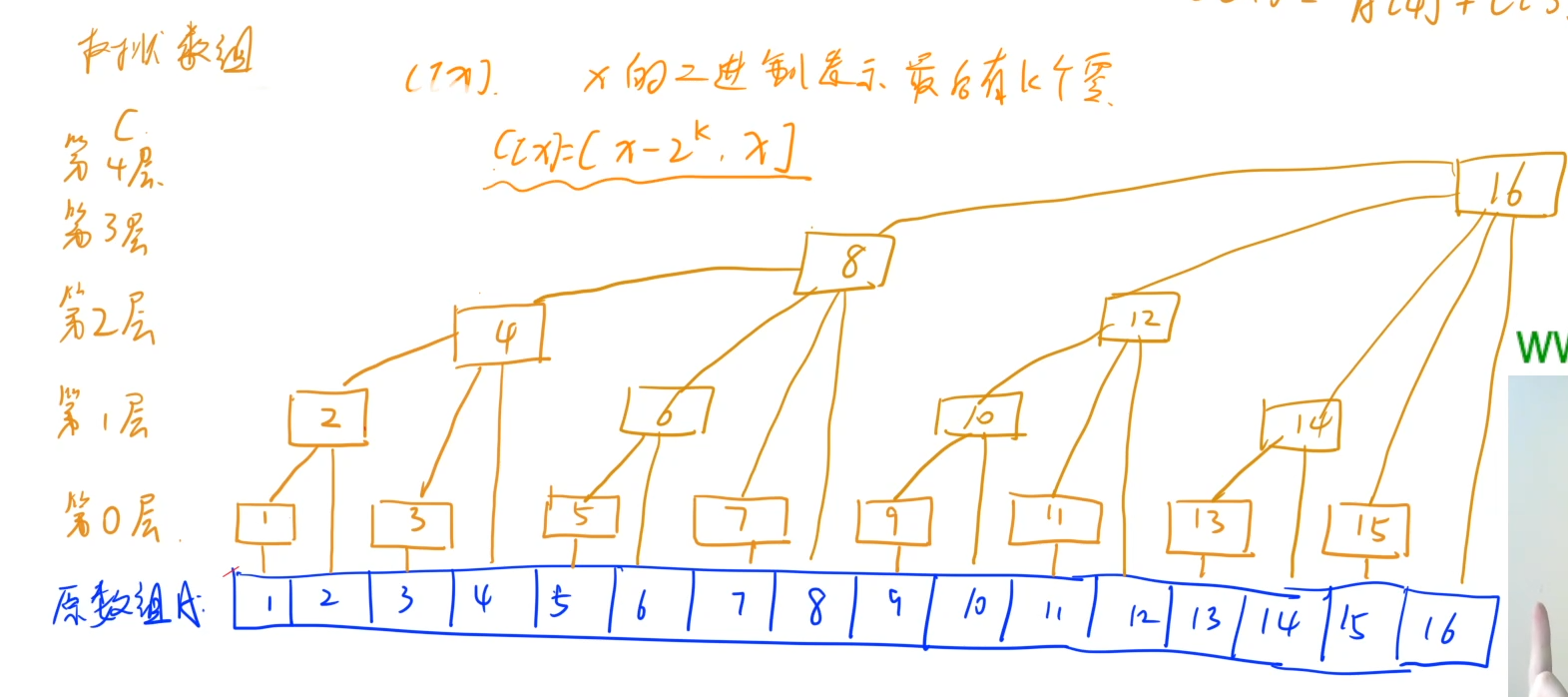
树状数组下标 所在的层次：x的二进制最后有几个0

C[x]表示的数的范围：\((x - 2 ^k, x] = (x - lowbit(x), x]\)

如 \(6=(0110)_2\)， 末尾有1个0, 则C[6]表示的和为\((4,6]\)。

求前缀和，递推把包括的子区间的和都加起来

// 前 x 个数的和
int query(int x) {
    int res = 0;
	for(int i = x; i > 0; i -= lowbit(i))	
        res += C[i];
}

在某个位置上加上某个数\(v\)

// 更新x位置上连接的父节点数组C的的值
void add(int x, int v) {
    for(int i = x; i <= n; i+= lowbit(i))
    C[i] += v;
}

当初始化原数组时候，直接在某个位置上加上原数组位上对应的值。

for(int i = 1;i <= n; i++) {
    int x;
    cin >> x;
    add(i, x);
}

线段树

操作

1、单点修改 O(logn)

2、区间查询 O(logn)

3、区间修改 --> 懒标记(暂时不学)

方法

0、线段树节点

struct Node {
    int l, r;
    int sum;
}tr[N * 4];

1、pushup： 用子节点信息更新当前节点信息

void pushup(int u) {
    tr[u].sum = tr[u << 1].sum + tr[u << 1 + 1].sum;
}

2、bulid： 在一段区间上初始化线段树

void bulid(int u, int l, int r) {
    if(l == r)	tr[u].sum = {l, r, w[r]};
    else {
        tru[u] = {l, r};
        int mid =  l + r >> 1;
        bulid(u << 1 , l, mid), bulid(u << 1 + 1, mid+1, r);
        pushup(u); // 合并两个子树到根节点
    }
}

3、modify： 修改

void modify(int u, int x, int v) {
    if(tr[u].l == tr[u].r)	tr[u].sum += v; // 修改单个节点
    else {
        int mid = tr[u].l + tr[u].r >> 1;
        if(x <= mid)	modify(u << 1, x, v); // 递归左子树
        else	modify(u << 1 + 1, x, v); // 递归右子树
        pushup(u); // 用左右子树更新根节点
    }
}

4、query： 查询

int query(int u, int l, int r) {
    if(tr[u].l >= l && tr[u].l <= r)	return tr[u].sum; // 查询的区间包含线段树节点的区间
    int mid = tr[u].l + tr[u].r >> 1;
    int sum = 0;
    if(l <= mid)	sum = query(u << 1, l, r);
    if(r > mid)		sum += query(u << 1 + 1, l, r);
}

注意：查询的时候左右子树的区间都取[l,r]的原因是，由于mid的原因，可能最后会多算。比如查询区间\(2-5\) 的和，递归到\([5,7]\)时要查询的区间为\([5,5]\)。那么到了\([5,6]\)要求的就变成了\([5,6]\)，这时候就多算了一个6号节点。