[CQOI2014]数三角形

[CQOI2014]数三角形

题解

这道题传统的题解，是容斥+斜率。。。

但这样写细节很多我没打对

所以就学习了一种特别巧的解法：https://www.luogu.org/blog/scp-d14134/solution-p3166

对于一种三角形ABC,我们发现能完全覆盖它的最小的矩形一定是唯一的，

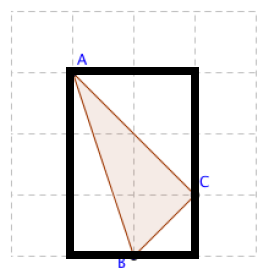
所以反过来，每一种不同的矩形作为完全覆盖△ABC的最小的矩形能覆盖所有种三角形一定是不重复且不遗漏的。

所以可以通过枚举这个矩形来求答案。

那么，怎么求一个长为 i 宽为 j 的矩形MNPQ所覆盖的答案数呢？

首先，如果三角形ABC的顶点都在矩形MNPQ的边上而不是顶点上，因为它是三角形只有三个顶点所以最多只占到了MNPQ的其中三条边，那么第四条边总可以往内缩一点点导致MNPQ不是完全覆盖△ABC的最小的矩形。

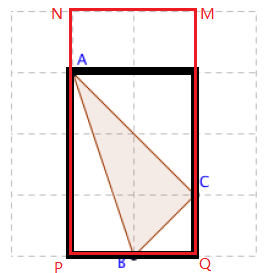
因此三角形ABC至少有一个顶点在MNPQ的顶点上。

于是我们可以分情况讨论一下，

ABC都在顶点上时，显然有4种情况。

有两个点在定点上时，假设A在M上，B在顶点上，有二种小情况

1.B在N或Q上，共有(i - 1) + (j - 1)种情况

2.B在P上，C可以在MNPQ除N、Q、AB线上的其他任意地方，那么AB上共有多少个点呢？

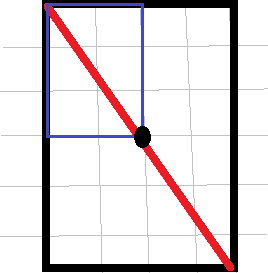
因为格点的坐标都是整数嘛，所以相邻格点的横纵坐标差就应该是  (i / gcd(i,j)) 和 (j / gcd(i,j)) ，总的点数就是 i / (i / gcd(i,j)) - 1 = gcd(i,j) - 1，所以C共有 (i + 1)*(j + 1) - 3 - gcd(i,j) 种情况。

以上二种小情况再乘个2。

有一个点在顶点上时，固定这个点，有(i - 1)*(j - 1)种情况，合计4 * (i - 1)*(j - 1)。

那么一个这样的矩阵的答案数就等于 4∗(i−1)∗(j−1)+2∗[(i−1)+(j−1)+(i+1)∗(j+1)−3−gcd(i,j)]+4

=6*i*j-2*gcd(i,j)

所以算到最后，只用枚举一下矩阵，然后乘上这个数就行。

短短几行：

#include<cstdio>
#define LL long long
using namespace std;
int n,m;
LL ans = 0;
LL gcd(LL a,LL b) {
	return b == 0 ? a : gcd(b,a % b);
}
int main() {
    scanf("%d%d",&n,&m);
    for(int i = 1;i <= n;i ++) {
    	for(int j = 1;j <= m;j ++) {
    		ans += (6ll * i * 1ll*j - 2 * gcd(i,j)) *1ll* (n - i + 1) * 1ll*(m-j + 1);
		}
	}
	printf("%lld\n",ans);
	return 0;
}